The equivalent inductance between points P and Q in figure is :
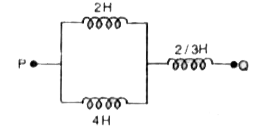
2H
6H
8/3H
4/9H
The correct Answer is:A
Step by step video & image solution for The equivalent inductance between points P and Q in figure is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE - II (DC CIRCUITS)
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE EXERCISE (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW , AC GENERATOR)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE - II (MOTIONAL EMF)
3 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
The equivalent inductance between points P and Q in the figure is :
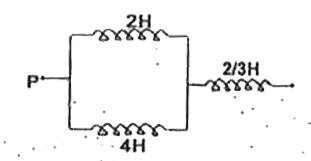
View SolutionThe equivalent inductance between points P and Q in the figure is

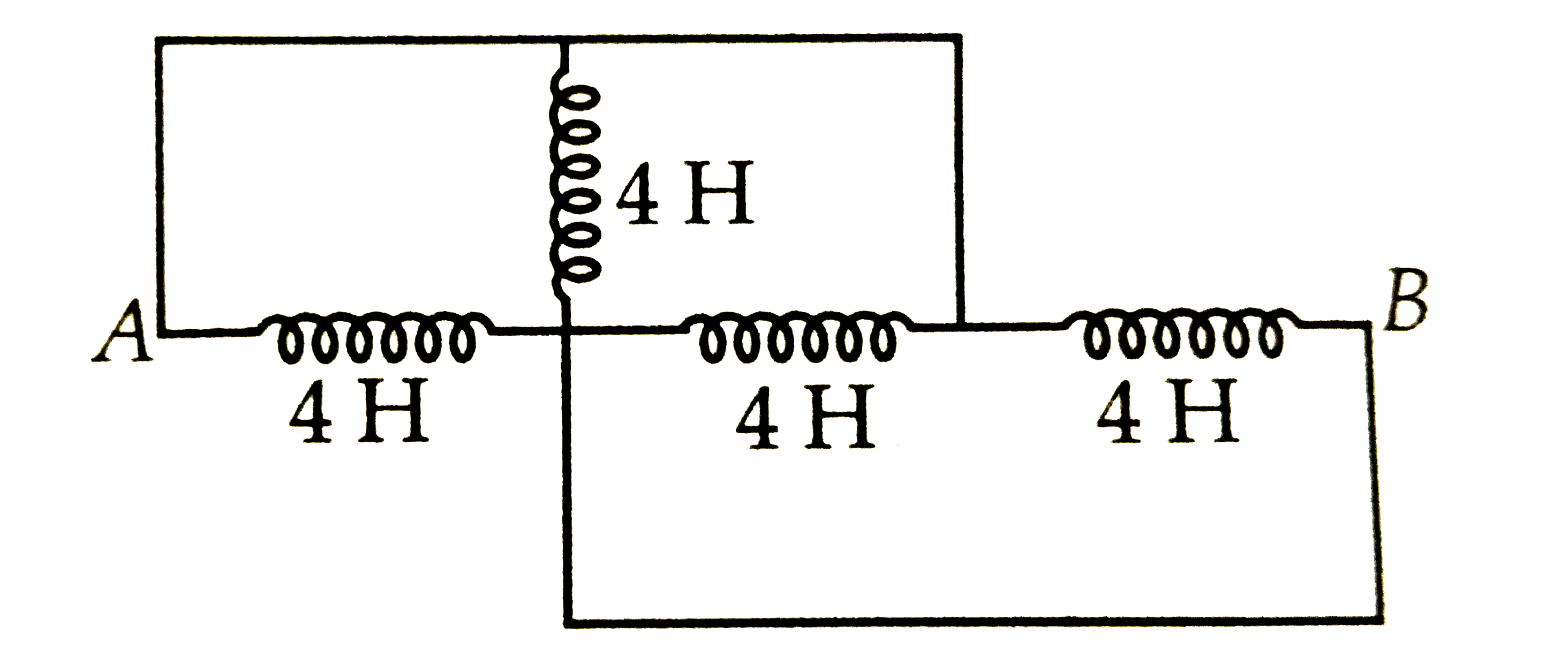
View SolutionThe equivalent inductance between A and B is
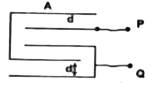
View SolutionThe equivalent capacitance between P and Q in the figure is (area of each plate is A and separation between two consecutive plates is d)
View SolutionThe equivalent resistance between P and Q in the figure is approximately

View SolutionWhat will be the equivalent resistance between points A and B form gives figure ?
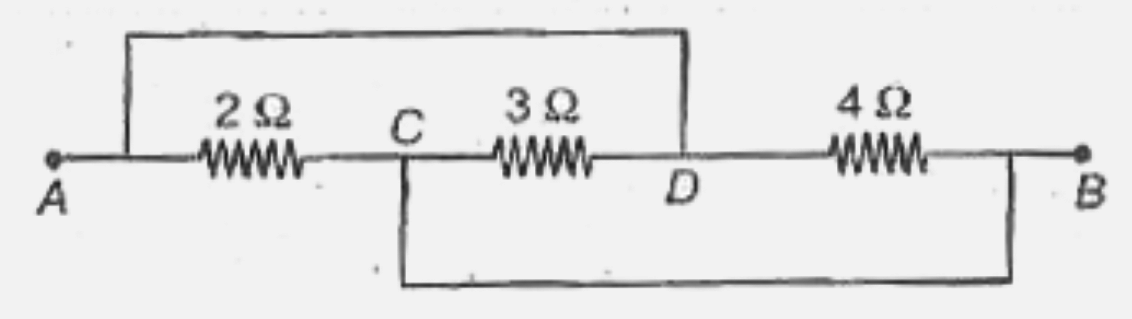
View SolutionWhat will be the equivalent resistance between point A and B from given figure?
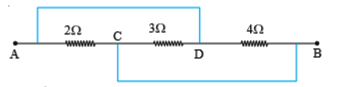
View SolutionFind equivalent capacitance between points A and B shown in figure

View SolutionThe equivalent resistance between the point P and Q in the network given here is equal to (given r=32Ω)
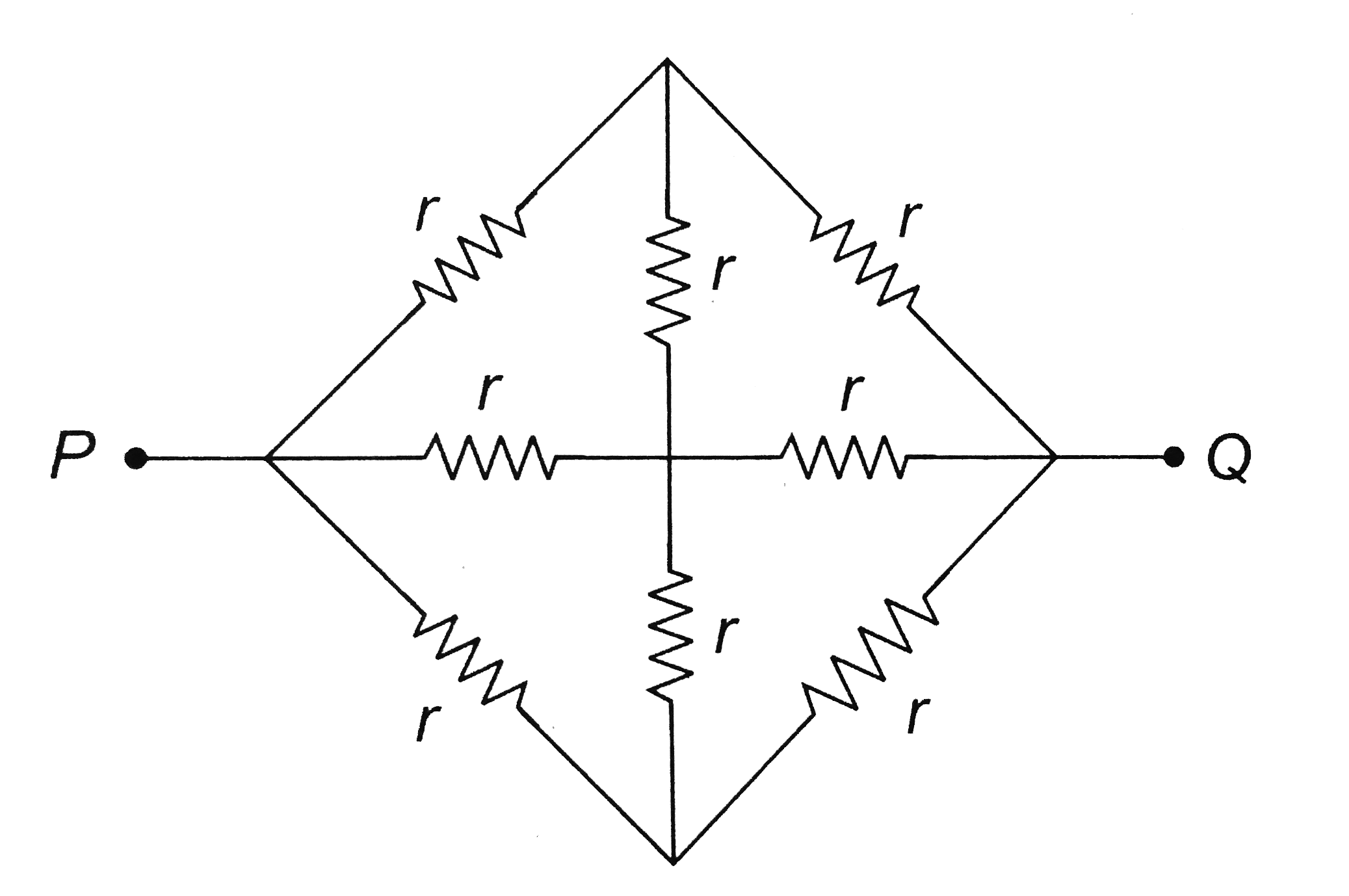
View SolutionThree identical inductors are connected as shown in the figure. At the instant when current in inductor P is increasing at the rate of 0.0320 As−1 then magnitude of induced emf in it is 0.080 V. The equivalent inductance between the points A and B will be
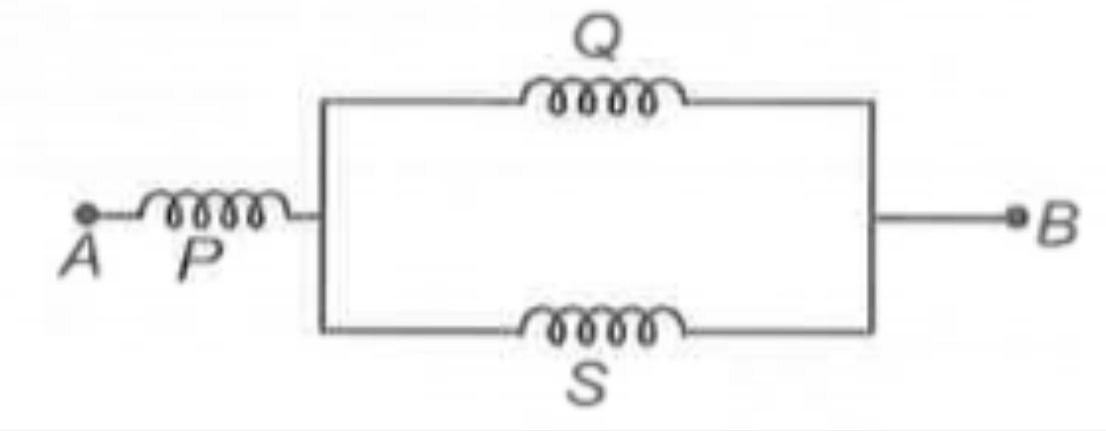
View Solution
