The equivalent resistance between point A and B of an infinite net work of resistances each of 1Ω connected
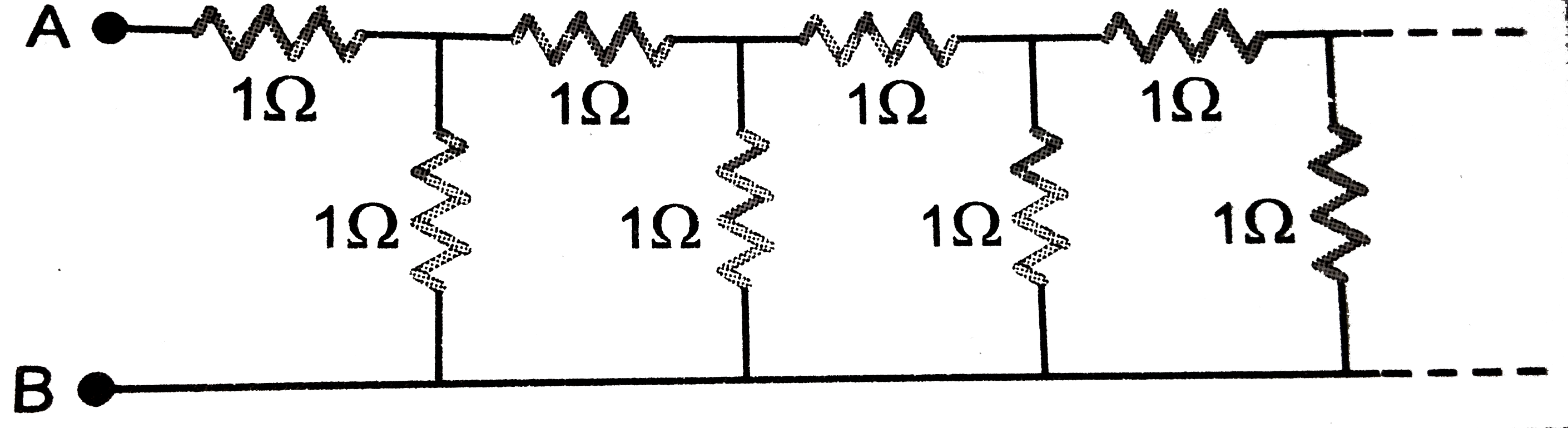
A
infinite
B
2Ω
C
1+√32
D
zero
Video Solution
Text Solution
The correct Answer is:c
Let x be the total resistance of infinite net work of adding connected to point A and B. Therefore adding of one step of resistance in the total resistance x of the network. Therefore equivalent circuit will be total resistance A' and B' is x given by
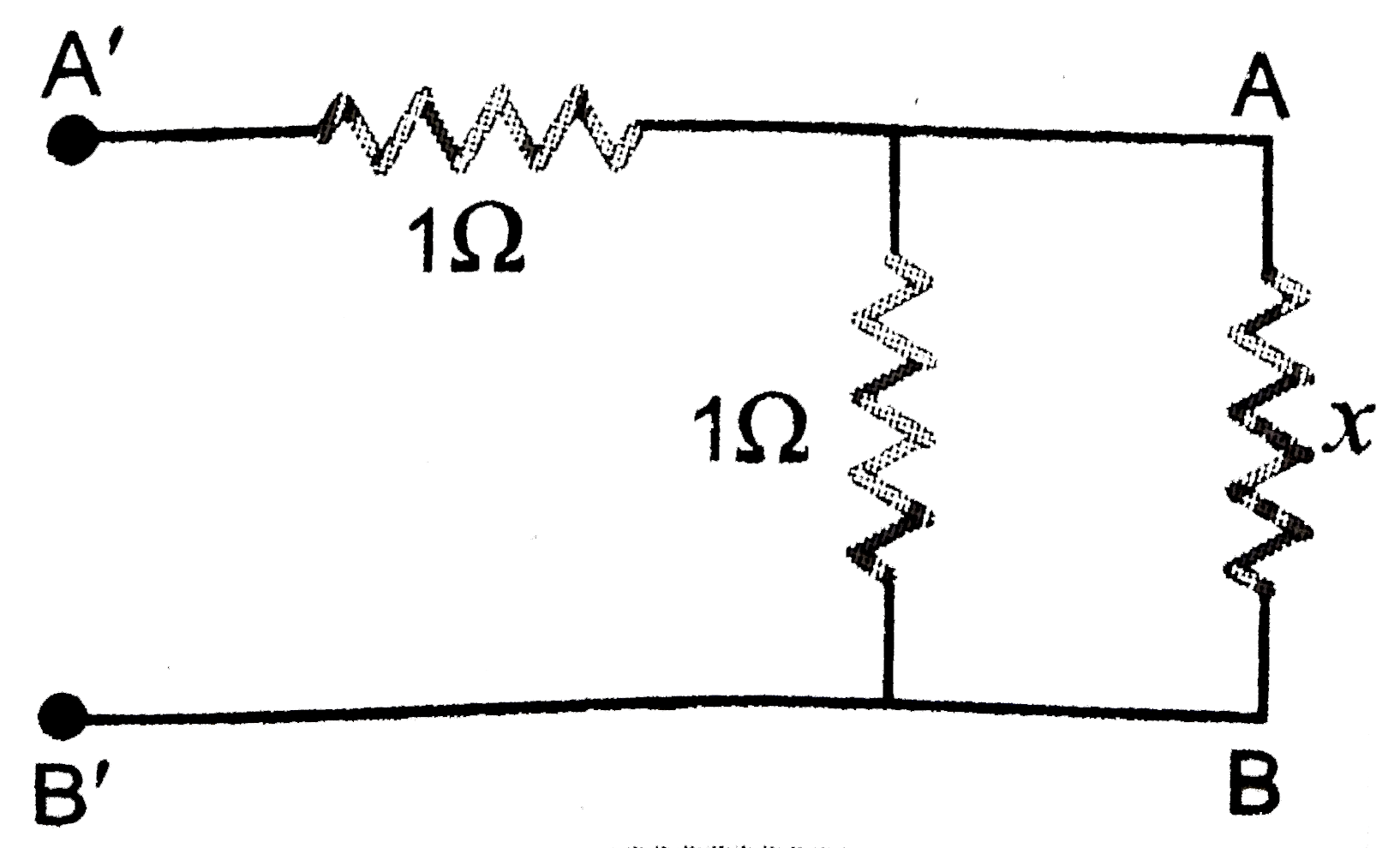
x=1+1×x1+x=1+2x1+x
or x+x2=1+2xorx2−x−1=0
x=1±√52=1+√32
Since since negtive value of R is not possible.
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Jee (main and advance)
4 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Interger Type
2 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Value based
2 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
Knowledge Check
The equivalent resistance between points A and B
 A2ΩB4ΩC1ΩDNone of these
A2ΩB4ΩC1ΩDNone of theseThe equivalent resistance between points A and B
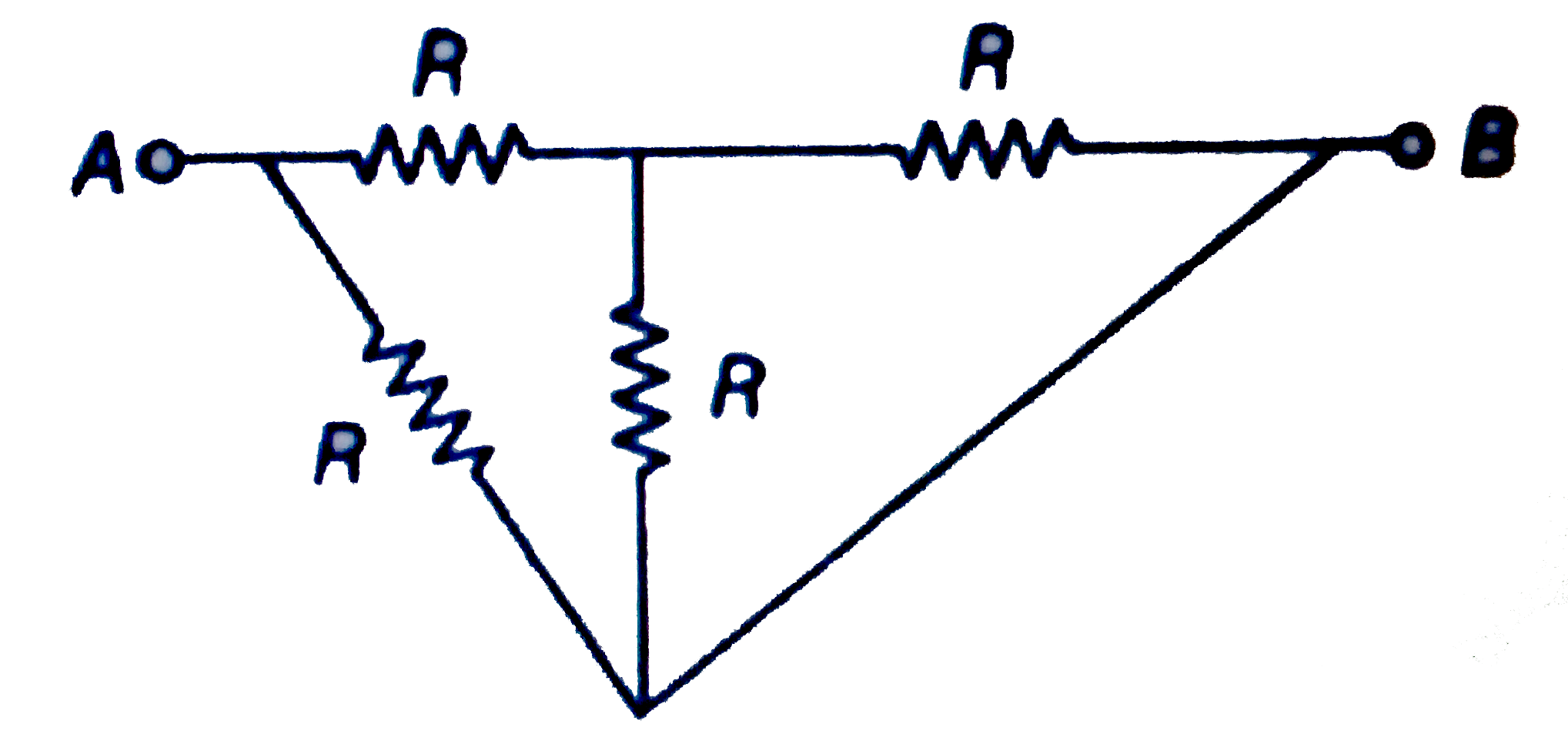 A2RB34RC43RD35R
A2RB34RC43RD35RThe equivalent resistance between points A and B of an infinite network of resistances each of 1Ω connected as shown, is
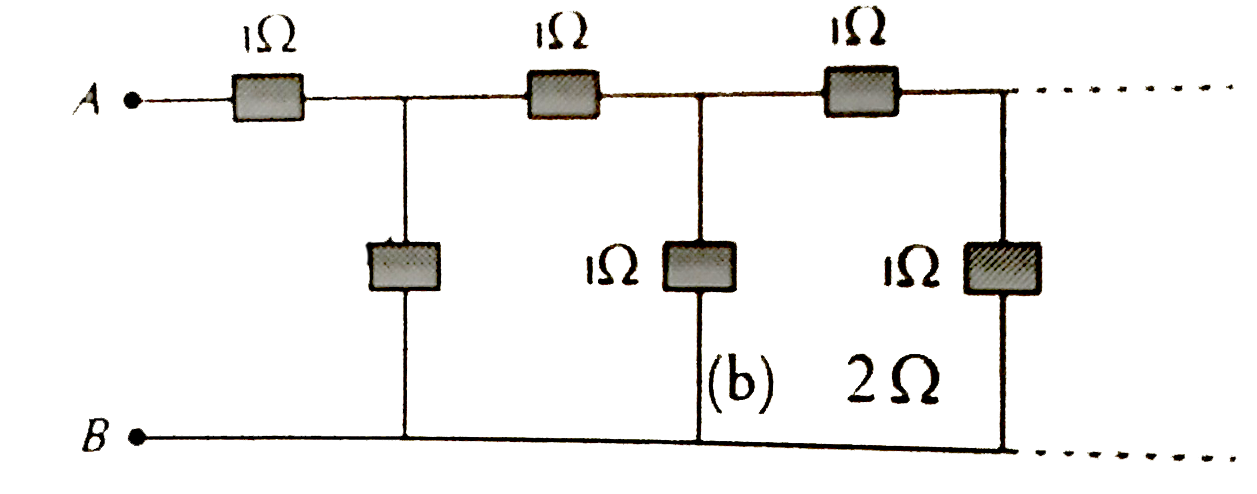 AInfiniteB2ΩC1+√52ΩDZero
AInfiniteB2ΩC1+√52ΩDZero
The equivalent resistance between point A and B of an infinite network of resistance, each of 1Ω, connected as shown, is
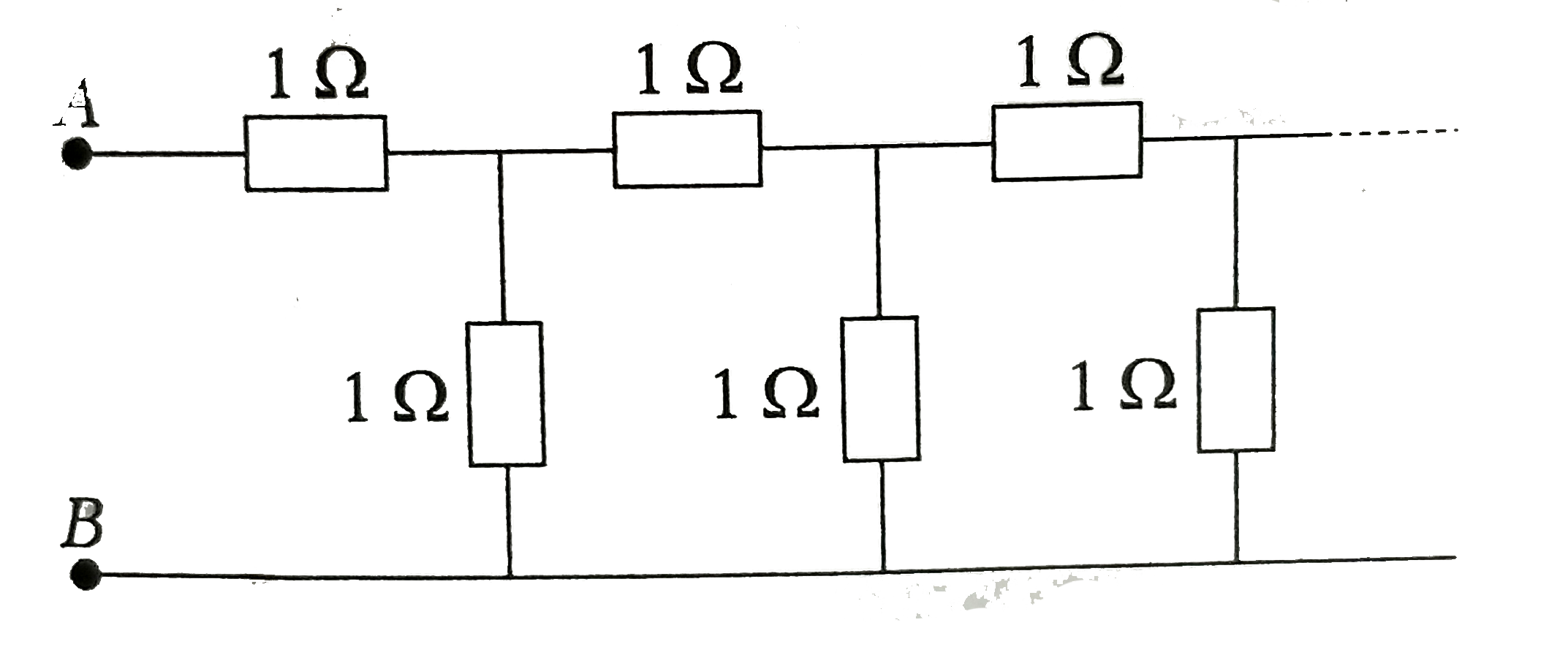
View Solution
The equivalent resistance between points A and B of an infinite network of resistance each of 1Ω connected as shown is
View SolutionThe equivalent resistance between points A and B is

View SolutionThe equivalent resistance between points A and B is

View SolutionThe equivalent resistance between the point A and B is
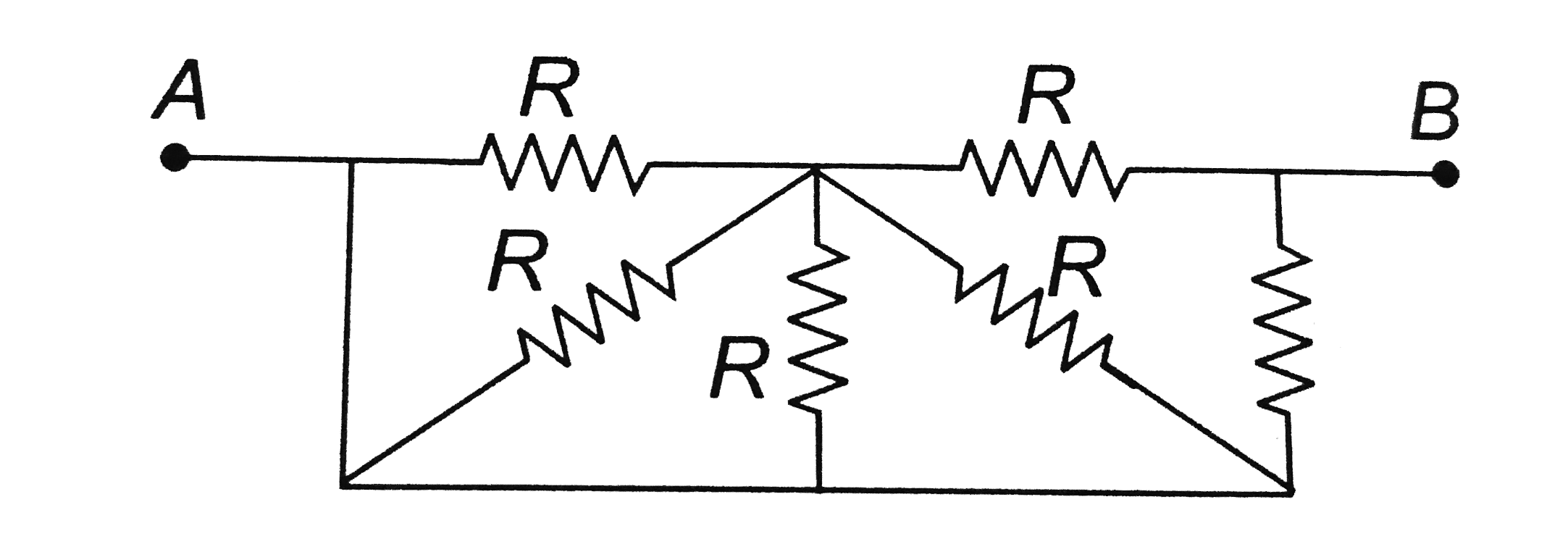
View Solution