The escape velocity form the centre of a unifrom ring of mass M and radius R is :
The correct Answer is:A
Topper's Solved these Questions
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Motion Of Satellite
33 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Problems Based On Mixed Concepts
29 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Gravitational Field And Acceleration Due To Gravity
34 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test
30 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRThe escape velocity of a sphere of mass m from the earth having mass M and radius R is given by
A√2GMRB2√GMRC√2GmMRD√GMRThe total energy of rolling ring of mass m and radius R is
A3/2mv2B1/2mv2Cmv2D5/2mv2
A particle of mass m is placed at a distance R from centre of a uniformly dense thin ring of mass m rand radius R on a axis passing through its centre and perpendicular to its plane. Find the speed of the particle when it reaches at the centre fo the ring due to their mutual gravitation force.
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
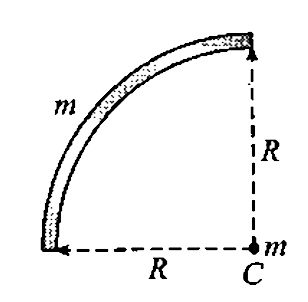
View SolutionThe escape velocity corresponding to a planet of mass M and radius R is 50kms−1. If the planet's mass and radius were 4M and R, respectively, then the corresponding escape velocity would be
View SolutionA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
View SolutionIf ve is the escape velocity of a body from a planet of mass 'M' and radius 'R. Then the velocity of the satellite revolving at height 'h' from the surface of the planet will be
View Solution
