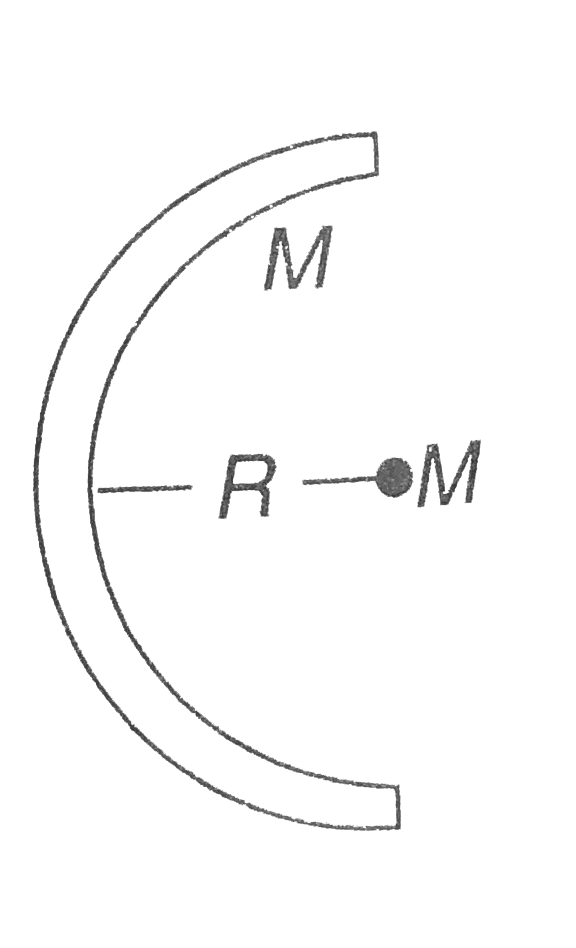
The potential energy of interaction between the semi-circular ring of mass M and radius R, and the particle of mass M placed at the centre of curvature of the semi-circular arc is:
A
−GM2R
B
−2GM2R
C
−GM2πR
D
none of these
Video Solution
Text Solution
The correct Answer is:A
v=−GMMR=−GM2R
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Motion Of Satellite33videos
GRAVITATION
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Problems Based On Mixed Concepts29videos
GRAVITATION
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Gravitational Field And Acceleration Due To Gravity34videos
GRAVITATION
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test30videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
- BOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test29videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR - Question 2 - Select One
The total energy of rolling ring of mass m and radius R is
A3/2mv2B1/2mv2Cmv2D5/2mv2 - Question 3 - Select One
The semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
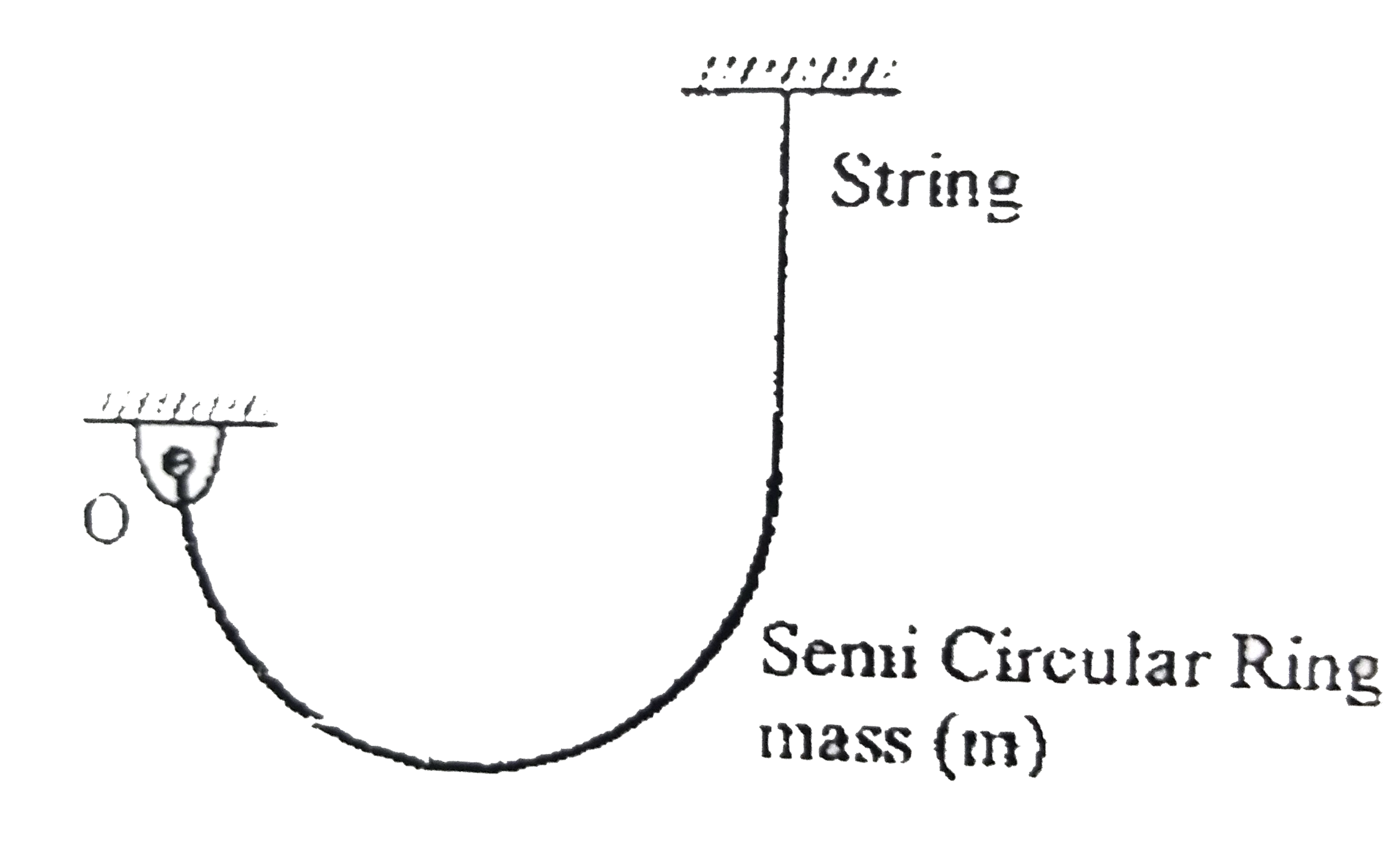 ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.
ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionFind the gravitational potential due to a hemispherical cup of mass M and radius R, at its centre of curvature.
View SolutionFind the gravitational potential due to a hemispherical cup of mass M and radius R, at its centre of curvature.
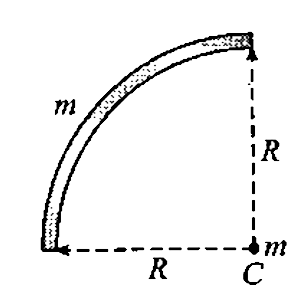
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
 View Solution
View SolutionThe coordinates of centre of mass of the following quarter circular arc is -
 View Solution
View Solution

