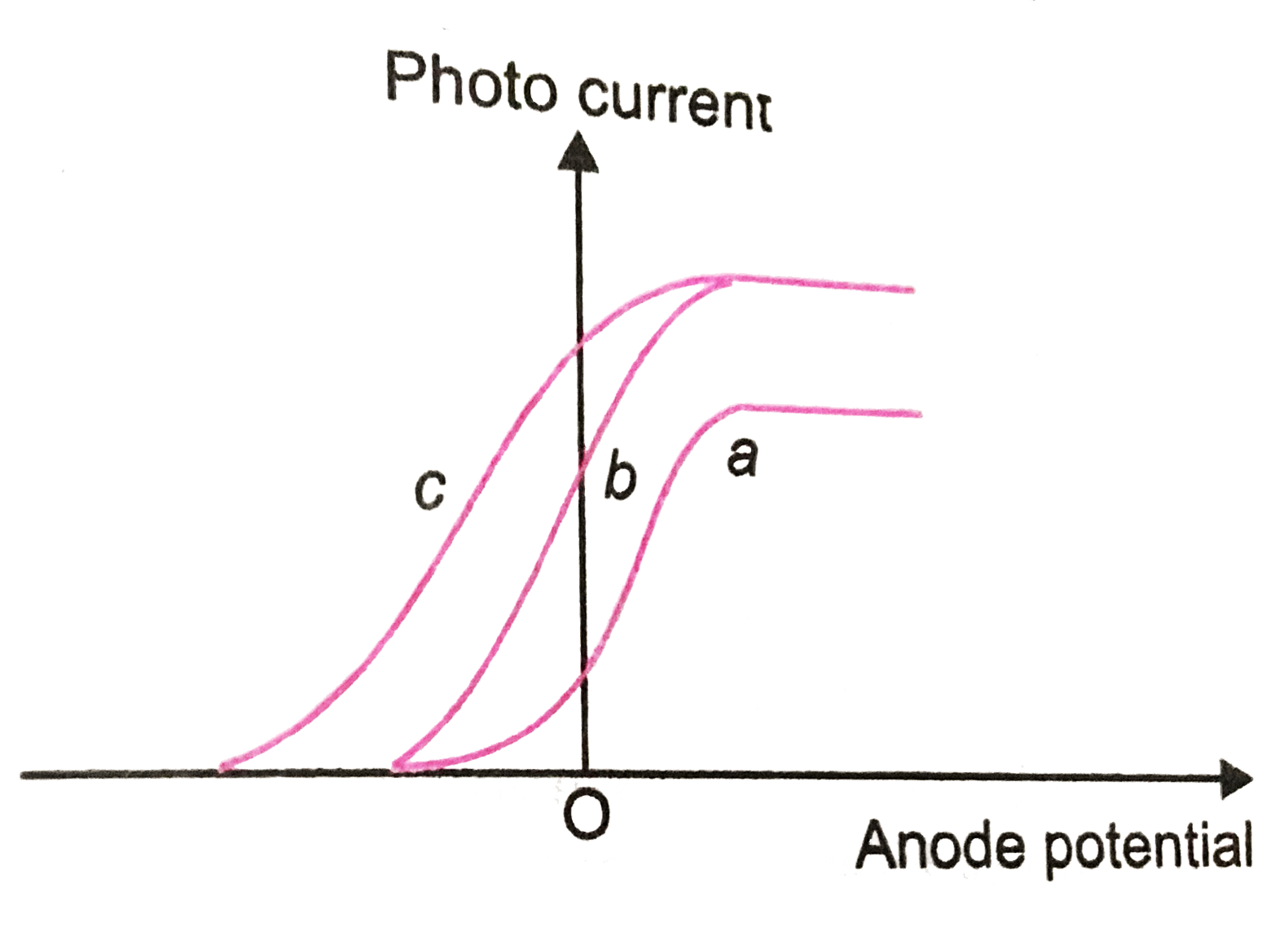
The fig. shows the variation of photon current with anode potential for a photo-sensitive surface for three different radiation. Let Ia,IbandIc be the intensities and fa,fbandfc be the frequency for the curves a,b and c respectively.
va=vbandIa≠Ib
va=vcandIa=Ic
va=vbandIa=Ib
vb=vcandIb=Ic
The correct Answer is:A
(a) : Form the graph, we note that the saturation current is same for curves b and c but different for curve
a. Therefore, intensities of b and c will be equal but different from that of a i.e. Ia≠IbbutIb=Ic. As stopping potential is same for curves a and b, hence va=vb. Thus answer (a) is correct.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Einstein'S Photoelectric Equation : Energy Quantum Of Radiation
23 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Particle Nature Of Light : The Photon
19 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Photoelectric Effect
2 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
The figure shows the variation of photocurrent with anode potential for a photosensitve surface for three different radiations. Let la,lbandlc be the curves a, b and c, respectively

(a) fa=fbandla≠lb (b) fa=fcandla=lc
(c ) fa=fbandla=lb (d) fb=fcandlb=lc
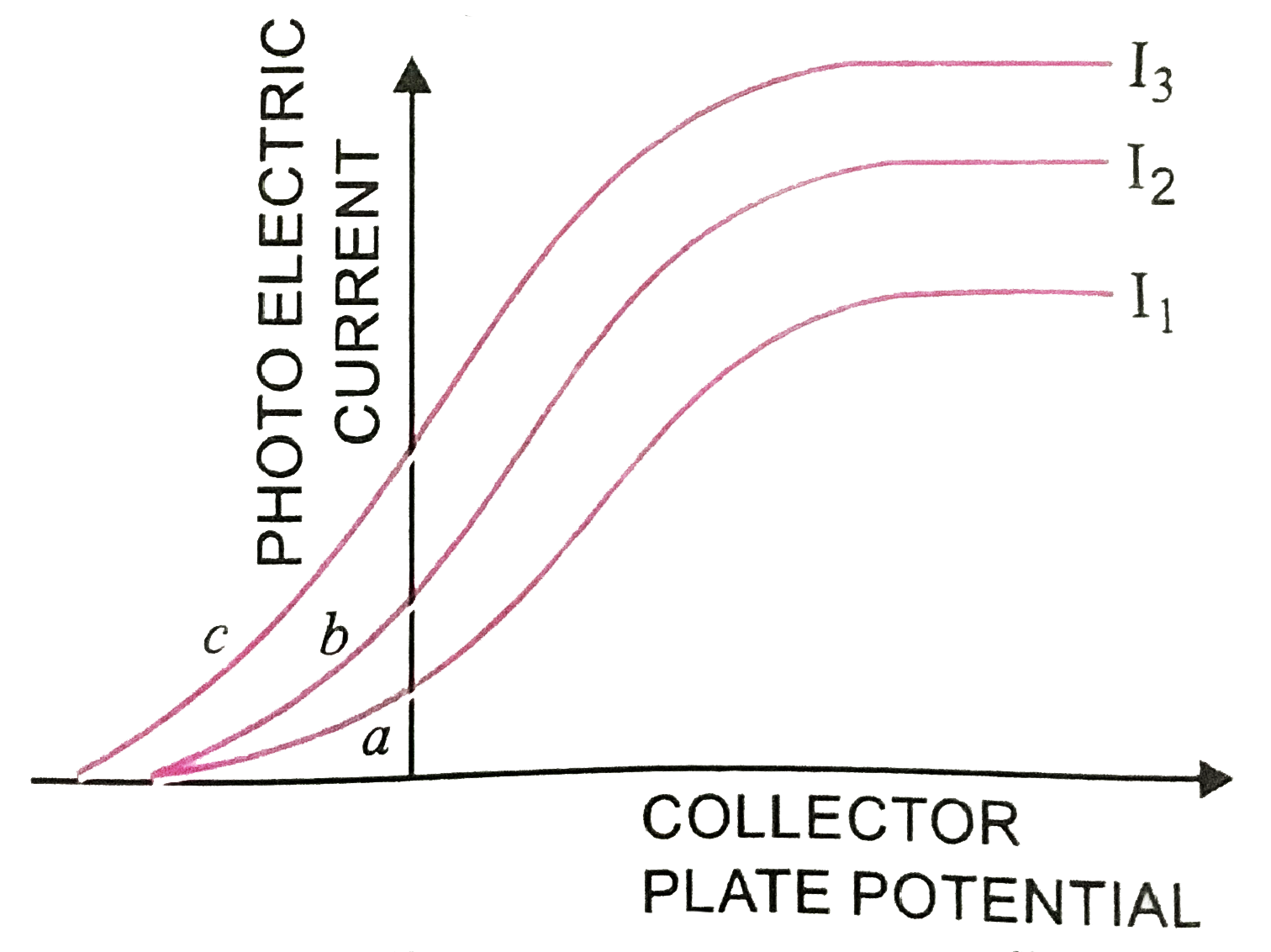
View SolutionThe Fig shows a plot of three curves a, b, c showing the variation of photocurrent versis collector plate potential for the different intensities I1,I2andI3 having frequencies v1,v2andv3 respectively, incident on a photosensitive surface. Point out the two curves for which the incident radiation have same frequency but different intensities.
View Solution
Knowledge Check
In the following figure shows the variation of photocurrent with potential of the collector plate for a photosensitive surface for three different radiations. Let Ia,IbandIc be the intensities and fa,fbandfc be the frequencies for the curves a, b, and c, respectively.
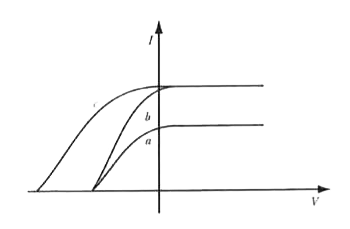 Afa=fbandIa=IbBfa=fcandIa=IcCfa=fbandIa<IbDfa=fcandIb=Ic
Afa=fbandIa=IbBfa=fcandIa=IcCfa=fbandIa<IbDfa=fcandIb=IcThe figure shows a plot of photo current versus anode potential for a photosensitive surface for three different radiations. Which one of the following is a correct statement ?
 ACurves a and b represent incident radiations of different frequencies and different intensitiesBCurves a and b represent incident radiations of the same frequency but no different intensitiesCCurves b and c represent incident radiations of different frequencies and different intensitiesDCurve b and c represent incident radiations of the same frequency having the same intensity
ACurves a and b represent incident radiations of different frequencies and different intensitiesBCurves a and b represent incident radiations of the same frequency but no different intensitiesCCurves b and c represent incident radiations of different frequencies and different intensitiesDCurve b and c represent incident radiations of the same frequency having the same intensityLet I1=∫ba(∫xaf(t)dt)dxandI2=∫ba(b−x)f(x)dx then
AI1=I2BI1=(b−a)+I2CI1=(b−a)I2Dnone of these
Draw suitable graphs to show the variation of photoelectric current with collector plate potential for
(i) a fixed frequency but different intensities I1>I2>I3 of radiation.
(ii) a fixed intensity but different frequencies v1>v2>v3 of radiation.
View SolutionIf f is a bijection and g is the inverse of f; then fog=IB and gof=IA where IA and IB are the identity functions on the sets A and B respectively.
View Solution(i) In a plot of photoelectric current versus anode potential, how does
(a) the saturation current vary with anode potential for incident radiations of different frequencies but same intensity ?
(b) The stopping potential vary for incident radiations of different intensities but same frequency ?
(c) photoelectric current vary for different intensities but same frequency of incident radiations ?
Justify your answer in each case.
(ii) The work function of caesium is 2.14 eV. find (a) the threshold frequency for caesium, and
(b) The wavelength of the incident light if the photocurrent is brought to zero by a stopping potential of 0.60 V.
View Solutionif A, B and C are three such numbers that A divides B and B divides C, then
View SolutionThe graph shows variation of I with f for a series R-L-C network. Keeping L and C constant. If R decreases :-
View Solution
