The figure here shows three cylindrical copper conductors along with their faces areas and lengths. Rank them according to the current through them, greatest first, when the same potential differnce V is placed across their lengths. 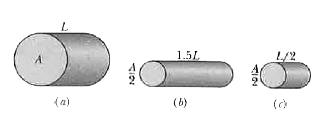
The correct Answer is:a and c tie, then b
Step by step video, text & image solution for The figure here shows three cylindrical copper conductors along with their faces areas and lengths. Rank them according to the current through them, greatest first, when the same potential differnce V is placed across their lengths. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Problems
36 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Single Corret Choice Type)
39 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)
3 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
Figure (a), (b) and (c) show three cylindrical copper conductors alongwith their face areas and length. Which of the conductors will have highest resistance and why?

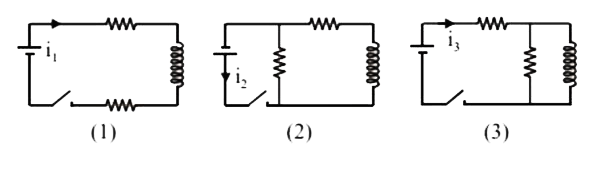
View SolutionThe figure shows three circuit with identical batteries, inductors and resistance. Rank the circuit according to the currents through the battery just after the switch is closed greatest first :
View Solution
Knowledge Check
The figure shows three circuits with identical batteries, inductors and resistance, Rank the circuits according to the currents through the battery just after the switch is closed, greatest first :
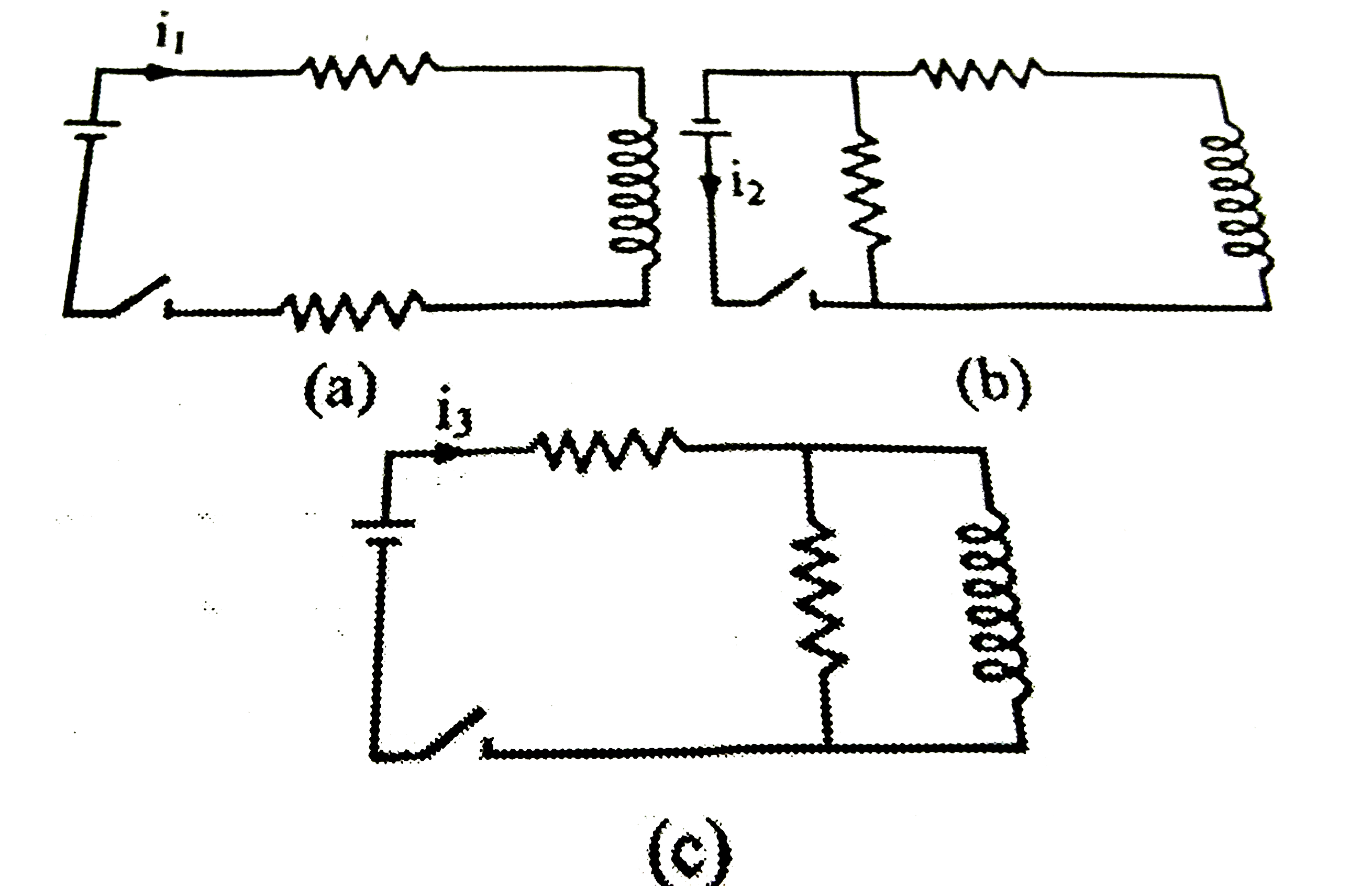 Ai2>i3>i1Bi2>i1>i3Ci1>i2>i3Di1>i3>i2
Ai2>i3>i1Bi2>i1>i3Ci1>i2>i3Di1>i3>i2The figure shows three circuit with identical batteries, inductors, and resistors. Rank the circuit according to the current through the battery (i) just after the switch is closed and (ii) a long time later, greatest first
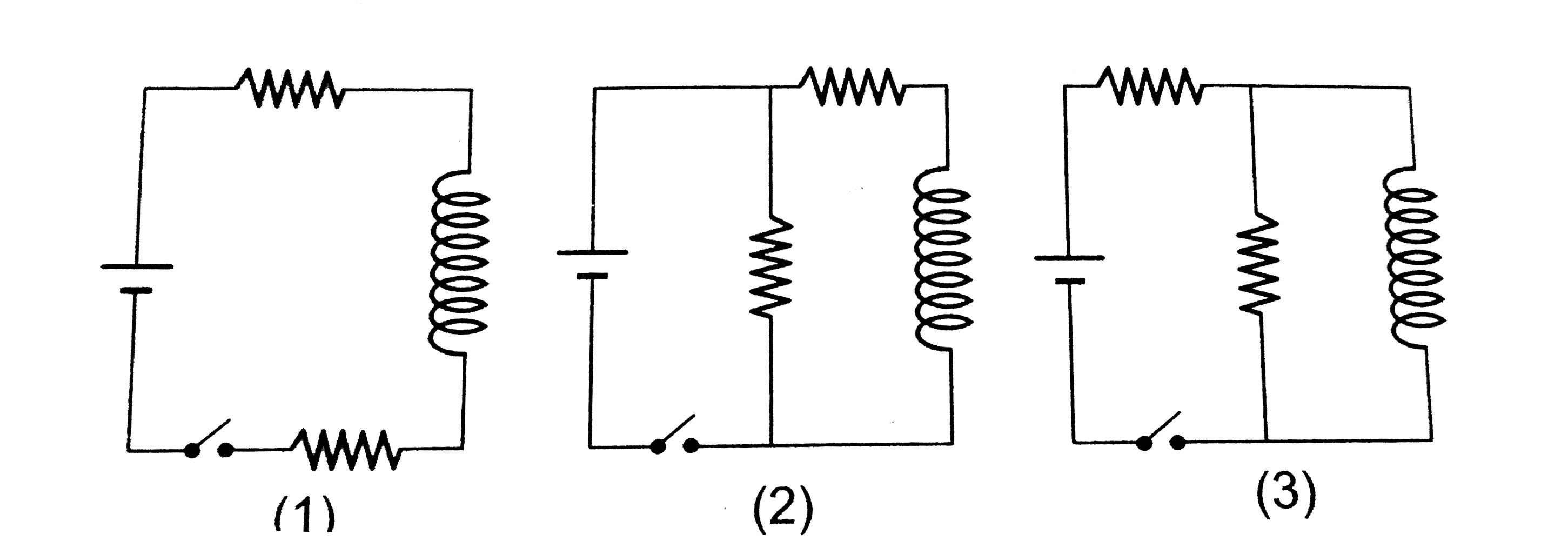 A(i)i2>i3>i1(i1=0)(ii)i2>i3>i1B(i)i2>i3>i1(i1≠0)(ii)i2>i3>i1C(i)i2=i3=i1(i1=0)(ii)i2>i3>i1D(i)i2=i3=i1(i1≠0)(ii)i2>i3>i1
A(i)i2>i3>i1(i1=0)(ii)i2>i3>i1B(i)i2>i3>i1(i1≠0)(ii)i2>i3>i1C(i)i2=i3=i1(i1=0)(ii)i2>i3>i1D(i)i2=i3=i1(i1≠0)(ii)i2>i3>i1The diagrams show three circuits with identical batteries, identical inductors, and identical resistors.
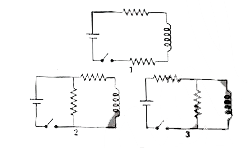
Rank them according to the current through the battery just after the switch is closed from least to greatest.A3,2,1B1,3,2C1,2,3D3,1,2
Two wires A and B are of same metal, have the same area of cross-section and have their lengths in the ratio 2:1. What will be the ratio of currents flowing through them respectively when the same potential difference is applied across the length of each of them ?
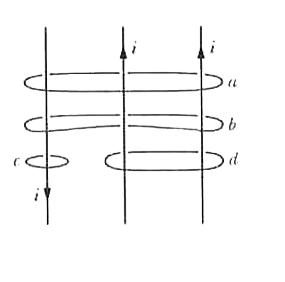
View SolutionThe figure here shows three equal currents i (two parallel and one antiparallel) and four Amperian loops. Rank the loops according to the magnitude of ∮ along each, greatest first.
View SolutionIf R1>R2>Ry rank the three resistance according to (a) the current through them and (b) the potential across them, greatest first.
View SolutionThree resistances 2Ω,3Ω and 4Ω are connected in parallel. The ratio of currents passing through them when a potential difference is applied across its ends will be
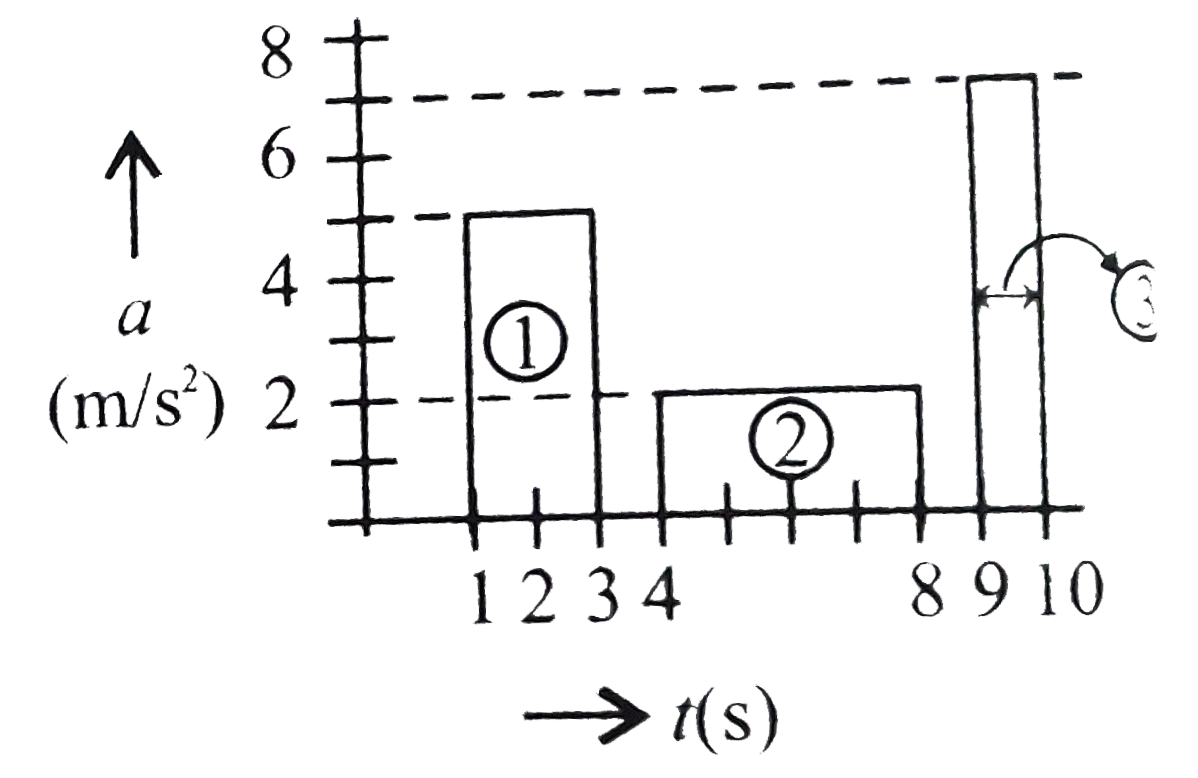
View SolutionThe figure shows a particle moving along x - axis subjected to three particles of acceleration (a). Rank the periods according to the increase they produce in the particle velocity, greatest first.
View Solution