The figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
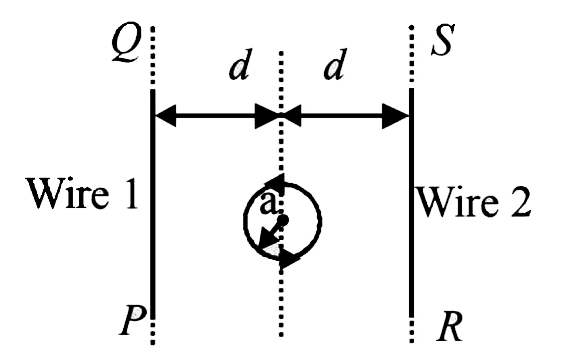
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that case
current in wire 1 and wire 2 is in the direction PQ and RS, respectively and h=a
current in wire 1 and wire 2 is in the direction PQ and SR, respectively and h=a
current in wire 1 and wire 2 is in the direction PQ and SR, respectively and h=1⋅2a
current in wire 1 and wire 2 is in the direction PQ and RS, respectively and h=1⋅2a
The correct Answer is:C
Let O be a point at a height h above the loop. The magnetic field induction at O due to current loop
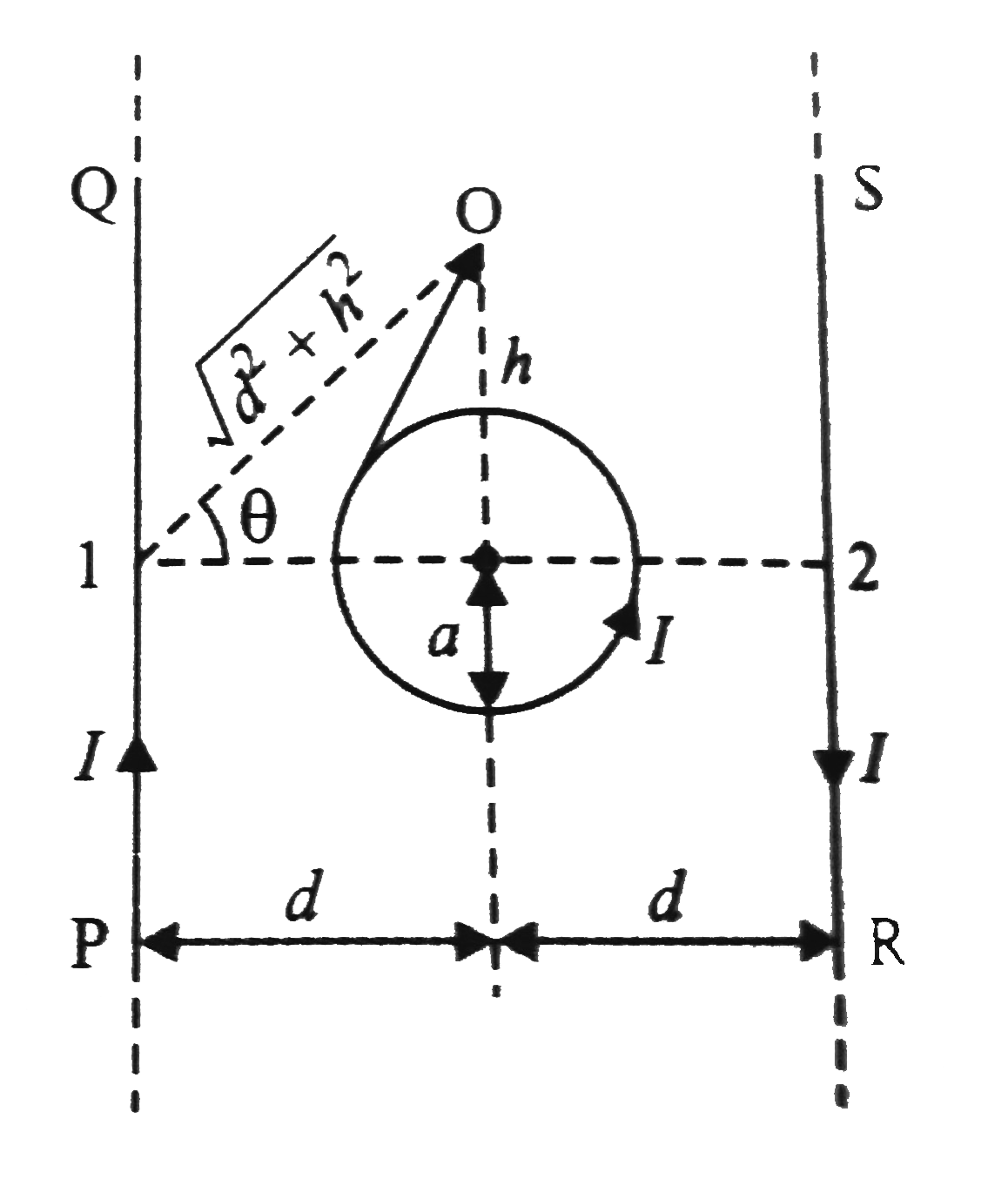
B1=μ04π2πIa2(a2+h2)3/2=μ0Ia22(a2+h2)3/2
Magnetic field induction at O due to currents in the wire 1 and 2.
B2=2×μ04π2I√d2+h2×d√d2+h2
=μ0Idπ(d2+h2)=μ0Iaπ(a2+h2)(∵d=a)
If net magnetic field at O is zero, then
B1=B2 or μ0Ia22(a2+h2)3/2=μ0Iaπ(a2+h2)
or a2√a2+h2=1π
or a24(a2+h2)=1π2=110 [∵π2=10]
or 10a2=4a2+4h2 or h2=3a2/2
or h=1⋅2a
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
A circular loop of radius 4.0 cm is placed in a horizontal plane and carries an electric current of 5.0 A in the clockwise direction as seen from above. Find the magnetic field (a) at a point 3.0 cm above the centre of the loop (b) at a point 3.0 cm below the centre of the loop.
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.

(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseAμ0I2a2dBμ0I2a22dC√3μ0I2a2dD√3μ0I2a22d - Question 2 - Select One
A circular loop of radius r carries a current i.How should a long, straight wire carrying a current 3i be placed in the plane of the circle so that the magnetic field at the centre of the loop becomes zero?
AAt at distances 3rπ from the centre of loopBAt at distances 2rπ from the centre of loopCAt at distances 2r3π from the centre of loopDNot possible - Question 3 - Select One
A non - planar loop of conducting wire carrying a current I is placed as shown in the figure . Each of the straighrt sections of the loop is of the length 2a. The magnetic field due to this loop at the point P(a,0,a) points in the direction
 A1√2(−ˆj+ˆk)B1√3(−ˆj+ˆk+ˆi)C1√3(ˆi+ˆj+ˆk)D1√2(ˆi+ˆk)
A1√2(−ˆj+ˆk)B1√3(−ˆj+ˆk+ˆi)C1√3(ˆi+ˆj+ˆk)D1√2(ˆi+ˆk)
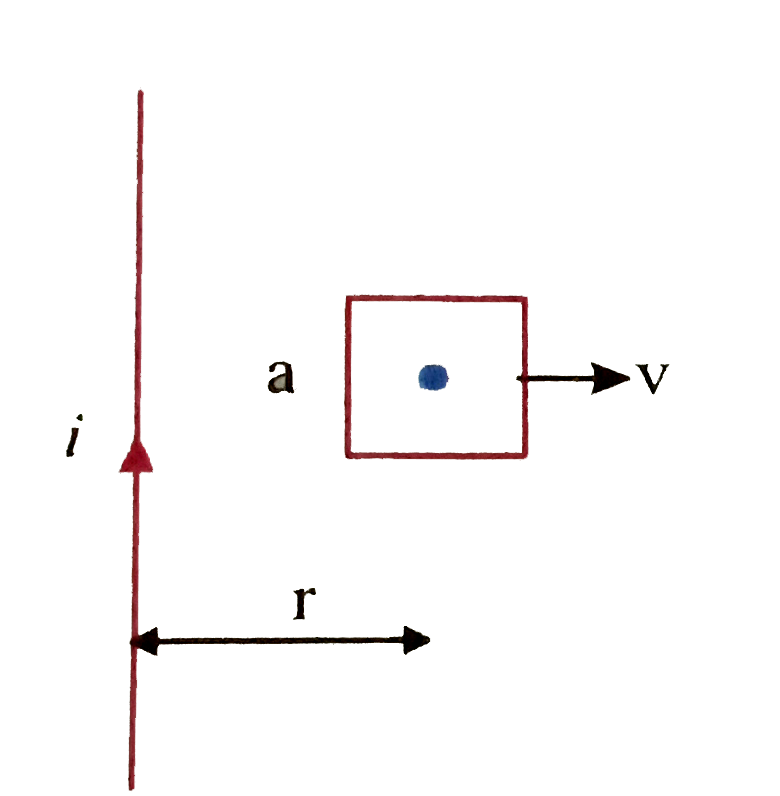
A square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
 View Solution
View SolutionA non-planar loop of conducting wire carrying a current 1 is placed as shown in the figure. Each of the straight sections of the loop is of length 2a. The magnetic field due to this loop at the point P (a,0, ) points in the direction
 View Solution
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View SolutionA steady current flows in a long wire. It is bent into a circular loop of one turn and the magnetic field at the center of the coil is B. If the same wire is bent into a circular loop of n turns, the magnetic field at the center of the coil is
View Solution

