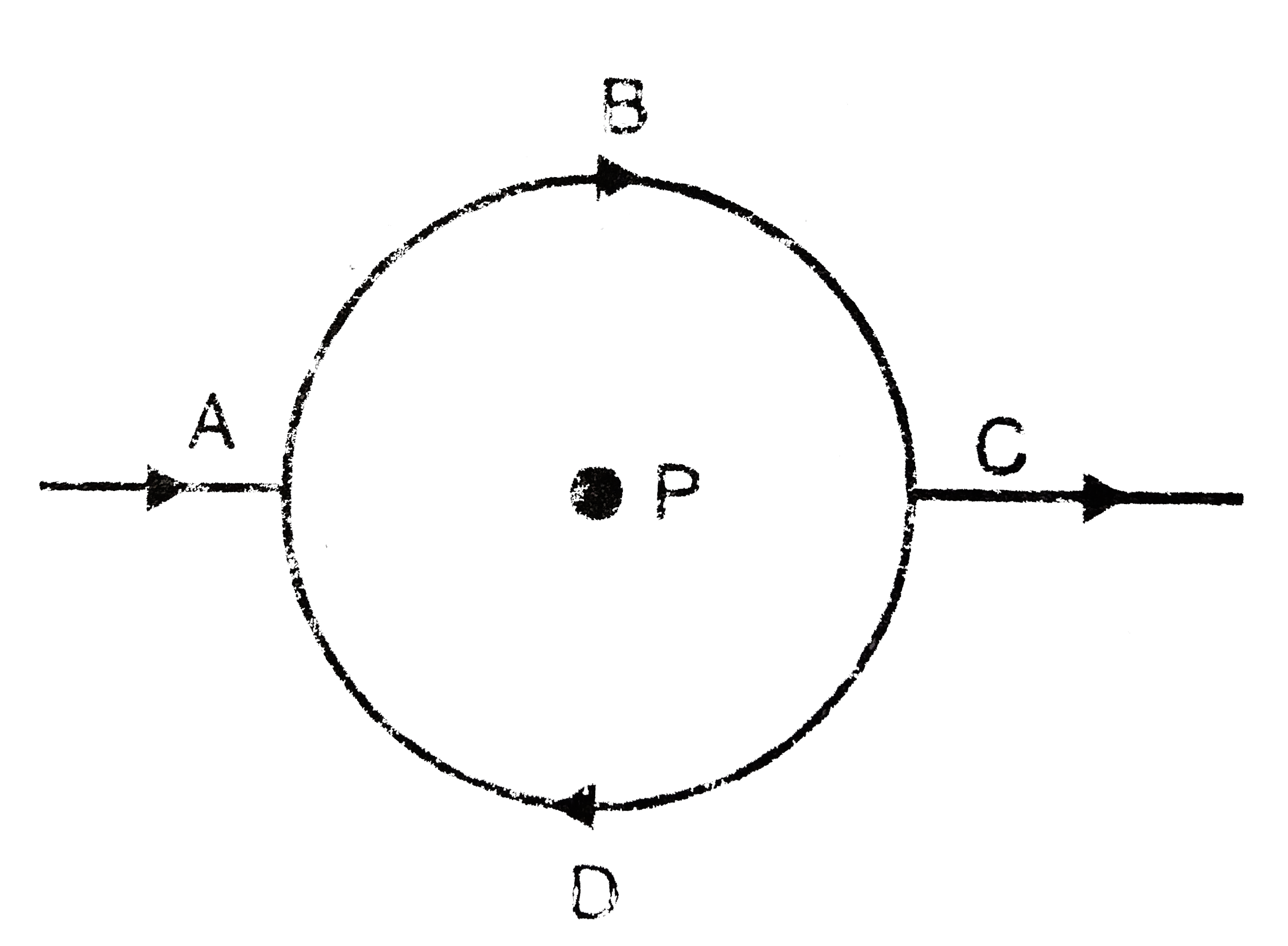
A conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

Magnetic field at P due to each straight wire is zero. B due ot ABC and ADC at P is equal in magnitude but opposite in direction. Hence net BatP=O.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
A wire loop formed by joining two semicircular wires of radii R1 and R2 carries a current I as shown in figure. Find the magnetic field induction at the centre O.

View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View Solution
Knowledge Check
The wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
 AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2)
AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2)A circular loop of radius r carries a current i.How should a long, straight wire carrying a current 3i be placed in the plane of the circle so that the magnetic field at the centre of the loop becomes zero?
AAt at distances 3rπ from the centre of loopBAt at distances 2rπ from the centre of loopCAt at distances 2r3π from the centre of loopDNot possibleA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
A circular loop of radius r carries a current i. How should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionA circular loop of radius R carries current I2 in a clockwise direction as shown in figure. The centre of the loop is a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the centre of loop is zero?
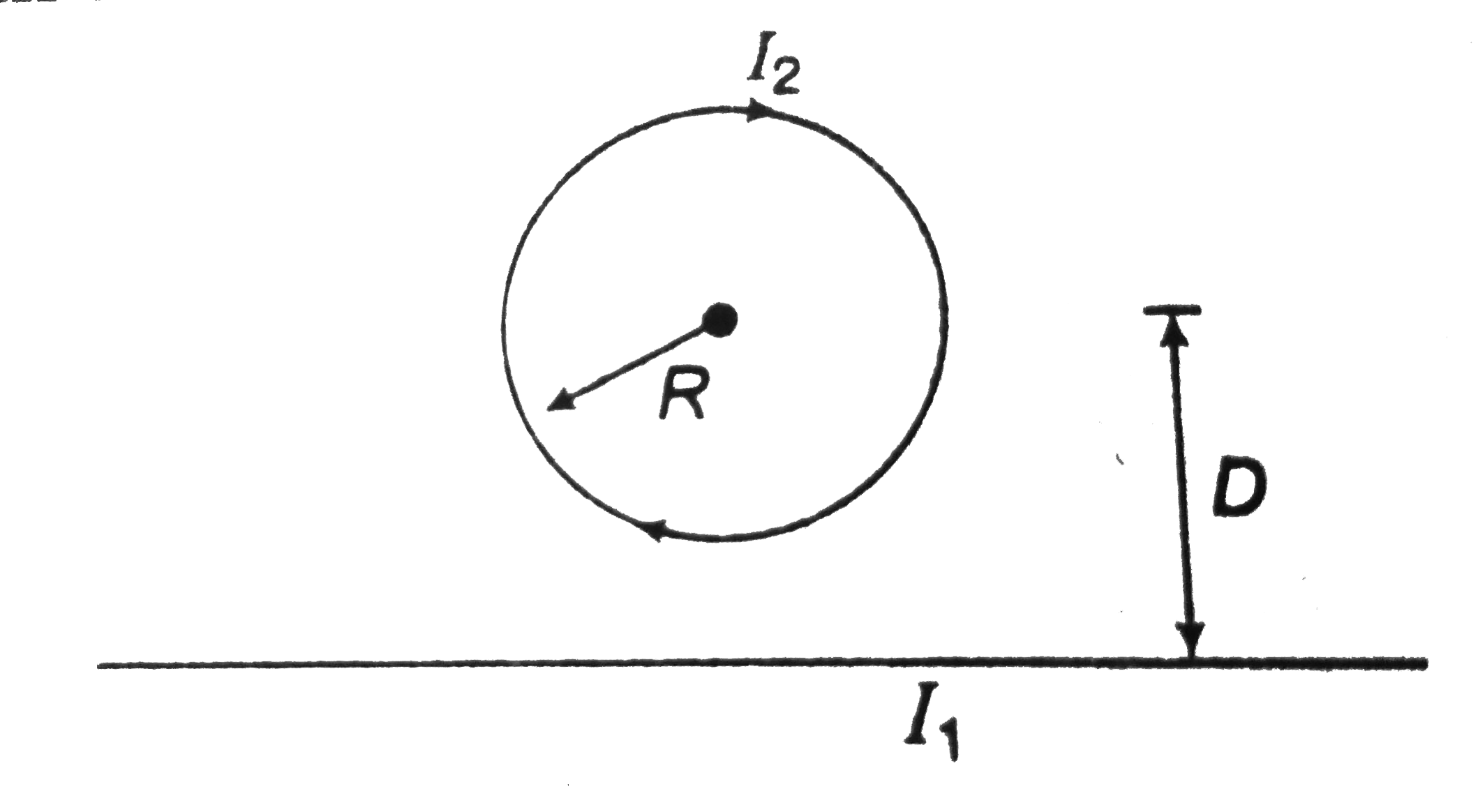
View SolutionA circular loop has radius R and carries current I2 in a clockwise direction (as shown in Fig.) The centre of the loop is at a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the center of the loop is zero?

View SolutionA rigid wire consists of a semicircular portion of radius R and two straight sections the wire is partially immersed in a perpendicular magnetic field B as shown in the figure. Find the magnetic force on the wire if it carries a current i.
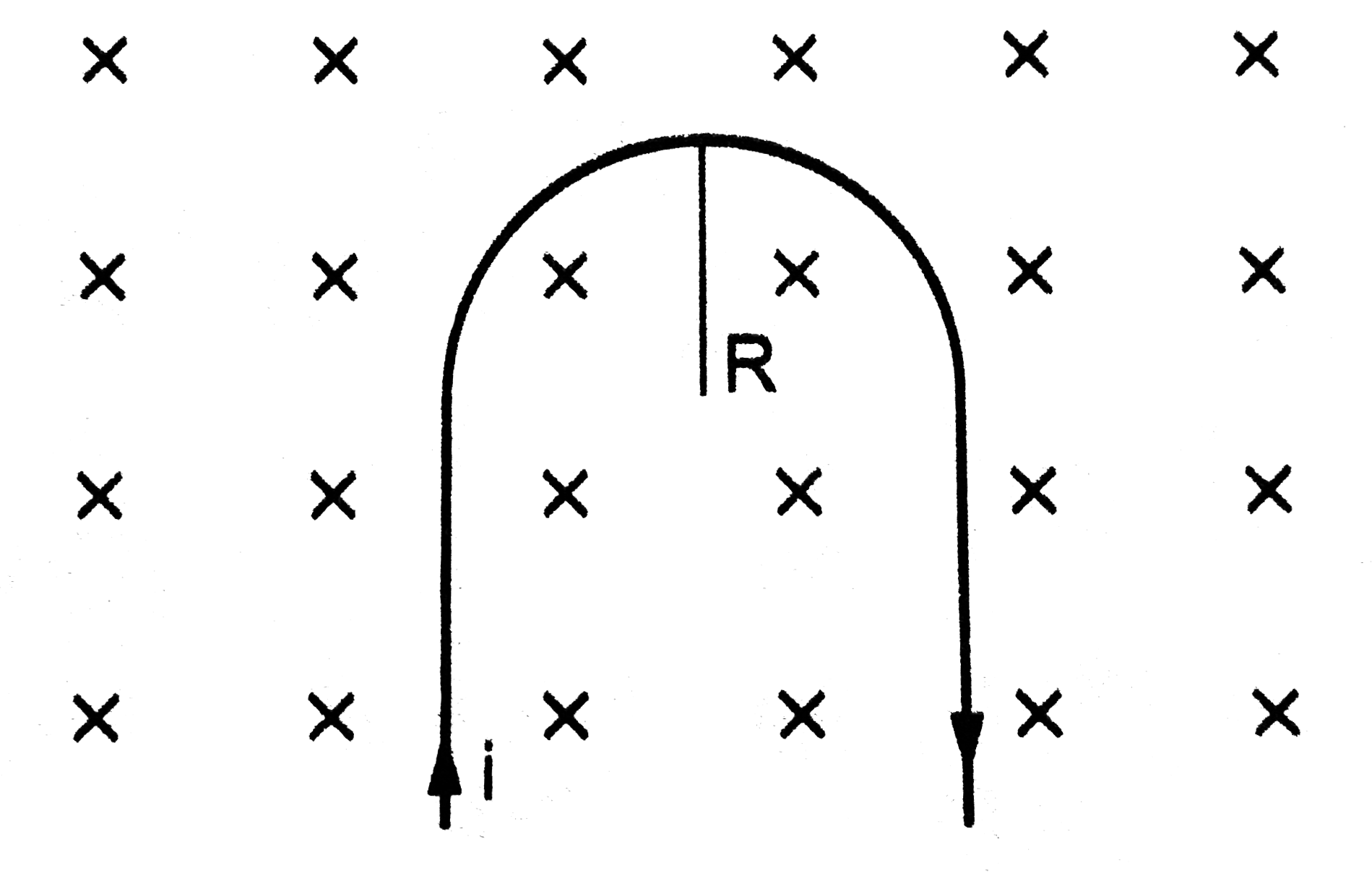
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View Solution
