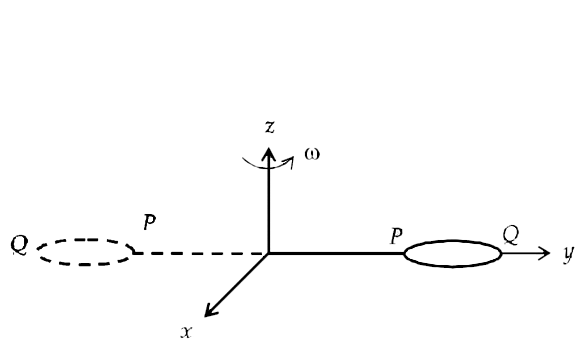
The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed $ω$ the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed $ω$ in this case

Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of $45^{\circ}$ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed $ω$ about the z-axis.

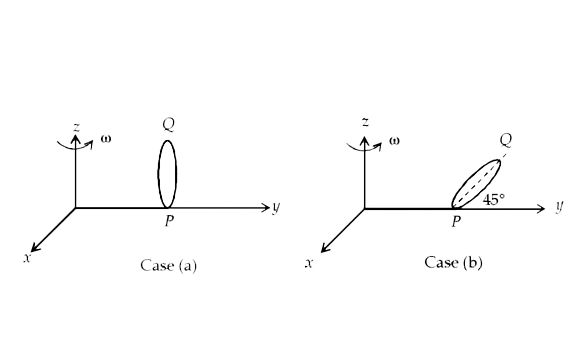
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?

It is $\sqrt{2} ω$ for both the cases

It is $ω$ for case a and $\frac{ω}{\sqrt{2}}$ for case b

It is $ω$ force case a and $\sqrt{2} ω$ for case b

It is $ω$ for both the case

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

The radius of gyration of an uniform rod of length $L$ about an axis passing through its centre of mass and perpendicular to its length is.
A $\frac{L}{\sqrt{2}}$
B $\frac{L^{2}}{\sqrt{12}}$
C $\frac{L}{\sqrt{3}}$
D $\frac{L}{\sqrt{2}}$
Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
AR
B $\frac{R}{2}$
C $\sqrt{2} R$
D $\frac{R}{\sqrt{2}}$
The mass of a body cannot be considered to be concentrated at the centre of mass of the body for the purpose of computing its moment of inertia.
For then the moment of inertia of every body about an axis passing through its centre of mass would be zero.
AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.
BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.
CStatement-1 is True, Statement-2 is False.
DStatement-1 is False, Statement-2 is True.