A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
First decrease and then increase
Remains constant
Decreases
Increases
To solve the problem regarding the angular momentum of a rotating disc with an insect moving from the center to the rim, we can follow these steps:
Step 1: Understand the System
We have a horizontal disc rotating about a vertical axis through its center. An insect of mass m is initially at the center of the disc and moves outward to the rim.
Hint: Identify the components of the system: the disc and the insect.
Step 2: Identify Angular Momentum
The angular momentum L of a system is given by the sum of the angular momentum of the disc and the angular momentum of the insect. The angular momentum of a rotating body is given by:
L=Iω
where I is the moment of inertia and ω is the angular velocity.
Hint: Recall the formula for angular momentum and how it applies to both the disc and the insect.
Step 3: Moment of Inertia of the Disc
The moment of inertia I of a disc about its center is given by:
Idisc=12MR2
where M is the mass of the disc and R is its radius.
Hint: Use the standard formula for the moment of inertia of a disc.
Step 4: Moment of Inertia of the Insect
When the insect is at the center, its contribution to the angular momentum is zero because its distance from the axis of rotation is zero. When the insect moves to the rim, its moment of inertia becomes:
Iinsect=mR2
Hint: Remember that the moment of inertia depends on the distance from the axis of rotation.
Step 5: Total Angular Momentum
Initially, when the insect is at the center:
Linitial=Idiscω+0=12MR2ω
When the insect moves to the rim:
Lfinal=Idiscω+Iinsectω=(12MR2+mR2)ω
Hint: Combine the contributions to angular momentum from both the disc and the insect.
Step 6: Conservation of Angular Momentum
Since there are no external torques acting on the system, the angular momentum of the system is conserved:
Linitial=Lfinal
This means:
12MR2ω=(12MR2+mR2)ω
Hint: Use the principle of conservation of angular momentum to relate the initial and final states.
Step 7: Conclusion
Since the angular momentum is conserved and does not change, we conclude that the angular momentum of the system remains constant as the insect moves from the center to the rim.
Final Answer: The angular momentum of the system remains constant.
We have a horizontal disc rotating about a vertical axis through its center. An insect of mass m is initially at the center of the disc and moves outward to the rim.
The angular momentum L of a system is given by the sum of the angular momentum of the disc and the angular momentum of the insect. The angular momentum of a rotating body is given by:
L=Iω
where I is the moment of inertia and ω is the angular velocity.
The moment of inertia I of a disc about its center is given by:
Idisc=12MR2
where M is the mass of the disc and R is its radius.
When the insect is at the center, its contribution to the angular momentum is zero because its distance from the axis of rotation is zero. When the insect moves to the rim, its moment of inertia becomes:
Iinsect=mR2
Initially, when the insect is at the center:
Linitial=Idiscω+0=12MR2ω
Lfinal=Idiscω+Iinsectω=(12MR2+mR2)ω
Since there are no external torques acting on the system, the angular momentum of the system is conserved:
Linitial=Lfinal
12MR2ω=(12MR2+mR2)ω
Since the angular momentum is conserved and does not change, we conclude that the angular momentum of the system remains constant as the insect moves from the center to the rim.
Topper's Solved these Questions
Similar Questions
A thin horizontal circular disc is roating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. During the journey of the insect, the angular speed of the disc.
View SolutionA ring of mass 10kg and diameter 0.4m is rotated about an axis passing through its centre. If it makes 1800 revolutions per minute then , the angular momentum of the ring is
View SolutionA horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -

View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

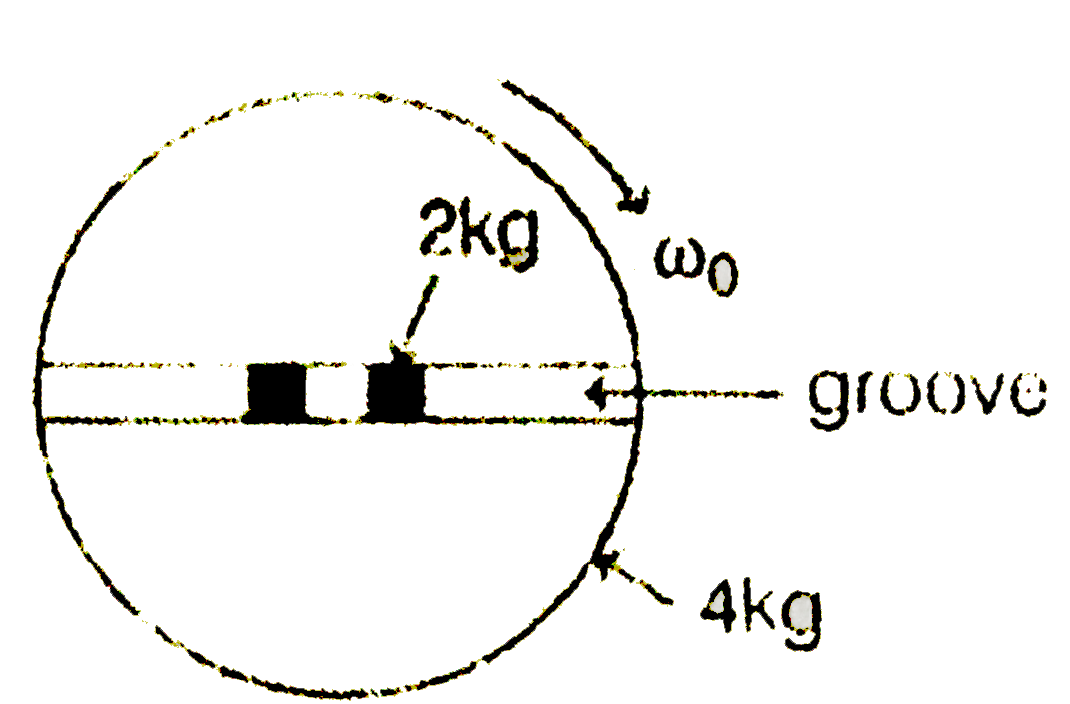
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity ω0 =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
View SolutionA cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
View Solution
