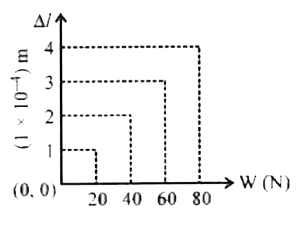
The given graph shows the extention (Δl) of a wire of length 1 m suspended from the top of a roof at one end with a load W connected to the other end. The cross-sectional area of the wire is 10−6m2. What is the Young's modulus of the material of the wire ?
3×10−12N/m2
2×10−13N/m2
2×1011N/m2
2×1010N/m2
The correct Answer is:C
From the graph of (Δl) against the laod (W), we find that for W=20N,Δl=10−4m,L=1m and A=10−6m2
∴Y=MgLA(Δ)=WLA(Δl)
=20×110−6×10−4=20×10+10=2×10+11N/m2
Topper's Solved these Questions
- ELASTICITYBOOK - MARVEL PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Test Your Grasp - 5
15 Videos
- CURRENT ELECTRICITYBOOK - MARVEL PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - MCQ
151 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS EXERCISE - TEST YOUR GRASP - 16
30 Videos
Similar Questions
The adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
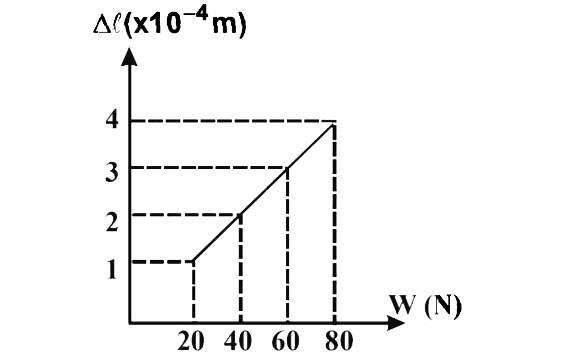
View SolutionThe adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .

View Solution
Knowledge Check
The adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
 A(a) 2×1011N/mB(b) 2×10−11N/mC(c) 3×10−12N/mD(d) 2×10−13N/m
A(a) 2×1011N/mB(b) 2×10−11N/mC(c) 3×10−12N/mD(d) 2×10−13N/mThe adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .
 A2×1011Nm−2B2×10−11Nm−2C3×10−12Nm2D2×10−13Nm2
A2×1011Nm−2B2×10−11Nm−2C3×10−12Nm2D2×10−13Nm2The adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .
 A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2
A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2
The adjacent graph shows the extra extension (Δx) of a wire of length 1m suspended from the top of a roof at one end with an extera load Δw connected to the other end If the cross sectional area of the wire is 10−5m2 calculate the Young's modulus of the meterial of the wire
(A) 2×1011N/m2 (B) 2×10−11N/m2 (c) 3×10913)N/m3 (D) 2×1016N/m2
 .
.
View SolutionThe adjacent graph shows the extra extension (Δx) of a wire of length 1m suspended from the top of a roof at one end with an extera load Δw connected to the other end If the cross sectional area of the wire is 10−5m2 calculate the Young's modulus of the meterial of the wire
(A) 2×1011N/m2 (B) 2×10−11N/m2 (c) 3×10913)N/m3 (D) 2×1016N/m2
 .
.
View Solution_S01_065_Q01.png)
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the young's modulus of the material of the wire is
(a). 2×1011Nm−2
(b). 2×1010Nm−2
(c). 12×1011Nm−2
(d). none of these
View Solution_S01_065_Q01.png)
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the young's modulus of the material of the wire is
(a). 2×1011Nm−2
(b). 2×1010Nm−2
(c). 12×1011Nm−2
(d). none of these
View SolutionThe graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the Young's modulus of the material of the wire.

View Solution
