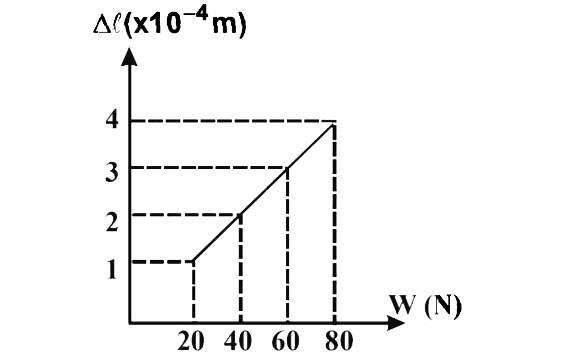
The adjacent graph shows the extra extension $(Δ x)$ of a wire of length $1 m$ suspended from the top of a roof at one end with an extera load $Δ w$ connected to the other end If the cross sectional area of the wire is $10^{- 5} m^{2}$ calculate the Young's modulus of the meterial of the wire
(A) $2 \times 10^{11} N / m^{2}$ (B) $2 \times 10^{- 11} N / m^{2}$ (c) $3 \times 10^{913}) N / m^{3}$ (D) $2 \times 10^{16} N / m^{2}$
.

Text Solution

Verified by Experts

$Δ l = (\frac{l_{0}}{A Y}) Δ w s l o p e = \frac{l_{0}}{A Y} = \frac{1 \times 10^{- 4}}{20} \Rightarrow \frac{1}{(10^{- 6}) Y} = \frac{1 \times 10^{- 4}}{20}$
$Y = 20 \times 10^{10} = 2 \times 10^{11} N / m^{2}$ .

Updated on:21/07/2023

|

Class 12 PHYSICS EXPERIMENTAL PHYSICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The adjacent graph shows the extension $Δ l$ of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is $10^{6} m^{2}$ calculate the young's modulus of the material of the wire .

A $2 \times 10^{11} N m^{- 2}$
B $2 \times 10^{- 11} N m^{- 2}$
C $3 \times 10^{- 12} N m^{2}$
D $2 \times 10^{- 13} N m^{2}$
The adjacent graph shows the extension $Δ l$ of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is $10^{6} m^{2}$ calculate the young's modulus of the material of the wire .

A $2 \times 10^{11} N / m^{2}$
B $2 \times 10^{- 11} N / m^{2}$
C $3 \times 10^{- 12} N / m^{2}$
D $2 x 10^{- 13} N / m^{2}$
The adjacent graph shows the estension $(Δ l)$ of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is $10^{- 6} m^{2}$ , calculate the Young's modulus of the material of the wire.

A(a) $2 \times 10^{11} N / m$
B(b) $2 \times 10^{- 11} N / m$
C(c) $3 \times 10^{- 12} N / m$
D(d) $2 \times 10^{- 13} N / m$

RESONANCE-EXPERIMENTAL PHYSICS-PART -II

Home
Ask Doubt
Profile