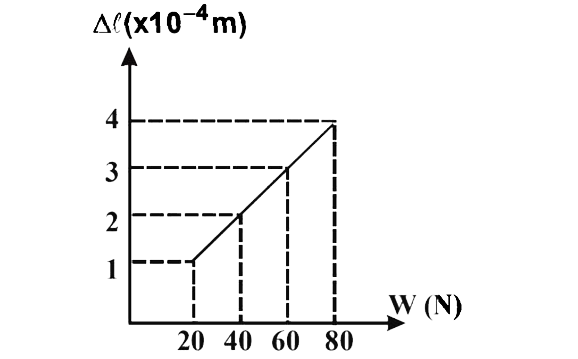
The graph as in Fig. shows the extension ( $Δ L$ ) of a wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. Area of cross-section of the wire is $10^{- 6} m^{2}$ . Find Y in SI units:

A

$2 \times 10^{6} N / m^{2}$

B

$2 \times 10^{11} N / m^{2}$

C

$5 \times 10^{6} N / m^{2}$

D

$5 \times 10^{11} N / m^{2}$

Text Solution

Verified by Experts

The correct Answer is:B

Young.s modulus Y= $\frac{F}{A} \times \frac{l}{Δ l}$
$= \frac{20 \times 1}{10^{- 6} \times 10^{- 4}} = 2 \times 10^{11} N / m^{2}$
So correct choice is (b).

Updated on:21/07/2023

|

Class 12 PHYSICS PROPERTIES OF MATTER

Topper's Solved these Questions

Similar Questions

Knowledge Check

The adjacent graph shows the extension $Δ l$ of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is $10^{6} m^{2}$ calculate the young's modulus of the material of the wire .

A $2 \times 10^{11} N m^{- 2}$
B $2 \times 10^{- 11} N m^{- 2}$
C $3 \times 10^{- 12} N m^{2}$
D $2 \times 10^{- 13} N m^{2}$
The adjacent graph shows the extension $Δ l$ of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is $10^{6} m^{2}$ calculate the young's modulus of the material of the wire .

A $2 \times 10^{11} N / m^{2}$
B $2 \times 10^{- 11} N / m^{2}$
C $3 \times 10^{- 12} N / m^{2}$
D $2 x 10^{- 13} N / m^{2}$
The adjacent graph shows the estension $(Δ l)$ of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is $10^{- 6} m^{2}$ , calculate the Young's modulus of the material of the wire.

A(a) $2 \times 10^{11} N / m$
B(b) $2 \times 10^{- 11} N / m$
C(c) $3 \times 10^{- 12} N / m$
D(d) $2 \times 10^{- 13} N / m$

MODERN PUBLICATION-PROPERTIES OF MATTER-RECENT COMPETITIVE QUESTIONS

Home
Ask Doubt
Profile