The graph between period of oscillation (T) and mass attached (m) to a spring will be
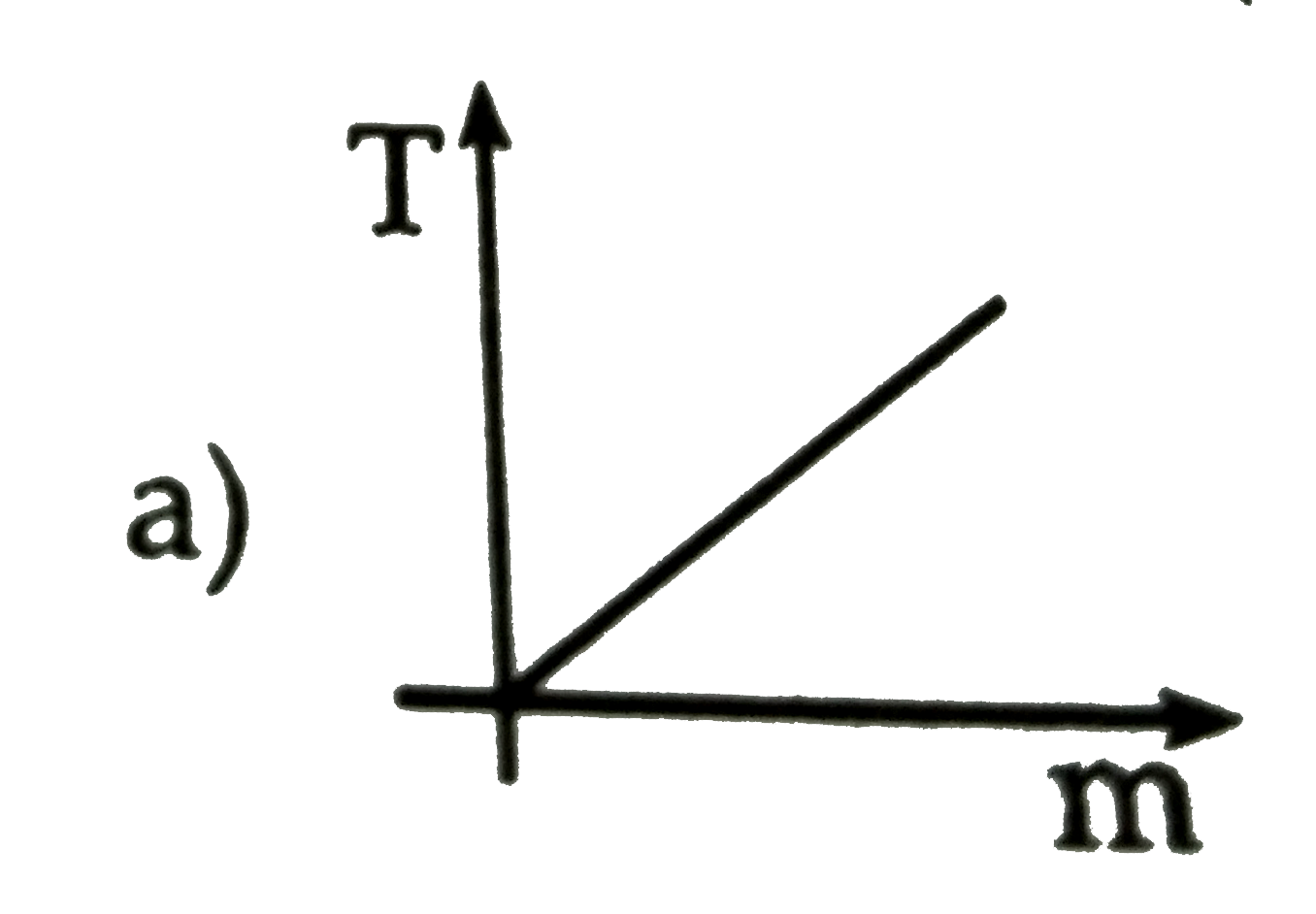

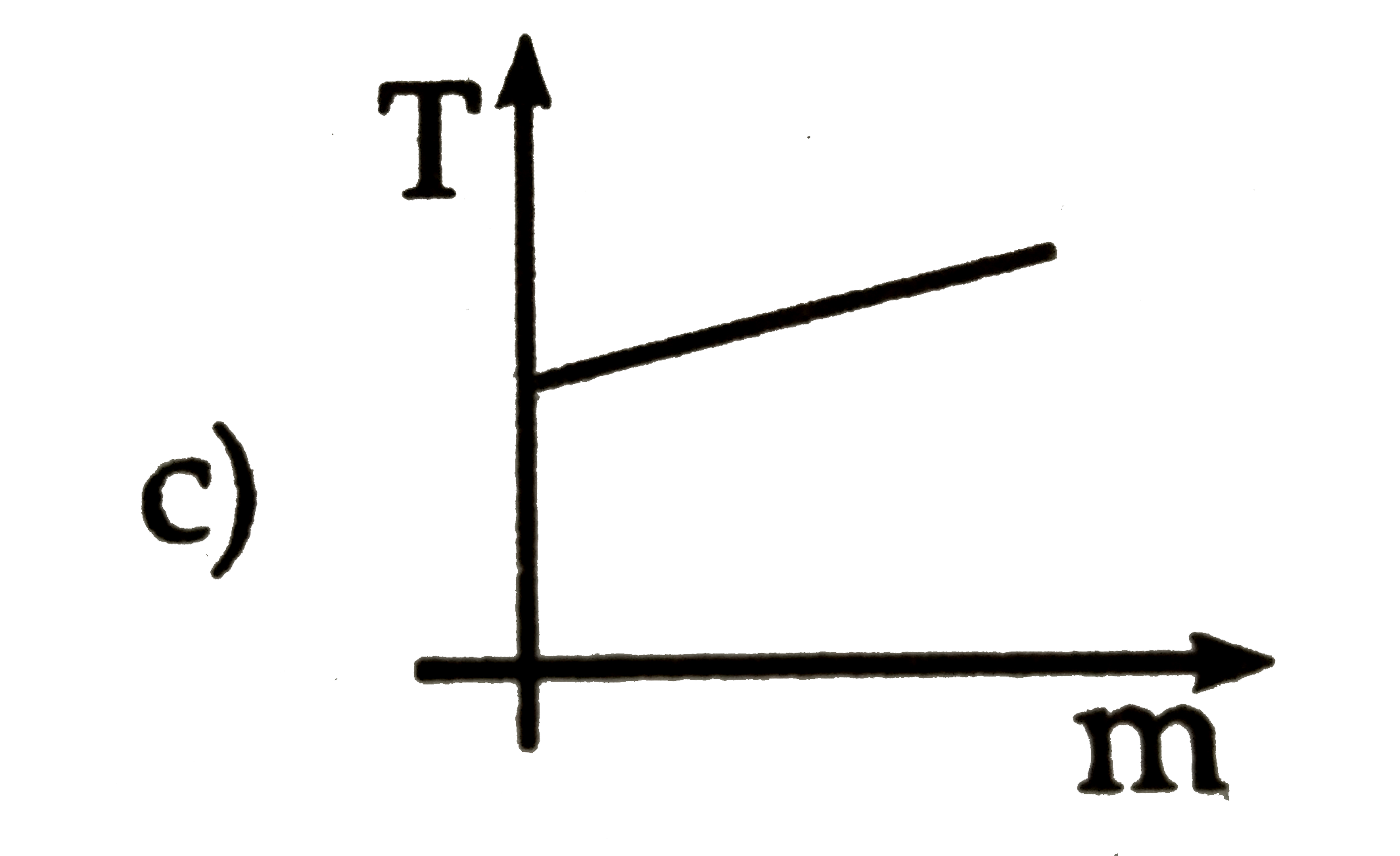
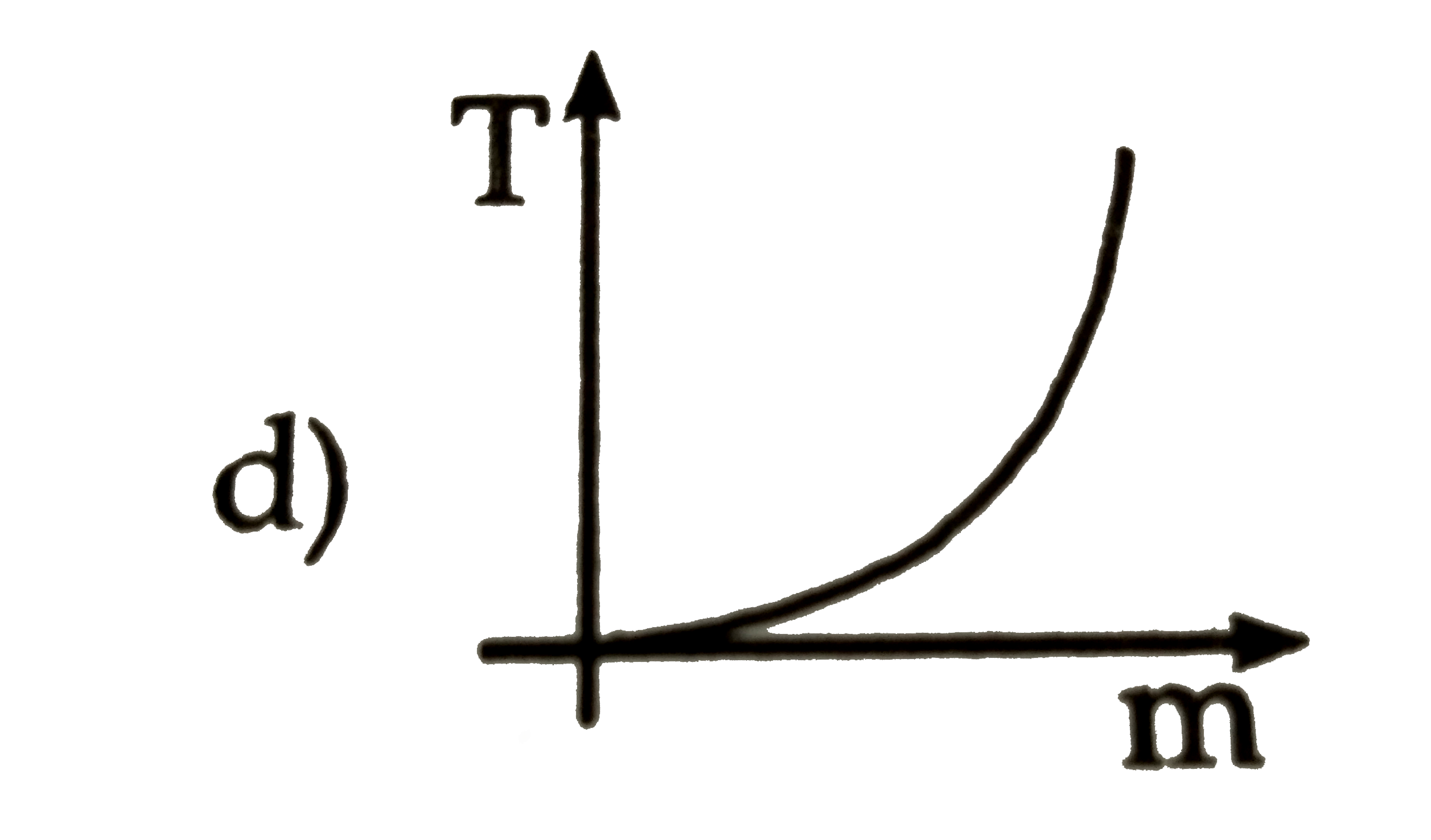
Step by step video, text & image solution for The graph between period of oscillation (T) and mass attached (m) to a spring will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionA 2kg mass is attached to a spring of force constant 600N/m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m/s.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t=0. What is the impulse given to the 2kg mass in each case ?
View Solution
Knowledge Check
The time period of oscillations of a block attached to a spring is t1. When the spring is replaced by another spring, the time period of the block is t2. If both the springs are connected in series and the block is made to oscillate using the combination, then the time period of the block is
AT=t1+t2BT2=t21+t22CT−1=t−11+t−12DT−2=t−21+t−22If a graph is plotted for the square of period (T2) and mass attached to a spring, its shape will be
A B
B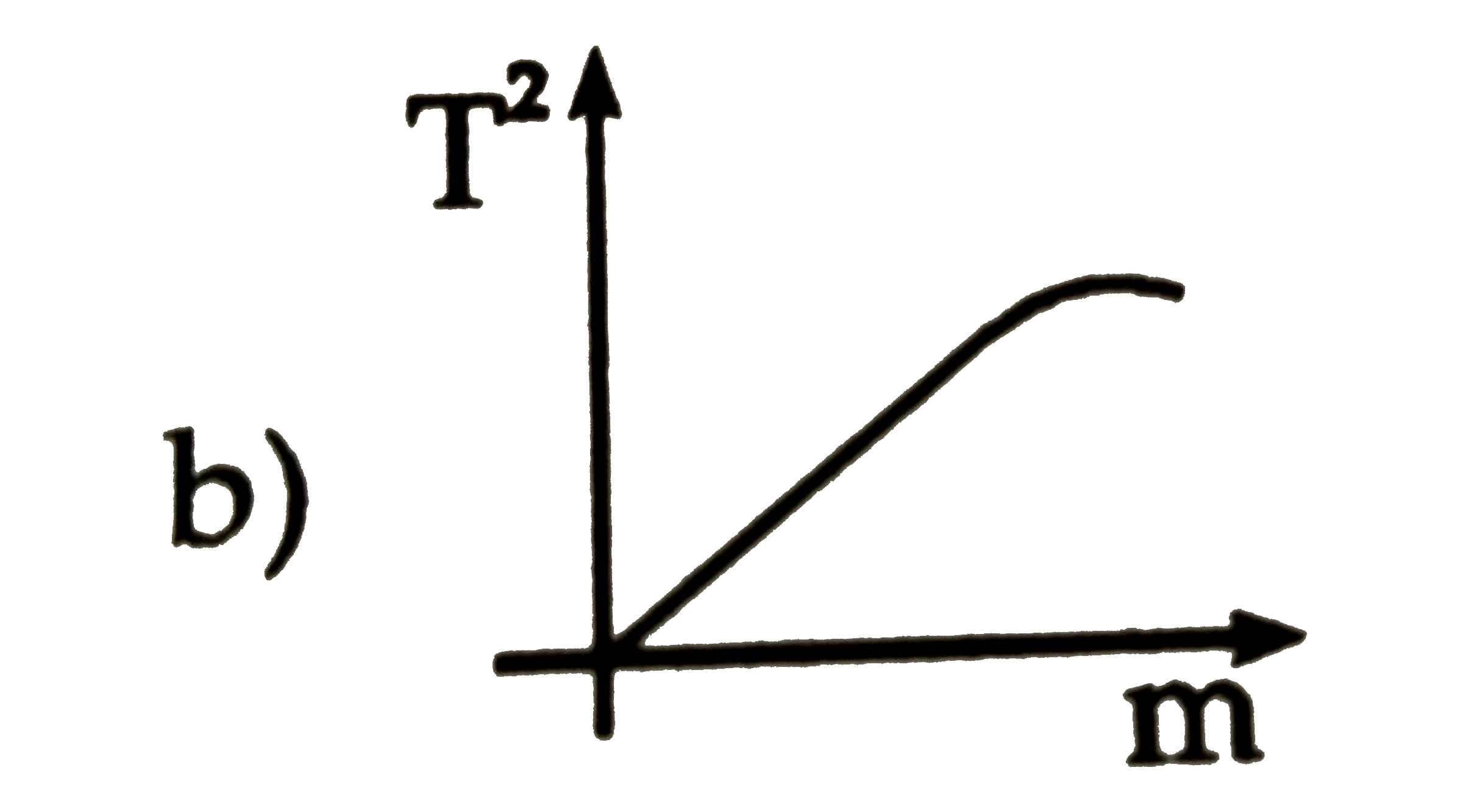 C
C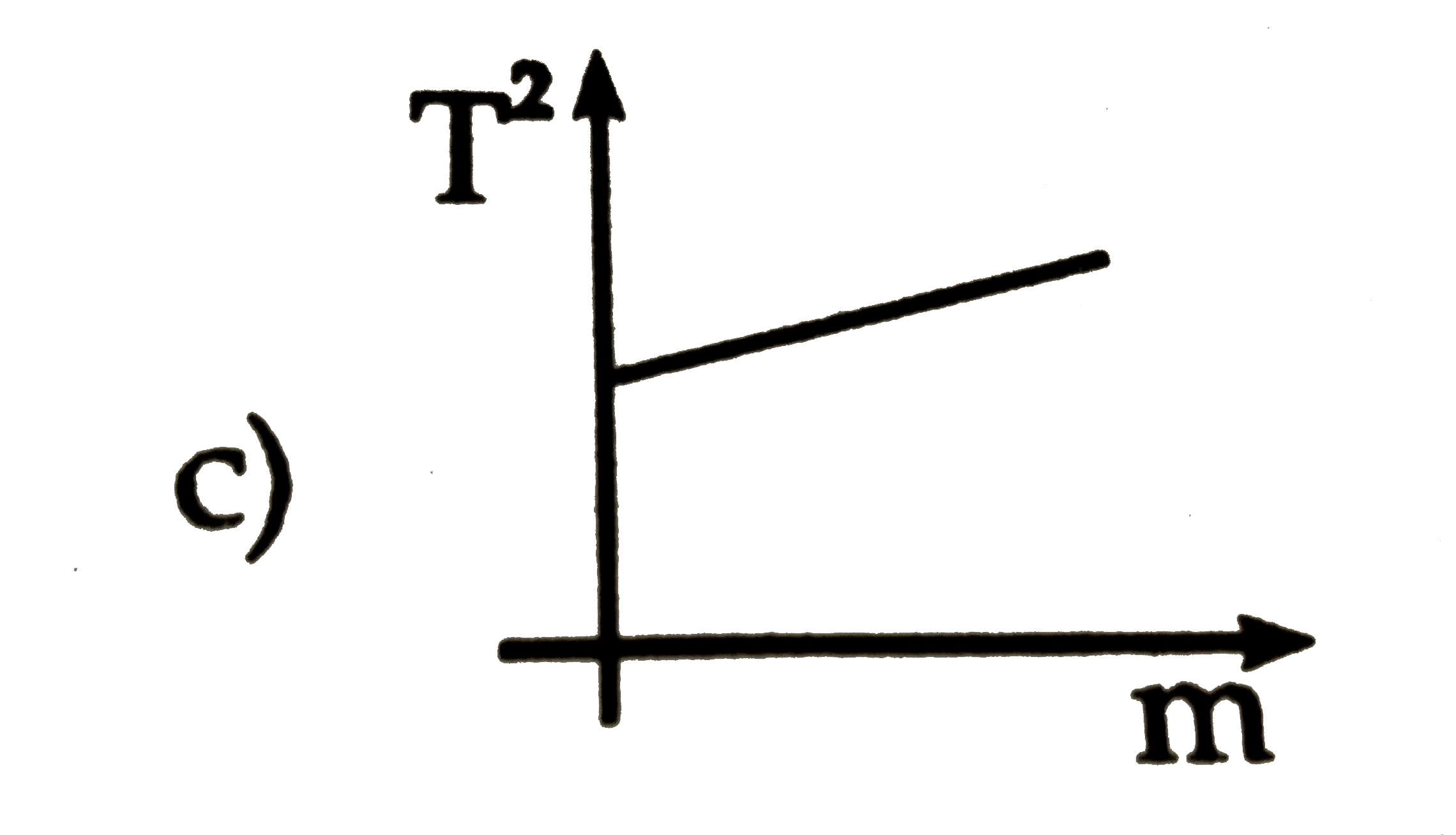 D
D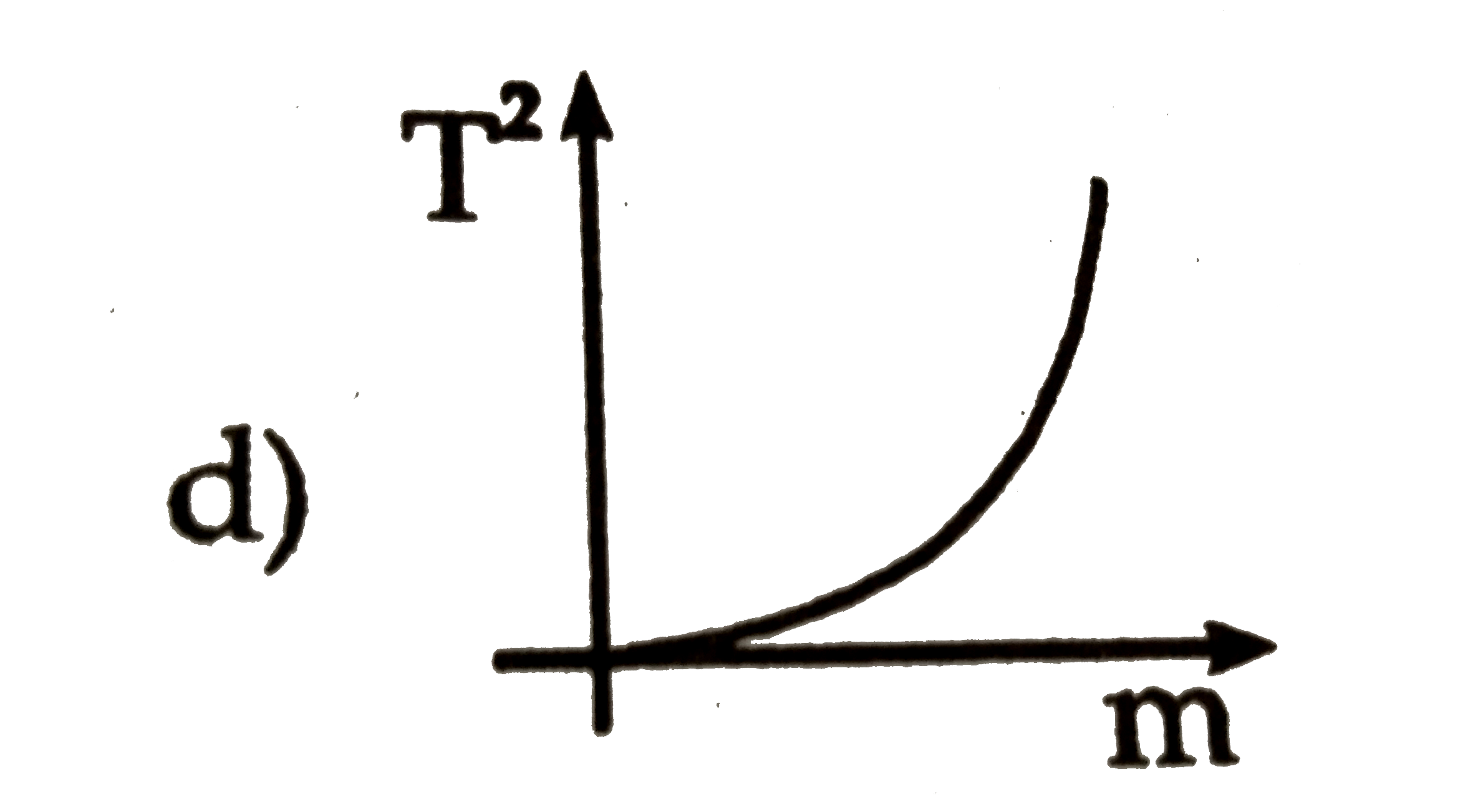
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
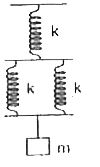 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
The graph shown was obtained from experimental measurements of the period of oscillations T for different masses M placed in the scale pan on the lower end of the spring balance. The most likely reason for the line not passing through the origin is that the
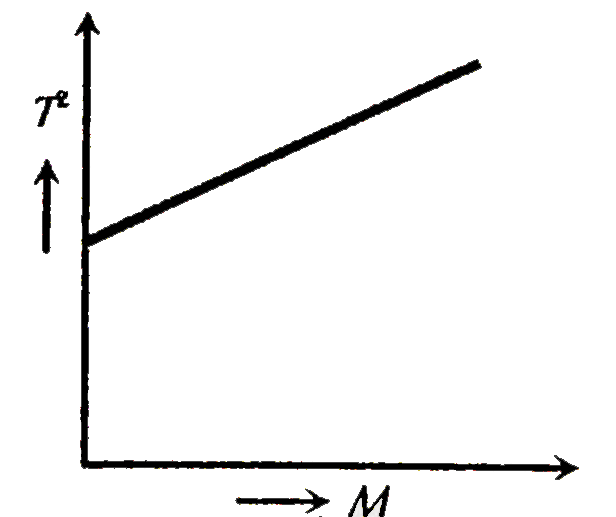
View SolutionThe period of oscillation of a mass M, hanging from a spring of force constant k is T. When additional mass m is attached to the spring, the period of oscillation becomes 5T/4. m/M =
View SolutionThe period of oscillation of mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be
View SolutionIf the period of oscillation of mass m suspended from a spring is 2 s, then the period of mass 4 m will be
View SolutionA vertical spring has a time period of oscillations of T1 with a load m1 at its end. Its time period is T2 when the load is replaced by another of mass m2. The force constant of the spring is
View Solution
