The gravitational field in a region is given by $E = (2 \to i + \to j) N k g^{- 1}$ show that no work is done by the gravitational field when particle is move on the line $3 y + 2 x = 5$ .

Video Solution

Text Solution

Verified by Experts

$3 y + 2 x = 5 \Rightarrow y = - \frac{2}{3} x + \frac{5}{3}$
$tan θ = - (2 / 3)$

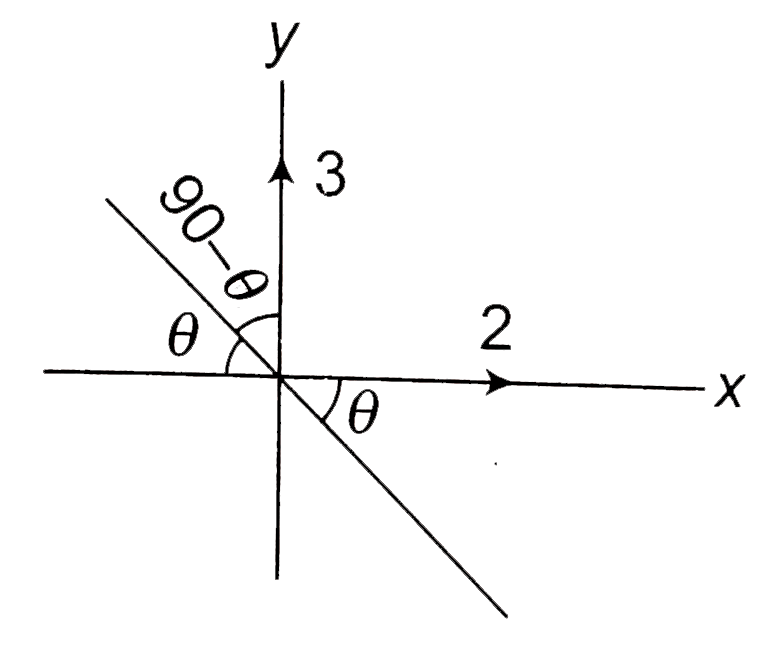
Gravitational field along the straight line $3 y + 2 x = 5$
$E' = 2 cos (90 - θ) - 2 cos θ$
$= 3 sin θ - 2 cos θ$
$= 3 \times \frac{2}{\sqrt{13}} - 2 \times \frac{3}{\sqrt{13}} = 0$
$W = m E' = 0$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The gravitational field in a in region is given by $\to g = (4 ˆ i + \to j) N / k g$ . What done by this field is zero when the particle is moved along the line :
A $y + 4 x = 2$
B $4 y + x = 6$
C $x + y = 5$
Dall of the above
Question 2 - Select One
The gravitational field in a region is given by $\to g = (5 ˆ i + 12 ˆ j) {N kg}^{- 1}$ . The change in the gravitational potential energy of a particle of mass 2kg when it is taken from the origin to a point $(7 m, - 3 m)$ is
A71 J
B $13 \sqrt{58} J$
C2 J
D1 J
Question 3 - Select One
The gravitational field in a region is given by $\to E = (y ˆ i + x ˆ j)$ N/kg, where x and y are in metres. The equipotential lines are plotted as
A
B
C
D

CP SINGH-GRAVITATION-EXERCISE

Home
Ask Doubt
Profile