The gravitational force between a H-atom and another particle of mass m will be given by Newton's law
F=GM.mr2, where r is in km and
For mp=10−6 times, the mass of an electron , the energy associated with it is given by
mpc2=10−6×electron mass×c2
=10−6×0.5MeV
=10−6×0.5×1.6×10−19
=0.8×10−13J
The wavelength associated with is given by
hmpc=hcmpc2=10−34×3×1080.8×10−19
≈4×10−7m>> Bohr radius
|F|=e24πε0[1r2+λr]exp(−λr)
where λ−1=hmpc≈4×10−7m>>rB
∴λ<<1rB i.e., λrB<<1
U(r)=−e4πε0.exp(−λr)r
mvr=h∴v=hmr
Also, mv2r=≈(e24πε0)[1r2+λr]
∴h2mr3=(e24πε0)[1r2+λr]
∴h2m=(e24πε0)[r+πr2]
If λ=0,r=rB=hm.4πε0e2
h2m=e24πε0.rB
Since, λ−1>>rB, put r=rB+δ
∴rB=rB+δ+λ(r2B+δ2+2δrB), neglect δ2
or 0=λr2B+δ(1+2λrB)
δ=−λr2B1+2λrB≈λr2B(1+2λrB)=−λr2B
Since, λrB<<1
∴V(r)=−e24πε0.exp(−λδ−λrB)rB+δ
∴V(r)=−e24πε01rB[(1−δrB).(1−λrB)]
≅(−27.2eV) remains unchanged
KE=−13mv2=12m.h2mr2=h22(rB+δ)2=h22r2B(1−2δrB)
=(13.6eV)[1+2λrB]
Total energy =−e24πε0rB+h22r2B[1+2λrB]
=−27.2+13.6[1+2λrB]eV
Change in energy =13.6×2λrBeV=27.2λrBeV
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ATOMSEXERCISE - Short Answer Type5videos
ATOMS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Long Answe types Questions5videos
ALTERNATING CURRENT
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - LONG ANSWER TYPE QUESTIONS5videos
COMMUNICATION SYSTEM
Similar Questions
Assertion : Mass of the rod AB is m1 and of particle P is m2. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
F=Gm1m2r2
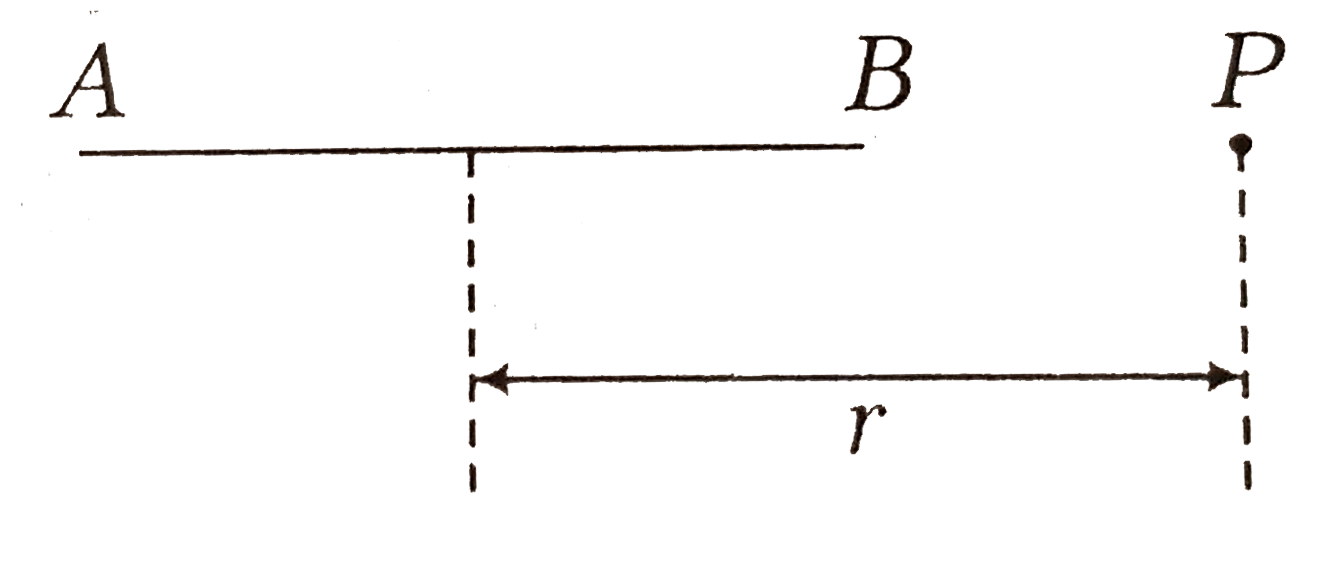
Reason : The relation F=Gm1m2r2 can be applied directly only to find force between two particles.View SolutionThe gravitational force between two objects is proportional to 1/R (and not as 1/R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
View Solution
Knowledge Check
- Question 1 - Select One
The gravitational force F between two masses m1andm2 separeted by a distance r is given by
F=Gm1m2r2
Where G is the universal gravitational constant. What are the dimensions of G ?AM−1L2T−3BM−1L3T−2CML3T−2DML2T−3 - Question 2 - Select One
Two sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
A3FBFCF3DF9
The gravitational force between two objects is proportional to 1/R (and not as 1/R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
View SolutionIf gravitational attraction between two points masses be given by F=Gm1m2rn. Then the period of a satellite in a circular orbit will be proportional to
View SolutionTwo sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
View SolutionTwo sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
View SolutionStatement I: The force of gravitation between a sphere and a rod of mass M2 is =(GM1M2)/r.
Statement II: Newton's law of gravitation holds correct for point masses.
 View Solution
View SolutionAssertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.View Solution

