The half life of a radioactive element is T and its initial activity at t=0 is A0 and at t=t it is A, then
A=A02t/T
A=A0(2t)T
A0=A2t/T
A0=A2−t/T
The correct Answer is:C
Step by step video, text & image solution for The half life of a radioactive element is T and its initial activity at t=0 is A_(0) and at t=t it is A, then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A radioactive element decays to 1/32th of its initial activity in 25 decay. Calculate its half life.
View SolutionHalf-life of a radioactive substance is T. At time t_1 activity of a radioactive substance is R1 and at time t2 it is R2. Find the number of nuclei decayed in this interval of time.
View Solution
Knowledge Check
- Question 1 - Select One
The t0.5 of a radioactive element is related to its average life by the expression
AT12=1.44TavBT12=1.36TavCT12=0.693TavDT12=Tav0.693 - Question 2 - Select One
The half-life of a radioactive sample is T. If the activities of the sample at time t1 and t2 (t1<t2) and R1 and R2 respectively, then the number of atoms disintergrated in time t2−t1 is proportional to
A(R1−R2)TB(R1+R2)TCR1R2R1+R2TDR1R2T - Question 3 - Select One
The relation between half-life T of a radioactive sample and its mean life τis:
AT=0.693τBτ=0.693TCτ=TDτ=2.718T
To determine the half life of a radioactive element , a student plot a graph of in ∣∣∣dN(t)dt∣∣∣ versus t , Here ∣∣∣dN(t)dt∣∣∣ is the rate of radiation decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after 4.16year the value of p is
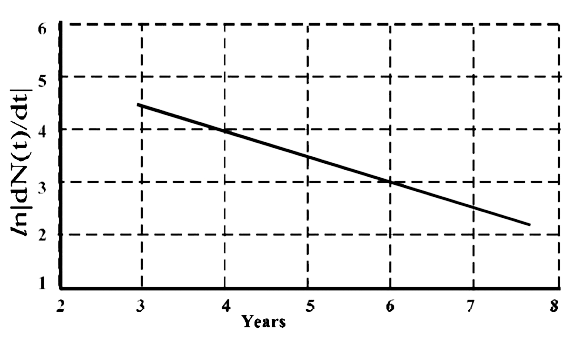 View Solution
View SolutionThe activity of a radioactive element decreases in 10 years to 1/5 of initial activity A0. After further next 10 years, its activity will be
View SolutionThe t0.5 of a radioactive element is related to its average life by the expression
View SolutionThe half life of radioactive substance is T. Then the fraction of the substance that has decayed in time t is-
View SolutionThe half life of a radioactive substance is T0. At t=0,the number of active nuclei are N0. Select the correct alternative.
View Solution

