The height of a mercury barometer is 75 cm at sea level and 50 cm at the top of a hill. Ration of density of mercury to that of air is 104. The height of the hill is
250 m
2.5 km
1.25 km
750 m
The correct Answer is:B
To solve the problem of finding the height of the hill based on the given data about the mercury barometer, we can follow these steps:
Step 1: Understand the Problem
We have two heights of mercury in a barometer:
- At sea level (H1) = 75 cm
- At the top of the hill (H2) = 50 cm
We also know the ratio of the density of mercury (ρ_M) to the density of air (ρ_air) is 10^4.
Step 2: Write the Pressure Equations
The pressure at sea level (P1) can be expressed as:
P1=ρMgH1
The pressure at the top of the hill (P2) can be expressed as:
P2=ρMgH2
Step 3: Calculate the Change in Pressure
The change in pressure (ΔP) between the two locations is:
ΔP=P1−P2=ρMg(H1−H2)
Step 4: Relate Change in Pressure to Height of the Hill
The change in pressure due to the height of the hill (h) can be expressed as:
ΔP=ρairgh
Step 5: Equate the Two Pressure Changes
Setting the two expressions for ΔP equal gives us:
ρMg(H1−H2)=ρairgh
We can cancel g from both sides:
ρM(H1−H2)=ρairh
Step 6: Substitute the Density Ratio
Using the given ratio of densities:
ρMρair=104
We can rewrite the equation as:
104(H1−H2)=h
Step 7: Calculate the Height of the Hill
Substituting the values of H1 and H2:
h=104(75cm−50cm)
h=104(25cm)
h=250000cm
Step 8: Convert to Kilometers
To convert centimeters to kilometers:
h=250000cm100000=2.5km
Final Answer
The height of the hill is 2.5 kilometers.
---
We have two heights of mercury in a barometer:
- At sea level (H1) = 75 cm
- At the top of the hill (H2) = 50 cm
The pressure at sea level (P1) can be expressed as:
P1=ρMgH1
The pressure at the top of the hill (P2) can be expressed as:
P2=ρMgH2
The change in pressure (ΔP) between the two locations is:
ΔP=P1−P2=ρMg(H1−H2)
The change in pressure due to the height of the hill (h) can be expressed as:
ΔP=ρairgh
Setting the two expressions for ΔP equal gives us:
ρMg(H1−H2)=ρairgh
We can cancel g from both sides:
ρM(H1−H2)=ρairh
Using the given ratio of densities:
ρMρair=104
We can rewrite the equation as:
104(H1−H2)=h
Substituting the values of H1 and H2:
h=104(75cm−50cm)
h=104(25cm)
h=250000cm
To convert centimeters to kilometers:
h=250000cm100000=2.5km
The height of the hill is 2.5 kilometers.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
The vertical height of mercury which a simple barometer can support at sea level is:
View SolutionThe vertical height of mercury in a simple barometer is dependant on the area of cross-section of barometer tube.
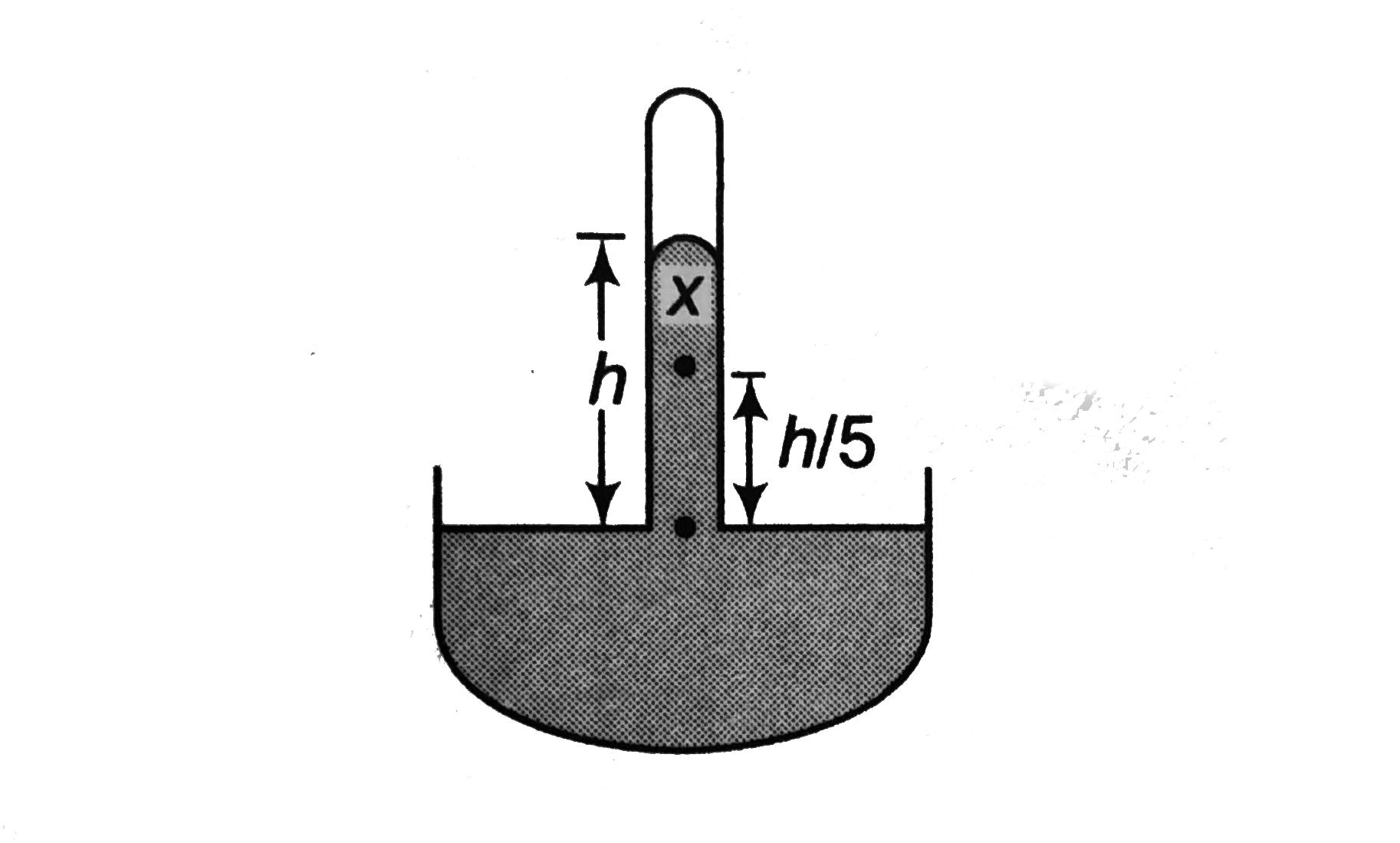
View SolutionThe height of mercury barometer is h when the atmospheic pressure is 105Pa. The pressure at x in the shown diagram is
View Solution(a) Calculate the height of a water column which will exert on its base the same pressure as the 70 cm column of mercury. Density of mercury is 13.6gcm−3
(b) Will the height of the water column in part (a) change if the cross section of the water column is made wider ?
View SolutionThe column of mercury in a barometer is 76mm of Hg. Calculate the atmospheric pressure if the density of mercury = 13600kgm −3 . (Take g=10ms −2 )
View SolutionThe top of a hill observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. The height of the hill is
View SolutionThe top of a hill observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. The height of the hill is
View SolutionA barometer correctly reads the atmospheric pressure as 76cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then become constant. If the saturation vapour pressure at the atmospheric temperature is 0.80cm of mercury, find the height if the mercury column when it reaches its minimum value.
View SolutionA man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60∘ and the angle of depression the base of hill as 30∘. Find the distance of the hill from the ship and the height of the hill.
View SolutionThe angle of elevation of the top of a hill at the foot of a tower is 60∘ and the angle of elevation of the top of the tower from the foot of the hill is 30∘ . If the tower is 50 m high, what is the height of the hill?
View Solution
