(a) Calculate the height of a water column which will exert on its base the same pressure as the 70 cm column of mercury. Density of mercury is 13.6gcm−3
(b) Will the height of the water column in part (a) change if the cross section of the water column is made wider ?
The correct Answer is:(a) 9.52m
(b) No
To solve the problem step by step, let's break it down into two parts as given in the question.
Part (a): Calculate the height of a water column which will exert the same pressure as a 70 cm column of mercury.
1. Understand the formula for pressure:
The pressure exerted by a column of liquid is given by the formula:
P=ρ⋅g⋅h
where P is the pressure, ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
2. Identify the known values:
- Height of mercury column, hHg=70cm
- Density of mercury, ρHg=13.6g/cm3
- Density of water, ρwater=1g/cm3
3. Set up the equation:
Since we want the pressure exerted by the water column to equal the pressure exerted by the mercury column, we can set up the equation:
ρwater⋅g⋅hwater=ρHg⋅g⋅hHg
4. Cancel out g:
Since g is common on both sides, we can cancel it out:
ρwater⋅hwater=ρHg⋅hHg
5. Substitute the known values:
Substitute the values into the equation:
1⋅hwater=13.6⋅70
6. Calculate hwater:
hwater=13.6⋅70=952cm
Thus, the height of the water column that will exert the same pressure as a 70 cm column of mercury is 952 cm.
Part (b): Will the height of the water column in part (a) change if the cross-section of the water column is made wider?
1. Understand the concept of pressure:
The pressure exerted by a liquid column depends only on the height of the column and the density of the liquid, not on the cross-sectional area.
2. Conclusion:
Therefore, making the cross-section of the water column wider will not affect the height of the water column required to exert the same pressure. The height will remain 952 cm regardless of the cross-section.
Final Answers:
(a) The height of the water column is 952 cm.
(b) No, the height of the water column will not change if the cross-section is made wider.
The pressure exerted by a column of liquid is given by the formula:
P=ρ⋅g⋅h
where P is the pressure, ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
- Height of mercury column, hHg=70cm
- Density of mercury, ρHg=13.6g/cm3
- Density of water, ρwater=1g/cm3
Since we want the pressure exerted by the water column to equal the pressure exerted by the mercury column, we can set up the equation:
ρwater⋅g⋅hwater=ρHg⋅g⋅hHg
Since g is common on both sides, we can cancel it out:
ρwater⋅hwater=ρHg⋅hHg
Substitute the values into the equation:
1⋅hwater=13.6⋅70
hwater=13.6⋅70=952cm
The pressure exerted by a liquid column depends only on the height of the column and the density of the liquid, not on the cross-sectional area.
Therefore, making the cross-section of the water column wider will not affect the height of the water column required to exert the same pressure. The height will remain 952 cm regardless of the cross-section.
(a) The height of the water column is 952 cm.
(b) No, the height of the water column will not change if the cross-section is made wider.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREEXERCISE - Exercise-4(A)Assumptions4videos
PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSURE
- BOOK - ICSECHAPTER - PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREEXERCISE - Exercise -4(B)31videos
PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSURE
- BOOK - ICSECHAPTER - PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREEXERCISE - Exercise-4(A)multiple choice4videos
PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSURE
- BOOK - ICSECHAPTER - MOTION IN ONE DIMENSION EXERCISE - EXERCISE -2 (C) ( Multiple choice type :)17videos
MOTION IN ONE DIMENSION
- BOOK - ICSECHAPTER - PROPAGATION OF SOUND WAVES EXERCISE - EXERCISE -8(B) (Multiple choice type)3videos
PROPAGATION OF SOUND WAVES
Similar Questions
Will the height of the water column change if the cross section of the water column is made wider ?
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
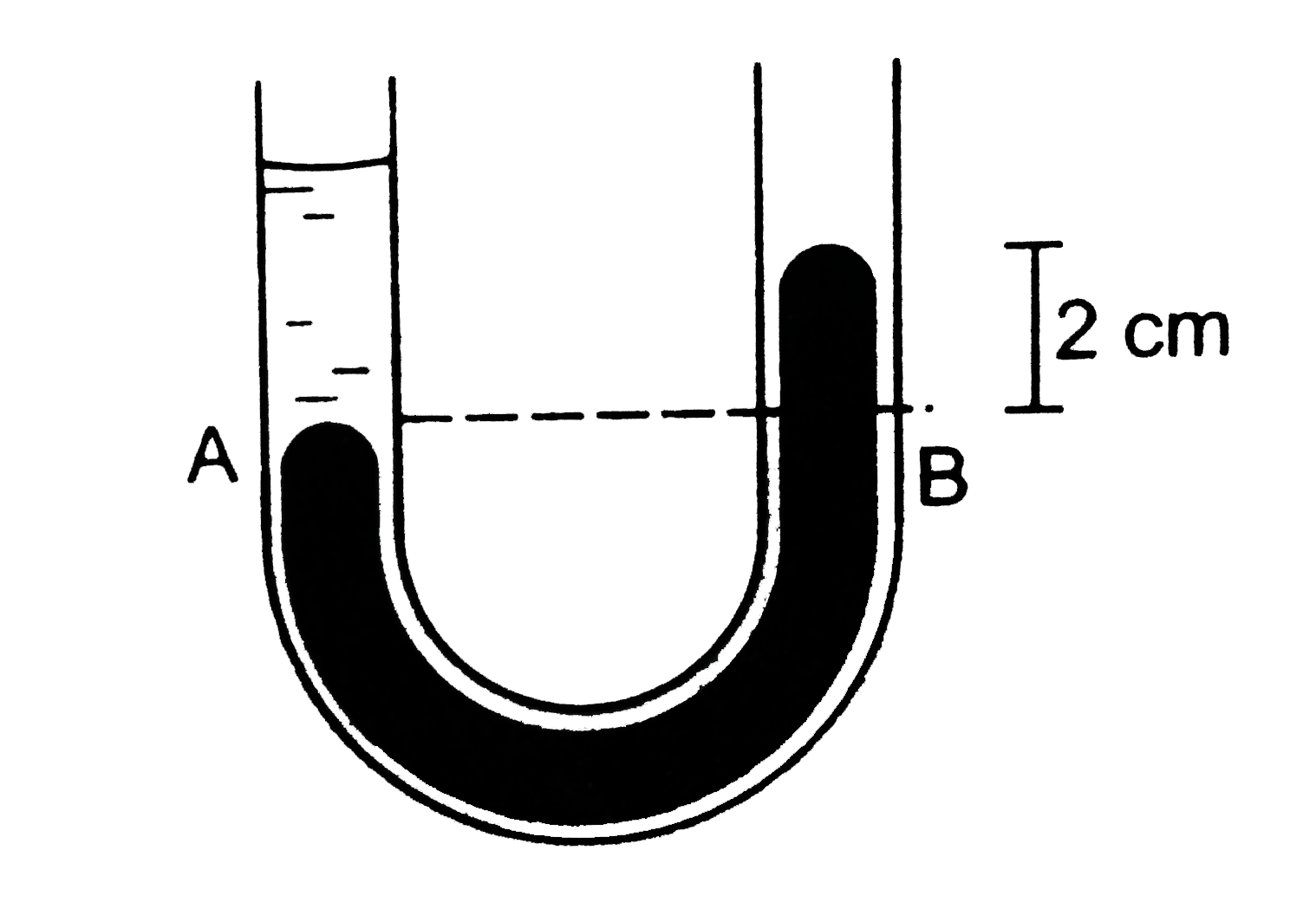 ,View Solution
,View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
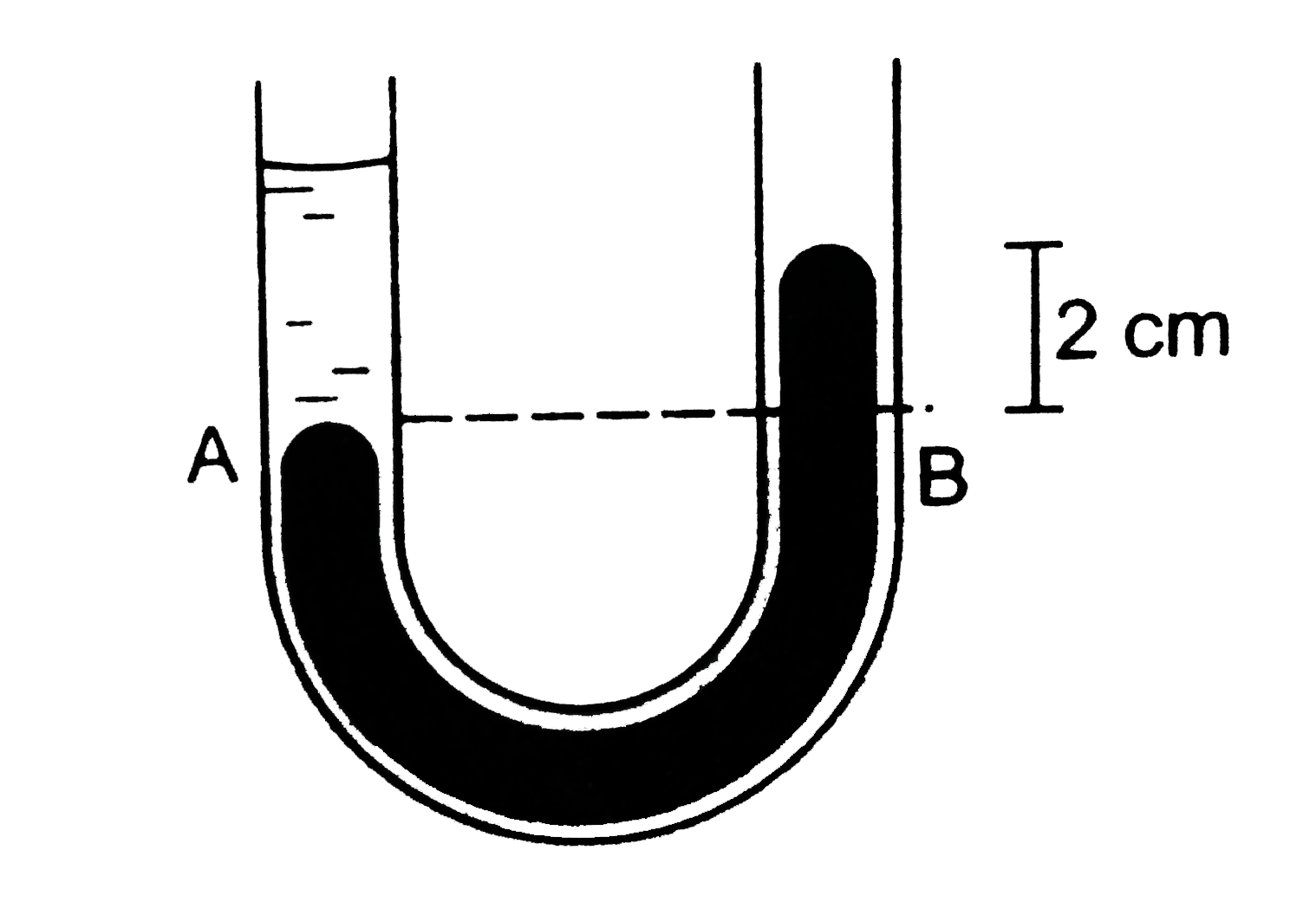 ,View Solution
,View SolutionExpress one atm pressure in terms of the height of mercury column.
View SolutionA U-shaped tube open to the air at both ends contains some mercury. A quantity of water is carefully poured into the left arm of the U-shaped tube until the vertical height of the water column is 15.0cm.
(a) What is the gauge pressure at the water mercury interface ?
(b) Calculate the vertical distance h from the top of the mercury in the right hand arm of the tube to the top of the water in the left-hand arm.
 .View Solution
.View SolutionExplain how is the height of mercury column in the tube of a simple barometer, a measure of the atmospheric pressure.
View SolutionWater rises to a height of 10 cm in capillary tube and mercury falls to a depth of 3.112 cm in the same capillary tube. If the density of mercury is 13.6 and the angle of contact for mercury is 135∘, the ratio of surface tension of water and mercury is
View SolutionThe column of mercury in a barometer is 76mm of Hg. Calculate the atmospheric pressure if the density of mercury = 13600kgm −3 . (Take g=10ms −2 )
View SolutionThe density of liquid mercury is 13.6g/cm3. How many moles of mercury are there in 1 litre of the metal? (Atomic mass of Hg=200).
View SolutionTorricelli's barometer used mercury. Pascal duplicated it using French wine of density 984kgm−3. Determine the height of the wine column for normal atmospheric pressure.
View Solution

