The human lungs can function satisfactorily up to a limit where the pressure difference between the outside and inside of the lungs is one -twentieth of an atmosphere . If a diver uses a snorkel for breathing , how for below the water can she swim ? Assume the diver is in salt water whose density is 1025kg/m3 .
0.25 m
0.35 m
0.50 m
0.20 m
The correct Answer is:C
To solve the problem of how deep a diver can swim while using a snorkel, we need to analyze the pressure differences involved. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the pressure difference limit
The problem states that the human lungs can function satisfactorily up to a pressure difference of one-twentieth of an atmosphere.
ΔP=120×Patm
Where Patm is the atmospheric pressure, approximately 1.013×105Pa.
Step 2: Calculate the maximum pressure difference in Pascals
Substituting the value of atmospheric pressure into the equation gives:
ΔP=120×1.013×105Pa=1.013×10520Pa
Calculating this:
ΔP=5065Pa
Step 3: Relate pressure difference to depth
As the diver goes deeper into the water, the pressure increases due to the weight of the water above. The pressure at a depth h in a fluid is given by:
P=ρgh
Where:
- ρ is the density of the salt water (given as 1025kg/m3),
- g is the acceleration due to gravity (approximately 9.8m/s2),
- h is the depth in meters.
Step 4: Set up the equation for pressure difference
The pressure difference that the diver experiences as they go deeper should equal the maximum pressure difference that their lungs can handle:
ρgh=5065Pa
Step 5: Substitute known values into the equation
Substituting the values of ρ and g:
1025kg/m3×9.8m/s2×h=5065Pa
Step 6: Solve for h
Rearranging the equation to solve for h:
h=5065Pa1025kg/m3×9.8m/s2
Calculating the denominator:
1025×9.8≈10045kg/(m2s2)
Now substituting back into the equation for h:
h=506510045≈0.504m
Step 7: Final result
Thus, the diver can swim approximately:
h≈0.5m
Conclusion
The maximum depth the diver can swim while using a snorkel is approximately 0.5 meters.
---
The problem states that the human lungs can function satisfactorily up to a pressure difference of one-twentieth of an atmosphere.
Substituting the value of atmospheric pressure into the equation gives:
As the diver goes deeper into the water, the pressure increases due to the weight of the water above. The pressure at a depth h in a fluid is given by:
- ρ is the density of the salt water (given as 1025kg/m3),
- g is the acceleration due to gravity (approximately 9.8m/s2),
- h is the depth in meters.
The pressure difference that the diver experiences as they go deeper should equal the maximum pressure difference that their lungs can handle:
Substituting the values of ρ and g:
Rearranging the equation to solve for h:
Thus, the diver can swim approximately:
The maximum depth the diver can swim while using a snorkel is approximately 0.5 meters.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )10videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Linked Comprehension )9videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PROBLEMS68videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELECTROMAGNETIC WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
Similar Questions
The maximum depth dmax that a diver can snorkel is set by the density of the water and the fact that human lungs can function against a maximum pressure difference between inside and outside the chest cavity) of 0.050 atm. What is the difference in dmax for fresh water and the water of the Dead Sea (the saltiest natural water in the world, with a density of 1.5x103kg/m3)?
View SolutionSnorkeling by humans and elephants. When a person snorkels, the lungs are connected directly to the atmosphere through the snorkel tube and thus are at atmospheric pressure. In atmospheres, what is the difference Δp between this internal air pressure and the water pressure against the body if the length of the snorkel tube is (a) 20 cm (standard situation) and (b) 3.5 m (probably lethal situation)? In the latter, the pressure difference causes blood vessels on the walls of the lungs to rupture, releasing blood into the lungs. As depicted in Fig. 14-52, an elephant can safely snorkel through its trunk while swimming with its lungs 3.5 m below the water surface because the membrane around its lungs contains connective tissue that holds and protects the blood vessels, preventing rupturing.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Swimming is an interesting sport, and one that relaxes us also. Normally and average human being would drown in water.As a person goes inside water , the water exert a force on it in upwared direction. This force is called buyont froce. The force is given by V dg, where d is density of water, V is volume of body inside water and g is acceleration due to gravity. normally, this force is lesser than this weight. so the man pushes water to get an additional force on himself. this effort is known as swimming. assume water has a density of 1000kg/m3
A man of mass 50 kg has a volume of 0.045m3. how much force should be apply on water to just stay afloat?A50 N downB50 N upC100 N downD10 0 N up - Question 2 - Select One
Swimming is an interesting sport, and one that relaxes us also. Normally and average human being would drown in water.As a person goes inside water , the water exert a force on it in upwared direction. This force is called buyont froce. The force is given by V dg, where d is density of water, V is volume of body inside water and g is acceleration due to gravity. normally, this force is lesser than this weight. so the man pushes water to get an additional force on himself. this effort is known as swimming. assume water has a density of 1000kg/m3
By how many m3 should man increase his volume (by inflating his lungs) so that he can stay afloat without applying any force on waterA0.005m3B0.004m3C0.003m3D0.001m3 - Question 3 - Select One
Swimming is an interesting sport, and one that relaxes us also. Normally and average human being would drown in water.As a person goes inside water , the water exert a force on it in upwared direction. This force is called buyont froce. The force is given by V dg, where d is density of water, V is volume of body inside water and g is acceleration due to gravity. normally, this force is lesser than this weight. so the man pushes water to get an additional force on himself. this effort is known as swimming. assume water has a density of 1000kg/m3
If a sphere is resting on the ocean floor, its free body diagram would beA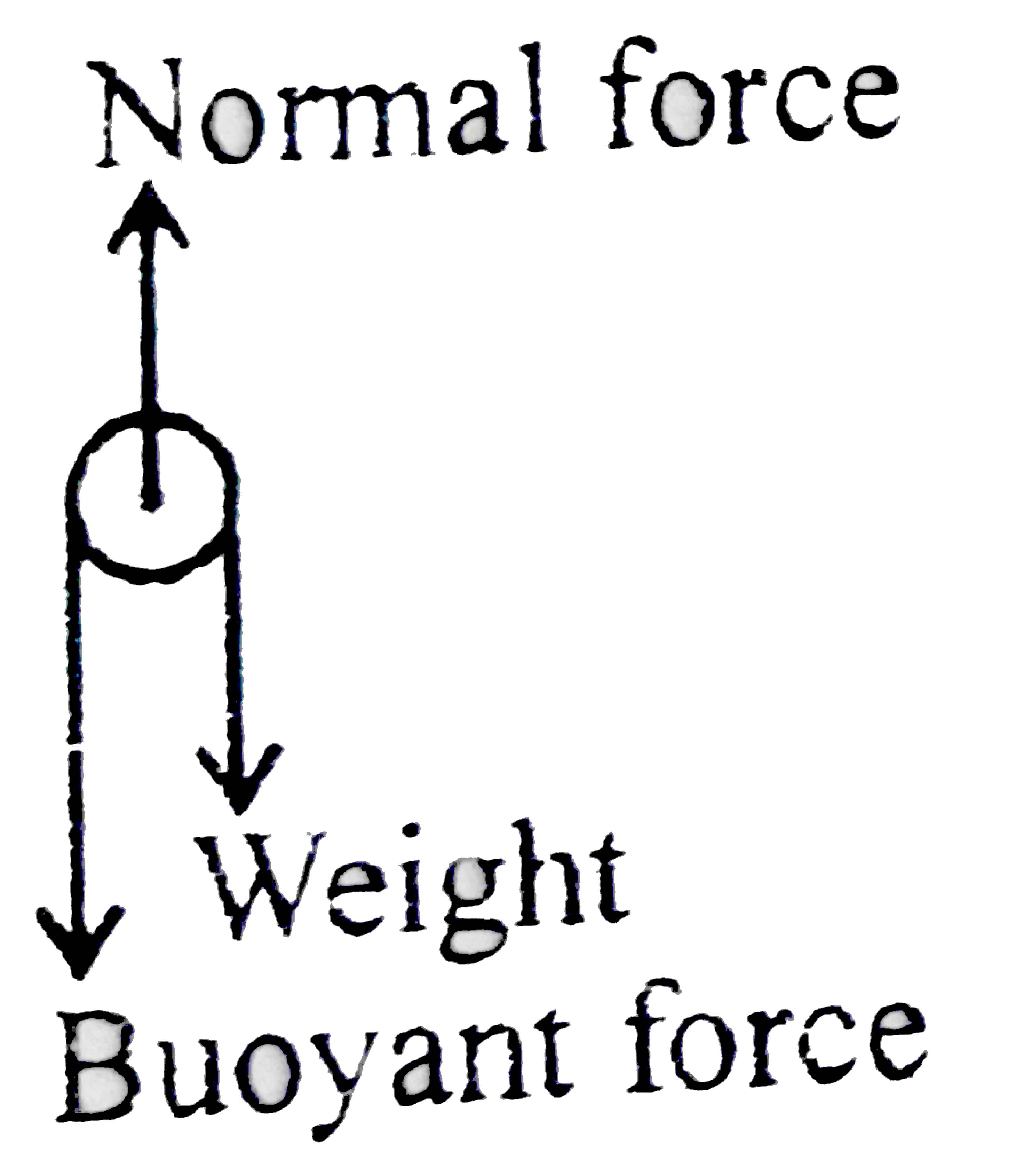 B
B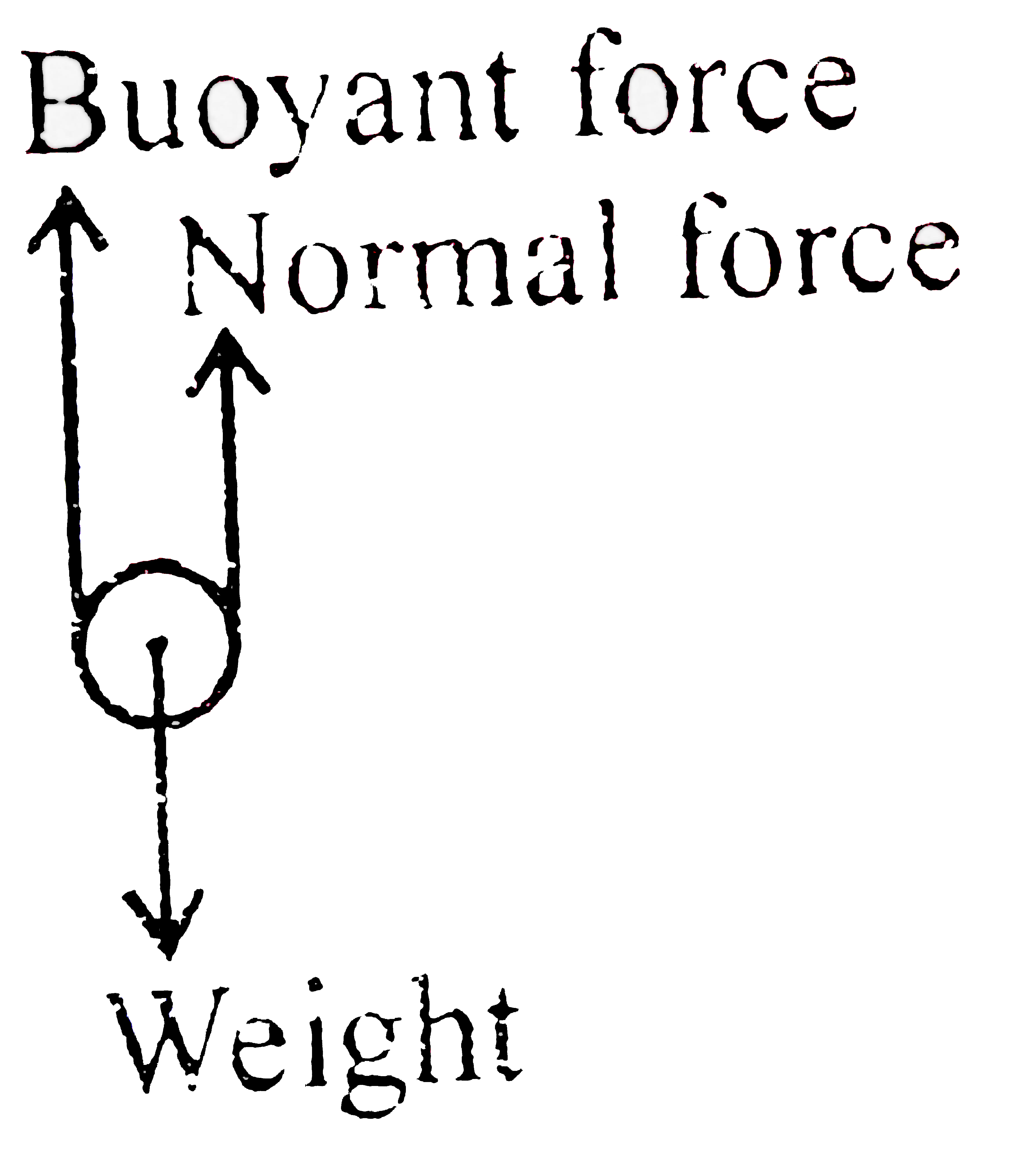 C
C D
D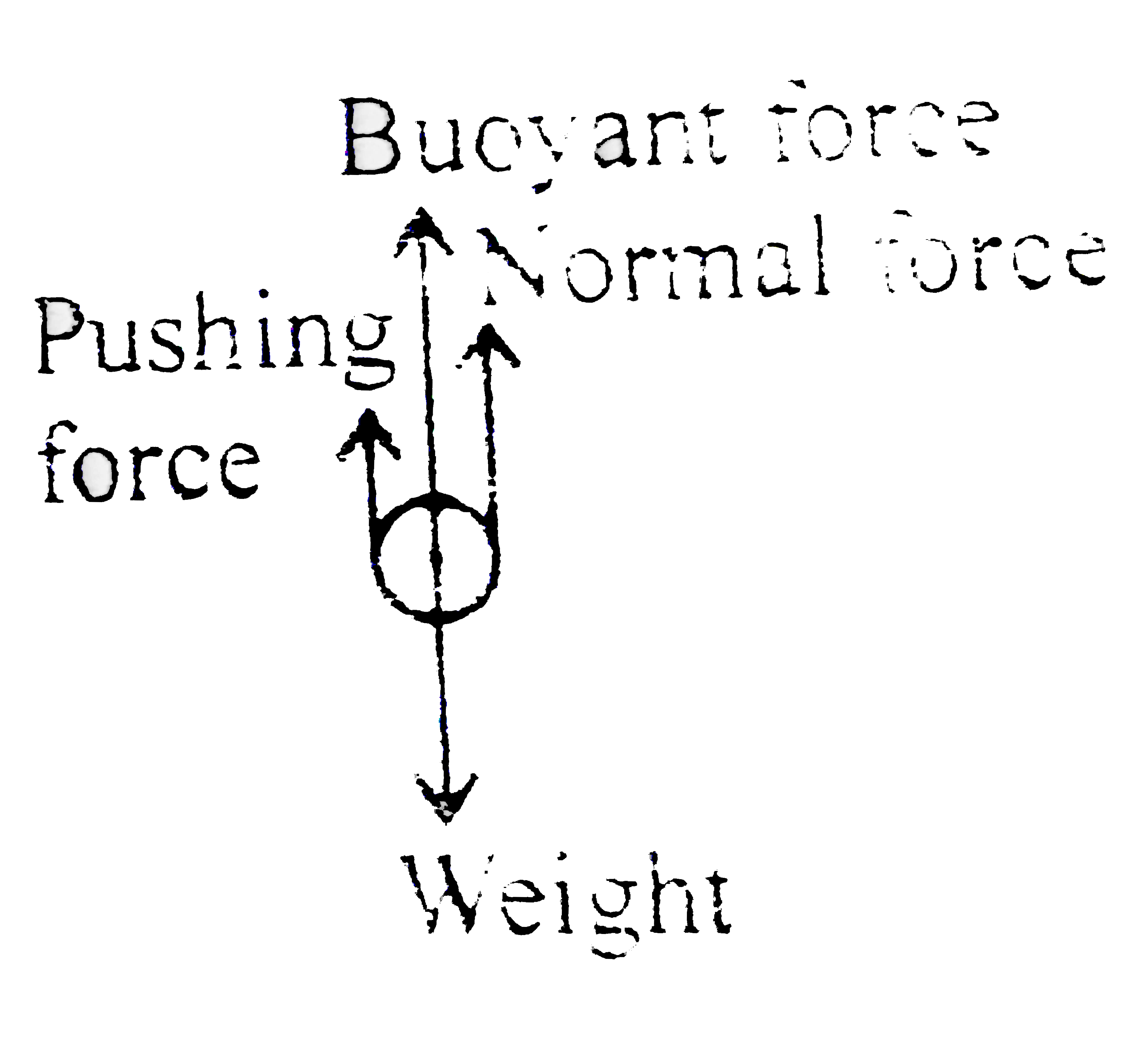
A cylindrical furnace has height (H) and diameter (D) both 1 m. It is maintained at temperature 360 K. The air gets heated inside the furnace at constant pressure P_α, and its temperature becomes T = 360K The hot air with density ρ rises up a vertical chimney of diameter d = 0.1 m and height h = 9 m above the furnace and exits the chimney (see the figure). As a result, atmospheric air of density ρα=1.2kgm−3, pressure Pα, and temperature Tα = 300K enters the furnace. Assume air as an ideal gas, neglect the variations in ρ and T inside the chimney and the furnace. Also ignore the viscous effects.
[Given: The acceleration due to gravity g = 10ms−2 and π = 3.14 ]
When the chimney is closed using a cap at the top, a pressure difference ΔP develops between the top and the bottom surfaces of the cap. If the changes in the temperature and density of the hot air, due to the stoppage of air flow, are negligible then the value of ΔP is _________Nm^(-2)View SolutionWater is used as the manometric liquid in a pitot tube mounted in an aircraft to measure air speed. If the maximum difference in height between the liquid columns is 0.1m, what is the maximum air speed that can be measured? Density of air ddir=1.3kg/m3
View SolutionAn open rectangular tank 5mxx4mxx3m in dimension is containing water up to a height of 2m the tank is accelerated horizontally along the longer side. Assuming water to be and ideal liquid find-
(a) the maximum acceleration with which the tank can be moved so that water does not fall from the rear side.
(b) the gauge pressure at the bottom of the front and back of the tank (points A and B) if the tank is closed at the top and is then acclerated horizontally at 9m/s2. Assume that the top cover has a small hole at the right side of the tank so taht pressure of air inside the tank is maintained at atmospheric pressure. Gauge pressure at a point is difference in absolute pressure at the point and atmospheric pressure.
 View Solution
View SolutionCalculate the work associated with the vaporization of 1 mol of water is 373K and 1 atm. Assume ideal gas behavior.
Strategy : As liquid water absorbs heat, it forms vapor 1 atm pressure. As the amount of vapor increases, the piston rises. The value of ΔV is the difference in volume between the initial and final states of the system. The final volume is the volume of one mole of water vapor at the secified conditions. We can find by using the ideal gas equaition (PV=nRT). The initial volume of 1 mol of liquid water [V=d.m=(1gmL−1)(18g)=18mL] is negligible relative to the volume of water vapor. In general the volume of liquid or solid can be neglected in the calculation of ΔV because they are so much smaller the the volume of the same amount of gas.View SolutionRead the passage given below and answer the following questions :
Scuba apparatus includes a tank of compressed air toted by the diver on his or her back, a hose for carrying air to a mouthpiece, a face mask that covers the eyes and nose, regulators that control air flow, and gauges that indicate depth and how much air remains in the tank. A diver who stays down too Iong swims too deep or comes up too fast can end up with a condition called 'the bends." In this case, bubbles of gas in the blood can cause intense pain, even death.
In these following questions a statement of assertion followed by a statement of reason is given. Choose the correct answer out of the following choices
Assertion : Soft drinks and soda water bottles are sealed under high pressure.
Reason : High pressure maintains the taste and texture of the soft drinks.View Solution

