The instaneous velocity of point B of the given rod of length 0.5 is 3m/s in the represented direction. The angualr velocity of the rod for minimum velocity of end A is
1.5 rad/s
5.2 rad/s
2.5 rad/s
3.6 rad/s
b) if rod is rotated about end A, then vertical component of velocity, v⊥ of end A will be zero.
∴ ω=(vsin60∘)/l=(sqrt(3)v)/(2l) = (sqrt(3) xx 3)/(2 xx 0.5) = 5.2 rad/s
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - BITSAT GUIDECHAPTER - ROTATIONAL MOTIONEXERCISE - BITSAT Archives
9 Videos
- NEWTONS LAWS OF MOTION AND FRICTIONBOOK - BITSAT GUIDECHAPTER - NEWTONS LAWS OF MOTION AND FRICTIONEXERCISE - BITSAT Archives
23 Videos
- SCALARS AND VECTORSBOOK - BITSAT GUIDECHAPTER - SCALARS AND VECTORSEXERCISE - All Questions
34 Videos
Similar Questions
A rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.
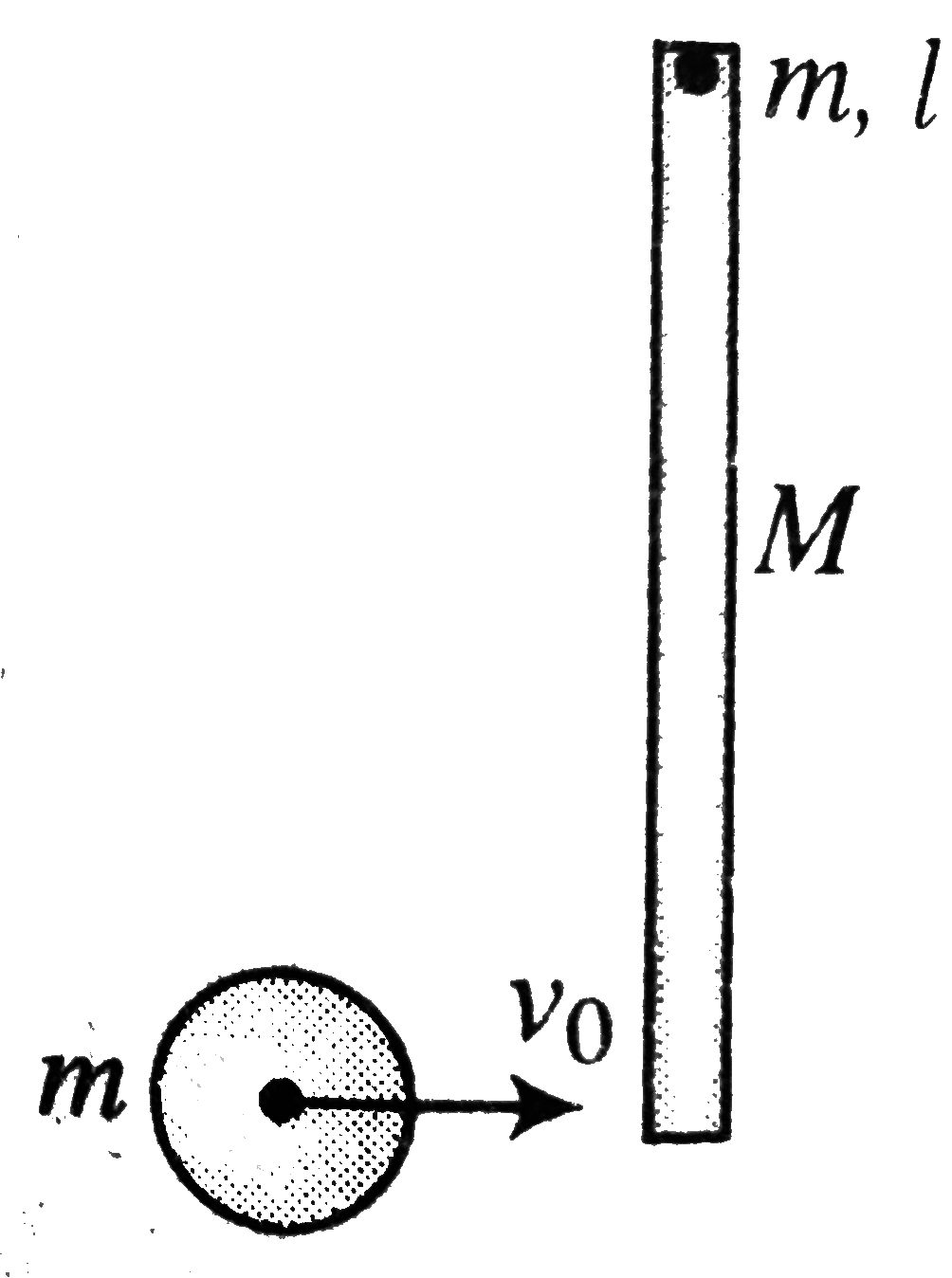
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View Solution
Knowledge Check
In the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be
Av2LBvLCv√32LDnone of theseThe velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
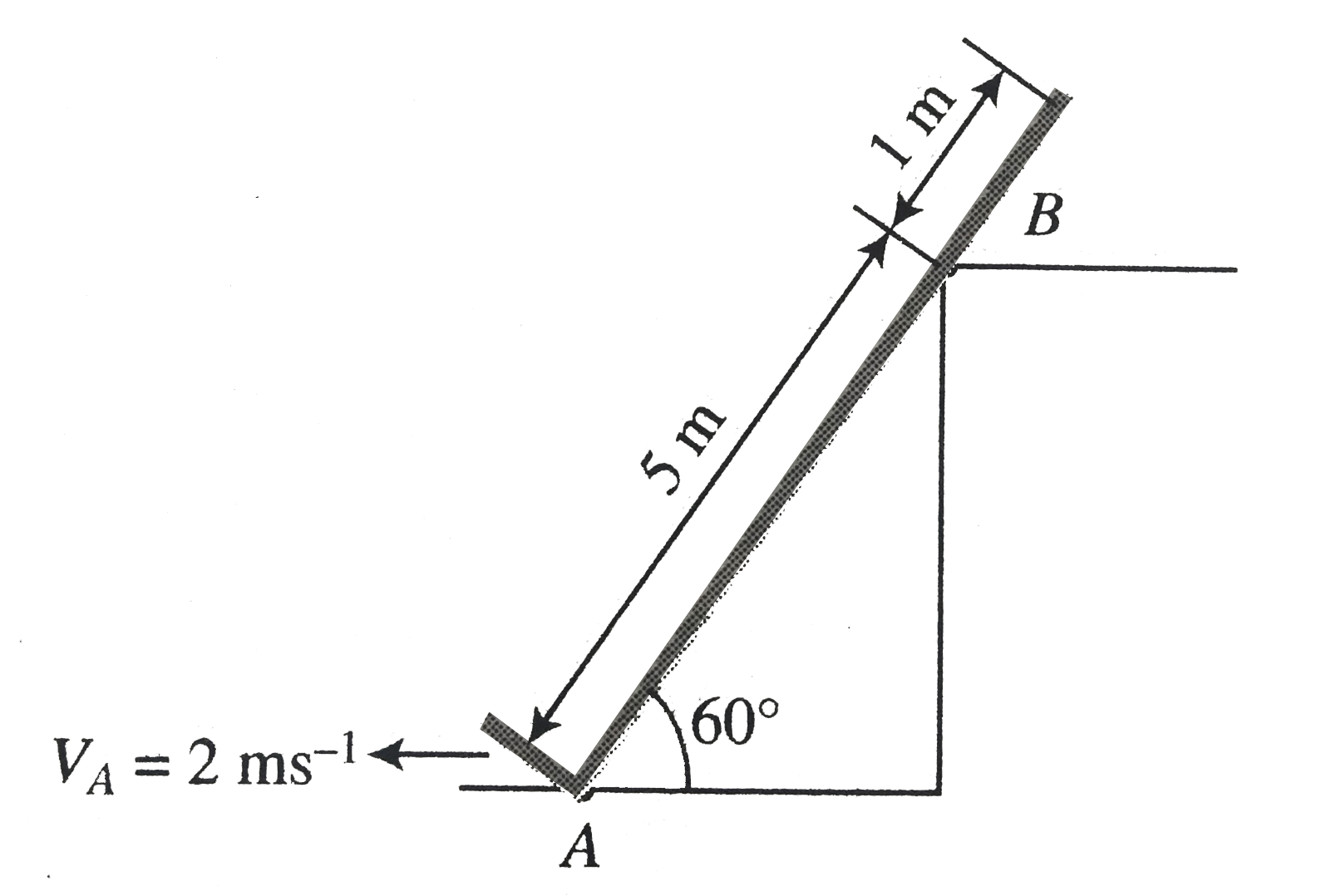A2√3ms−1B1ms−1C12√3ms−1D√32ms−1A rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
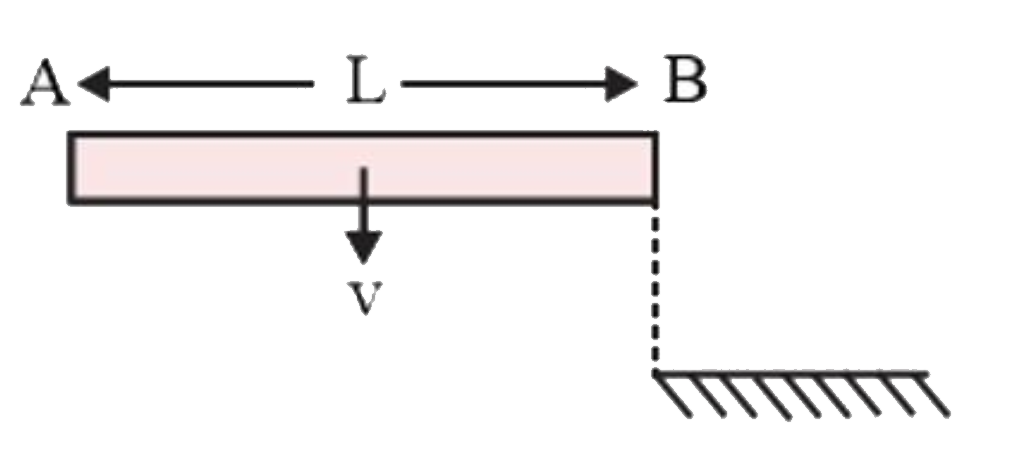Av2LB3vLC3v2LDvL
A rigid horizontal smooth rod AB of mass 0.75kg and length 40cm can roate freely about a fixed vertical axis through its mid point O. Two rings each of mass 1kg are initially at rest at a distance of 10cm from O on either side of the rod. The rod is set in rotatiob with an angular velocity of 30 radians per second. Find the velocity of each ring along the length of the rod in m/s when they reach the ends of the rod.
.
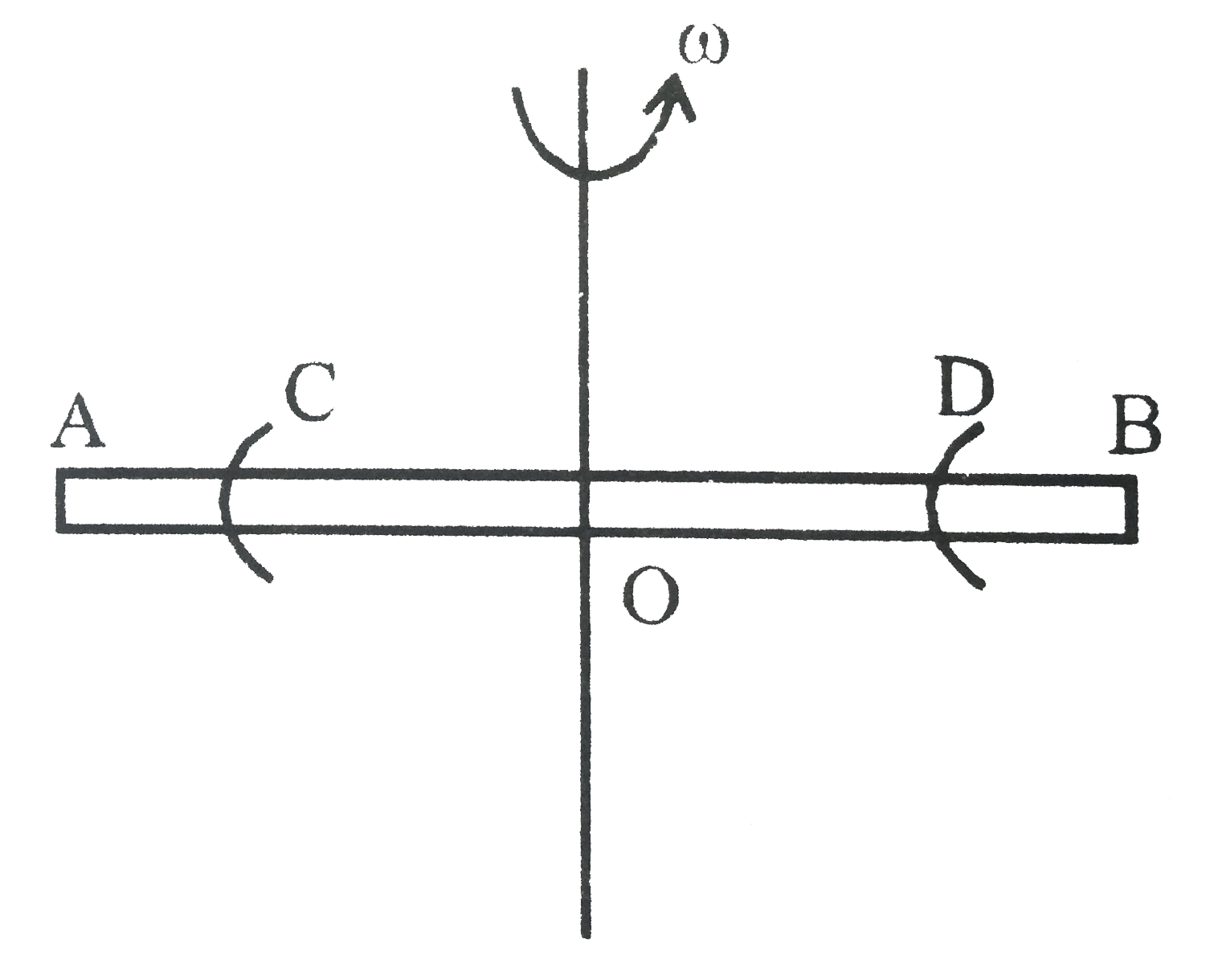View SolutionA small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
View Solution
Rod AB has length L. velocity of end A of the rod has velocity υ0 at the given instant.
(a). Which type of motion the rod has?
(b). Find velocity of end B at the given instant.
(C). Find the angular velocity of the rod.
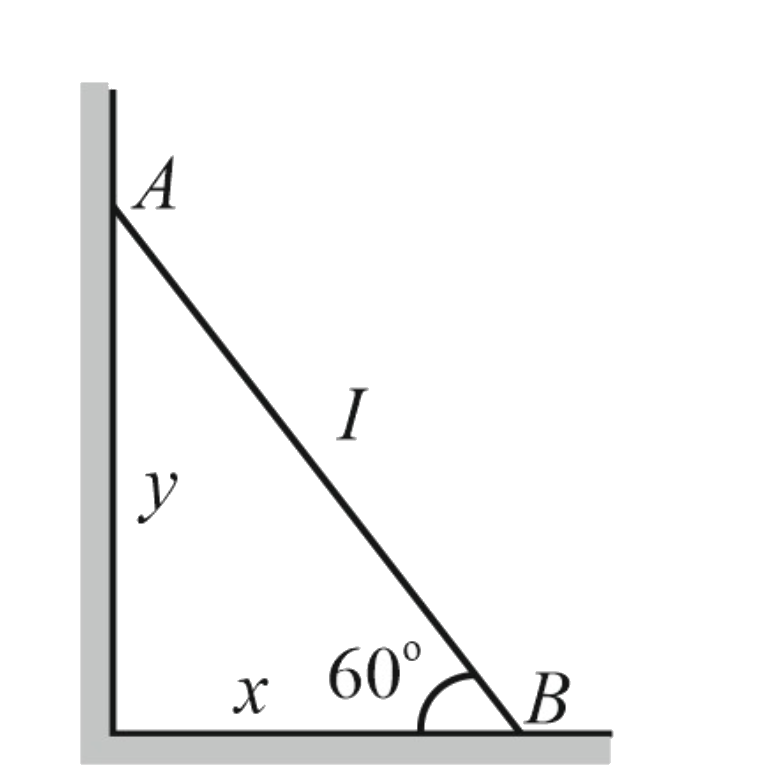
View SolutionA rod length AB is moving with ends remaining in contact with frictionless wall and floor . If at the instant shown , the velocity of the and B is 3ms−1 towards the negative x-direction , then the magnitude of the velocity of the end A wll be
View SolutionA mechanism consists of a part which is translated with a velocity u and a rod AB of length L and mass M hinged at A The rod rotates about axis A with angular velocity ω the kinetic energy of rod when it is vertical as shown is
View Solution