The internal surface of the walls of a sphere is specular. The radius of the sphere is R=36cm. A point source S is placed at a distance R/2 from the cneter of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflections from the remote and then nearest wall of the sphere? How will the position of the image change if the source sends light to the nearest wall first?Consider paraxial rays.
The correct Answer is:Image will be at −5R6 from near end towards source;
image will be at −R2 from remote end
To solve the problem, we will analyze the situation step by step, considering the reflections from the walls of the sphere.
Given:
- Radius of the sphere, R=36cm
- Distance of the point source S from the center of the sphere, d=R2=18cm
Step 1: Identify the positions
1. The center of the sphere is at point O.
2. The source S is located at a distance of 18cm from O towards one side of the sphere.
Step 2: Determine the distances for the remote wall reflection
1. The distance from the source S to the remote wall of the sphere (the wall opposite to the source) is:
dremote=R−d=36cm−18cm=18cm
2. The object distance u for the remote wall (considering the sign convention) is:
u=−dremote=−18cm
Step 3: Calculate the image position after the first reflection (remote wall)
1. The focal length f of the concave mirror (remote wall) is:
f=−R2=−18cm
2. Using the mirror formula:
1v−1u=1f
Substituting the values:
1v−1−18=1−18
This simplifies to:
1v+118=−118
1v=−218=−19
Therefore, the image distance v is:
v=−9cm
This means the image is located 9cm from the center of the sphere towards the source.
Step 4: Determine the distances for the nearest wall reflection
1. The distance from the image (after the first reflection) to the nearest wall is:
dnearest=R−|v|=36cm−9cm=27cm
2. The object distance u for the nearest wall (considering the sign convention) is:
u=−dnearest=−27cm
Step 5: Calculate the image position after the second reflection (nearest wall)
1. The focal length f of the nearest wall (concave mirror) is:
f=−R2=−18cm
2. Using the mirror formula again:
1v−1u=1f
Substituting the values:
1v−1−27=1−18
This simplifies to:
1v+127=−118
1v=−118−127
Finding a common denominator (54):
1v=−354−254=−554
Therefore, the image distance v is:
v=−545≈−10.8cm
This means the final image position is approximately 10.8cm from the center of the sphere towards the source.
Step 6: Change in image position if the source sends light to the nearest wall first
1. If the source sends light to the nearest wall first, the image will be formed at infinity since the source is at the focal point of the concave mirror.
2. The image will then reflect back to the remote wall, which will create an image at the center of the sphere.
Summary of Results:
- First Case (Remote Wall then Nearest Wall): Final image position is approximately 10.8cm from the center towards the source.
- Second Case (Nearest Wall then Remote Wall): Final image position is at the center of the sphere.
- Radius of the sphere, R=36cm
- Distance of the point source S from the center of the sphere, d=R2=18cm
1. The center of the sphere is at point O.
2. The source S is located at a distance of 18cm from O towards one side of the sphere.
1. The distance from the source S to the remote wall of the sphere (the wall opposite to the source) is:
dremote=R−d=36cm−18cm=18cm
2. The object distance u for the remote wall (considering the sign convention) is:
u=−dremote=−18cm
1. The focal length f of the concave mirror (remote wall) is:
f=−R2=−18cm
2. Using the mirror formula:
1v−1u=1f
Substituting the values:
1v−1−18=1−18
This simplifies to:
1v+118=−118
1v=−218=−19
Therefore, the image distance v is:
v=−9cm
This means the image is located 9cm from the center of the sphere towards the source.
1. The distance from the image (after the first reflection) to the nearest wall is:
dnearest=R−|v|=36cm−9cm=27cm
2. The object distance u for the nearest wall (considering the sign convention) is:
u=−dnearest=−27cm
1. The focal length f of the nearest wall (concave mirror) is:
f=−R2=−18cm
2. Using the mirror formula again:
1v−1u=1f
Substituting the values:
1v−1−27=1−18
This simplifies to:
1v+127=−118
1v=−118−127
Finding a common denominator (54):
1v=−354−254=−554
Therefore, the image distance v is:
v=−545≈−10.8cm
This means the final image position is approximately 10.8cm from the center of the sphere towards the source.
1. If the source sends light to the nearest wall first, the image will be formed at infinity since the source is at the focal point of the concave mirror.
2. The image will then reflect back to the remote wall, which will create an image at the center of the sphere.
- First Case (Remote Wall then Nearest Wall): Final image position is approximately 10.8cm from the center towards the source.
- Second Case (Nearest Wall then Remote Wall): Final image position is at the center of the sphere.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Single Correct221videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.721videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
View SolutionA point charge q , is placed at a distance r from the centre of an aluminium sphere, of radius R (r>R) . Selectr the correct alternatives.
 View Solution
View SolutionA hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10V. The potential at the distance 3cm from the centre of the sphere is:
View SolutionFind the radius of the sphere whose surface area is 36πcm2.
View SolutionThe diameter of a hollow metallic sphere is 60 cm and the sphere carries a charge of 500μC. The potential at a distance of 100cm from the centre of the sphere will be
View SolutionA point object is situated at a distance of 36 cm from the centre of the sphere of radius 12 cm and refractive index 1.5. Locate the position of the image due to refraction through sphere.
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :
 View Solution
View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
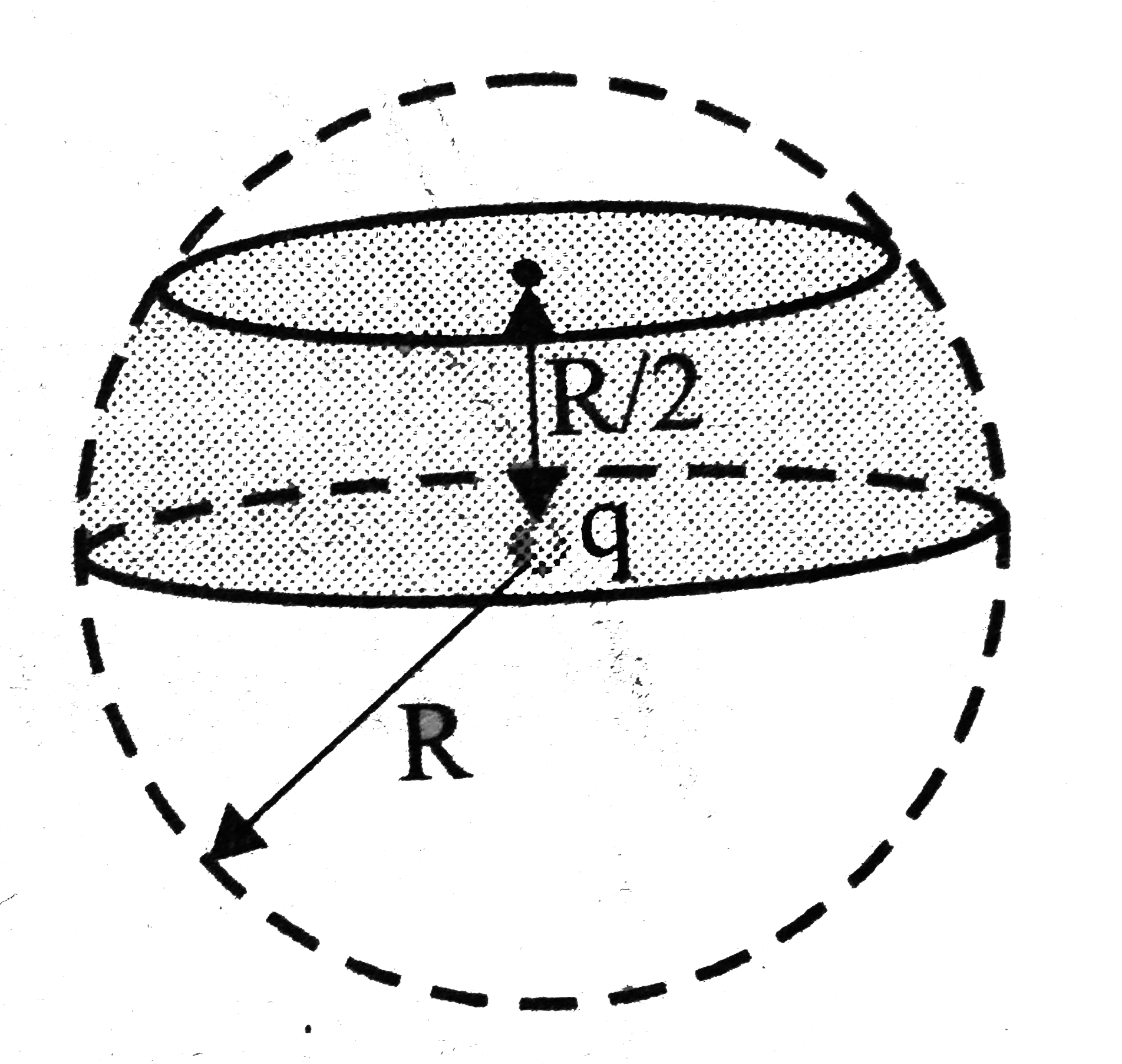
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
 View Solution
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View Solution
