A parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
32
53
2
52
The correct Answer is:C
To solve the problem, we need to determine the refractive index (μ1) of the sphere when a point source of light is placed at its surface and a parallel beam of light emerges from the opposite surface.
1. Understanding the Setup:
- We have a sphere with a point source of light at its surface.
- A parallel beam of light emerges from the opposite surface of the sphere.
2. Using the Refraction Formula:
- The general equation for refraction at a spherical surface is given by:
μ2V−μ1U=μ2−μ1R
- Here, μ2 is the refractive index of air (which is 1), μ1 is the refractive index of the sphere, R is the radius of the sphere, U is the object distance, and V is the image distance.
3. Assigning Values:
- Since the point source is at the surface of the sphere, the object distance U=−2R (negative because it is on the same side as the incoming light).
- The image distance V is considered to be at infinity because the light emerges as a parallel beam.
4. Substituting Values into the Formula:
- Substitute μ2=1, V=∞, and U=−2R into the refraction formula:
1∞−μ1−2R=1−μ1R
- Since 1∞=0, the equation simplifies to:
0+μ12R=1−μ1R
5. Eliminating R:
- Multiply through by R to eliminate the radius:
μ12=1−μ1
6. Rearranging the Equation:
- Rearranging gives:
μ1+μ12=1
- This can be rewritten as:
3μ12=1
7. Solving for μ1:
- Multiply both sides by 23:
μ1=23
8. Conclusion:
- The refractive index μ1 of the sphere is 2.
Final Answer:
The refractive index of the sphere is μ1=2.
- We have a sphere with a point source of light at its surface.
- A parallel beam of light emerges from the opposite surface of the sphere.
- The general equation for refraction at a spherical surface is given by:
μ2V−μ1U=μ2−μ1R
- Here, μ2 is the refractive index of air (which is 1), μ1 is the refractive index of the sphere, R is the radius of the sphere, U is the object distance, and V is the image distance.
- Since the point source is at the surface of the sphere, the object distance U=−2R (negative because it is on the same side as the incoming light).
- The image distance V is considered to be at infinity because the light emerges as a parallel beam.
- Substitute μ2=1, V=∞, and U=−2R into the refraction formula:
1∞−μ1−2R=1−μ1R
- Since 1∞=0, the equation simplifies to:
0+μ12R=1−μ1R
- Multiply through by R to eliminate the radius:
μ12=1−μ1
- Rearranging gives:
μ1+μ12=1
- This can be rewritten as:
3μ12=1
- Multiply both sides by 23:
μ1=23
- The refractive index μ1 of the sphere is 2.
The refractive index of the sphere is μ1=2.
Topper's Solved these Questions
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.4
15 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.5
13 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.2
15 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type
4 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
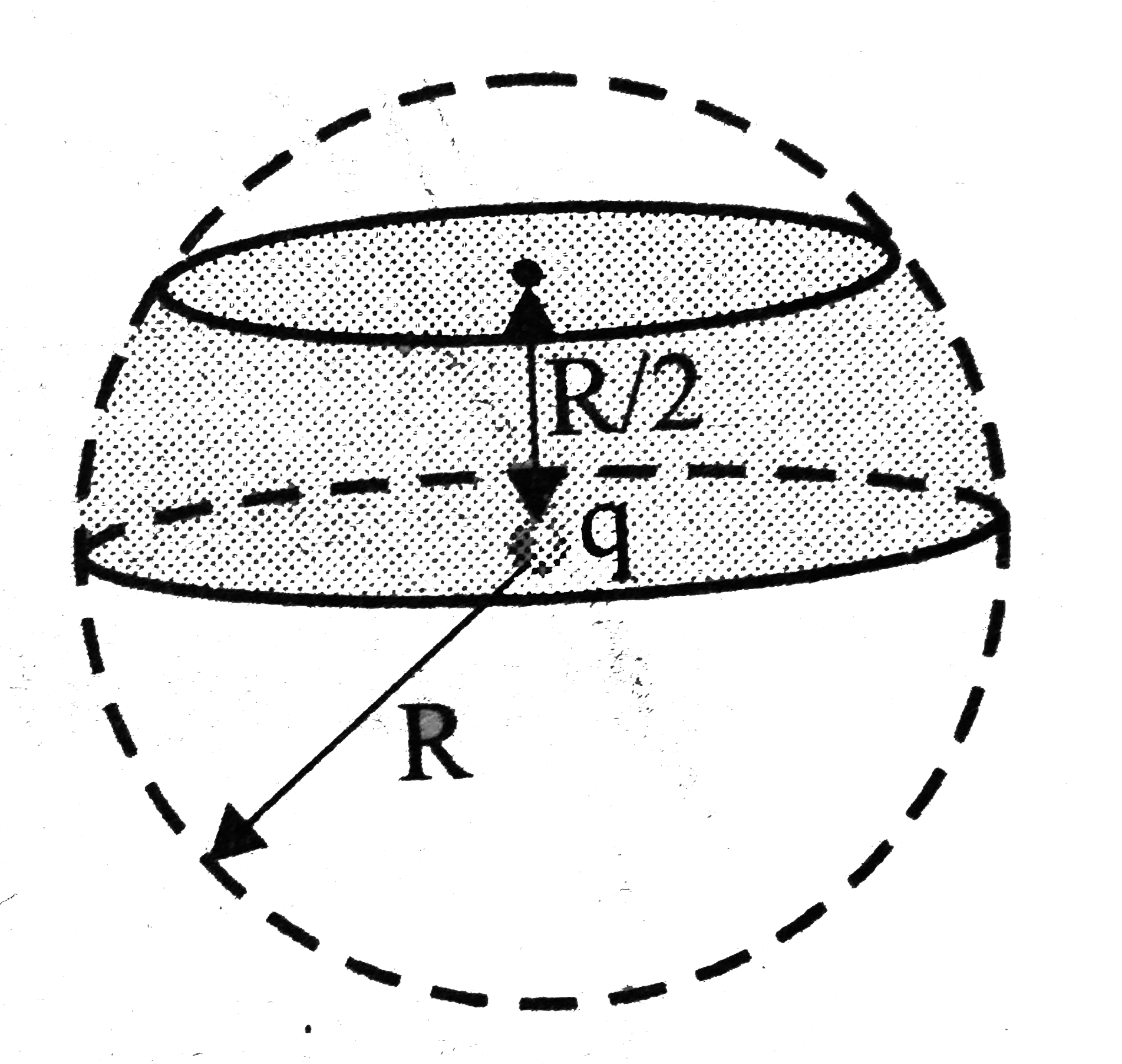
Flux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionA chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View SolutionA parallel beam of light falls on a solid tranparent sphere.
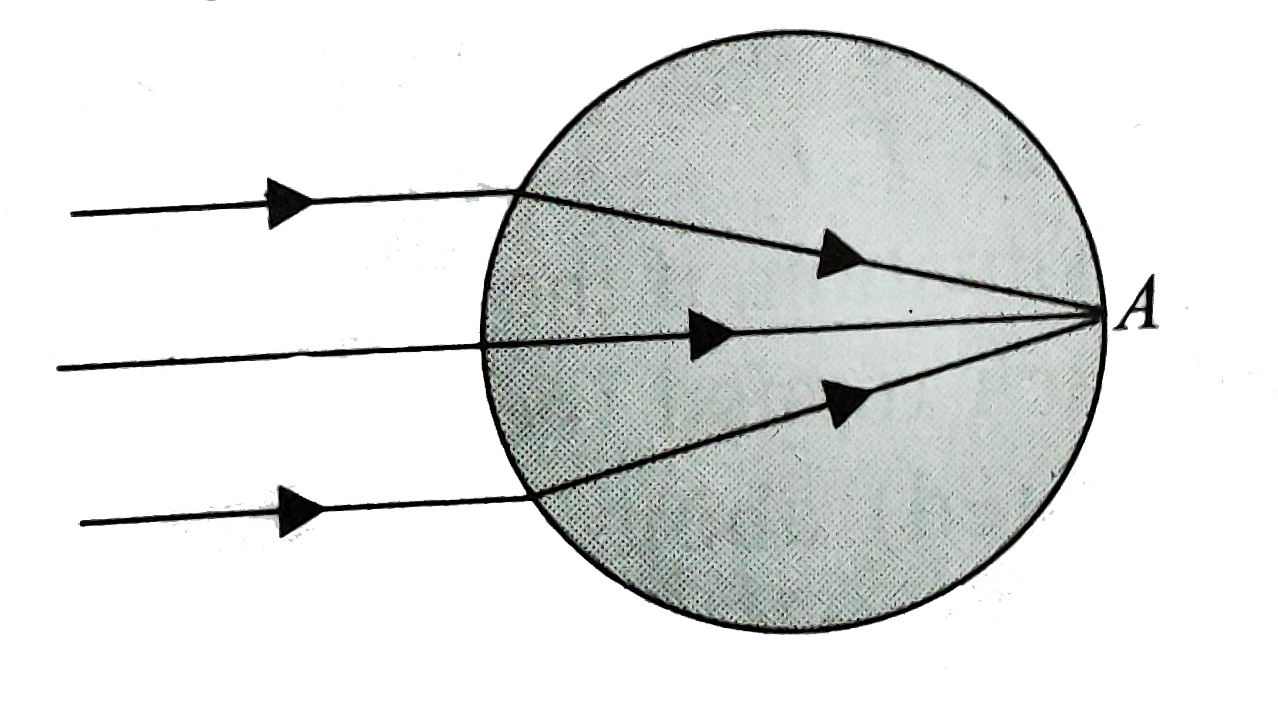
Q. Which is corret?
View SolutionAn object is at a distance of d=2.5cm from the surface of a glass sphere with a radius R=10cm. Find the position of the final image produced by the sphere. The refractive index of glass is μ=1.5.
View SolutionIf a charge is enclosed by the surface of the sphere then total flux emitted from the surface will be:
View SolutionA point source of light is placed at the bottom of a water lake. If the area of the illuminated circle on the surface is equal to 3 times the square of the depth of the lake. The refractive index of water is
View SolutionIn a prism of small angle A, a beam of light is incident on its surface at an angle of incidence i and leaves the opposite surface of it is angle of 90∘ with the surface. If prism material has refractive index of m then the value of angle of incidence will be:
View Solution
