The kinetic energy acquired by a mass m travelling a certain distance d, starting from rest, under the action of a force F such that the force F is directly proportional to t is
(a) Directly proportional to t2
(b) Independent of t
(c) Directly proportional to t4
(d) Directly proportional to t
The correct Answer is:C
To solve the problem of finding the kinetic energy acquired by a mass m traveling a distance d under the action of a force F that is directly proportional to time t, we can follow these steps:
Step 1: Establish the relationship between force and time
Given that the force F is directly proportional to time t, we can express this as:
F=kt
where k is a constant of proportionality.
Step 2: Relate force to acceleration
From Newton's second law, we know that force can also be expressed as:
F=mdvdt
Setting the two expressions for force equal gives:
mdvdt=kt
Step 3: Rearrange and integrate
We can rearrange the equation to separate variables:
mdv=ktdt
Now, we integrate both sides. The left side integrates with respect to v and the right side with respect to t:
∫mdv=∫ktdt
This gives:
mv=kt22+C
Since the mass starts from rest, when t=0, v=0, thus C=0. Therefore:
mv=kt22
Step 4: Solve for velocity v
Now we can solve for v:
v=kt22m
Step 5: Calculate kinetic energy
The kinetic energy KE is given by the formula:
KE=12mv2
Substituting the expression for v:
KE=12m(kt22m)2
This simplifies to:
KE=12m⋅k2t44m2=k2t48m
Step 6: Determine the relationship of kinetic energy with time
From the expression KE=k2t48m, we can see that kinetic energy is directly proportional to t4:
KE∝t4
Final Answer
Thus, the kinetic energy acquired by the mass m is directly proportional to t4.
---
Given that the force F is directly proportional to time t, we can express this as:
F=kt
where k is a constant of proportionality.
From Newton's second law, we know that force can also be expressed as:
F=mdvdt
Setting the two expressions for force equal gives:
mdvdt=kt
We can rearrange the equation to separate variables:
mdv=ktdt
Now, we integrate both sides. The left side integrates with respect to v and the right side with respect to t:
∫mdv=∫ktdt
This gives:
mv=kt22+C
Since the mass starts from rest, when t=0, v=0, thus C=0. Therefore:
mv=kt22
Now we can solve for v:
v=kt22m
The kinetic energy KE is given by the formula:
KE=12mv2
Substituting the expression for v:
KE=12m(kt22m)2
This simplifies to:
KE=12m⋅k2t44m2=k2t48m
From the expression KE=k2t48m, we can see that kinetic energy is directly proportional to t4:
KE∝t4
Thus, the kinetic energy acquired by the mass m is directly proportional to t4.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The velocity acquired by a mass m in travelling a certain distance d starting from rest under the action of a constant force is directly proportional to :-
View SolutionThe KE acquired by a mass m in travelling a certain distance s, starting from rest, under the action of a constant force is directly proportional to :
View Solution
Knowledge Check
The kinetic energy acquired by a mass m after travelling a fixed distance from rest under the action of constant force is
Adirectly proportional √mBinversely proportional to √mCdirectly proportional to m.Dindependent of m.A particle of mass 0.1 kg is subjected to a force which is directly proportional to the distance x. the work done by the force is directly proportional to
AxBx3Cx3/2Dx2
The K.E. acquired by a mass m in travelling a certain distance d, starting from rest, under the action of a constant force is directly propotional to
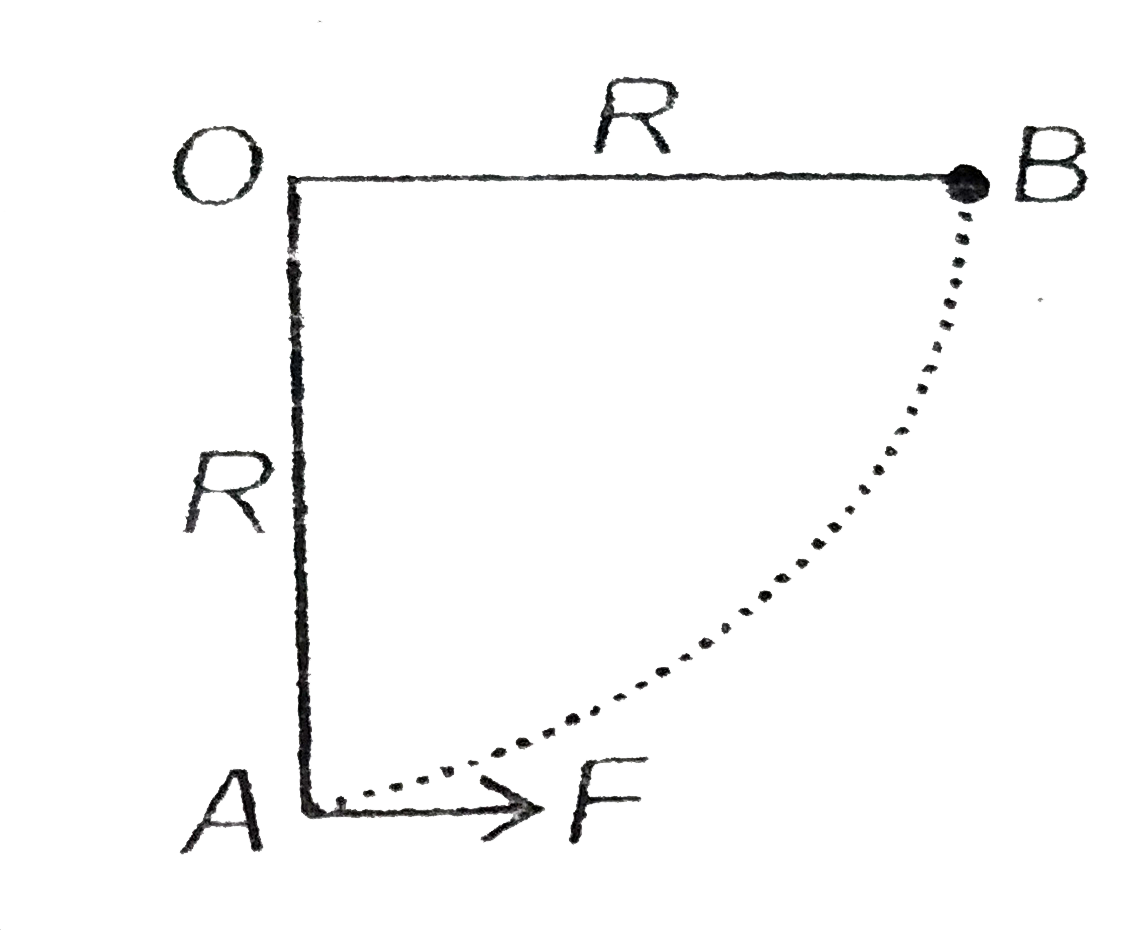
View SolutionA block of mass m is taken from A to B under the action of a constant force F. Work done by this force is
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA constant force acts on a mass m at rest. Velocity acquired in travelling a fixed distance is directly proportional to :
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionAn object of mass m, initially at rest under the action of a constant force F attains a velocity v in time t. Then, the average power supplied to mass is
View Solution
