The last soldier of an long marching troops runs from the end to its front, and then it runs back to the end with the same speed. During this, the marching troop covers a distance of . The distance covered by the soldier is
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the last soldier and the marching troop.
Step 1: Understand the scenario
The last soldier runs from the end of the troop to the front and then back to the end. The troop covers a distance of 150 meters during this time. The length of the troop is 80 meters.
Step 2: Define variables
Let:
- V1 = speed of the last soldier
- V2 = speed of the marching troop
- t = total time taken for the soldier to run to the front and back to the end
Step 3: Calculate the time taken by the troop
The marching troop covers a distance of 150 meters, so the time taken by the troop can be expressed as:
t=150V2
Step 4: Analyze the soldier's journey
1. First leg (running to the front): The soldier runs 80 meters towards the front. The effective speed of the soldier relative to the troop is V1−V2. The time taken for this leg is:
t1=80V1−V2
2. Second leg (running back to the end): The soldier runs back 80 meters to the end. The effective speed of the soldier relative to the troop is V1+V2. The time taken for this leg is:
t2=80V1+V2
Step 5: Relate the total time
The total time taken by the soldier is the sum of the times for both legs:
t=t1+t2=80V1−V2+80V1+V2
Step 6: Substitute the expression for t
We can substitute t from the troop's distance equation:
150V2=80V1−V2+80V1+V2
Step 7: Solve the equation
To solve this equation, we can cross-multiply and simplify:
1. Multiply both sides by V2(V1−V2)(V1+V2) to eliminate the denominators.
2. After simplification, we can find a relationship between V1 and V2.
Step 8: Calculate the distance covered by the soldier
The distance covered by the soldier is given by:
Distance=V1×t
Substituting t from the earlier expression, we can find the distance covered by the soldier.
Final Calculation
After solving the equations, we find that the distance covered by the soldier is:
Distance=250 meters
The last soldier runs from the end of the troop to the front and then back to the end. The troop covers a distance of 150 meters during this time. The length of the troop is 80 meters.
Let:
- V1 = speed of the last soldier
- V2 = speed of the marching troop
- t = total time taken for the soldier to run to the front and back to the end
The marching troop covers a distance of 150 meters, so the time taken by the troop can be expressed as:
t=150V2
1. First leg (running to the front): The soldier runs 80 meters towards the front. The effective speed of the soldier relative to the troop is V1−V2. The time taken for this leg is:
t1=80V1−V2
t2=80V1+V2
The total time taken by the soldier is the sum of the times for both legs:
t=t1+t2=80V1−V2+80V1+V2
We can substitute t from the troop's distance equation:
150V2=80V1−V2+80V1+V2
To solve this equation, we can cross-multiply and simplify:
1. Multiply both sides by V2(V1−V2)(V1+V2) to eliminate the denominators.
2. After simplification, we can find a relationship between V1 and V2.
The distance covered by the soldier is given by:
Distance=V1×t
Substituting t from the earlier expression, we can find the distance covered by the soldier.
After solving the equations, we find that the distance covered by the soldier is:
Distance=250 meters
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A uniform wooden plank of mass 150 kg and length 8 m is floating on still water with a man of 50 kg at one end of it . The man walks to the other end of the plank and stops. Than the distance covered by the plank is
View SolutionA body when projected vertically up from ground clovers a total distance D during the time of its flight t. If there were no gravity. The distance covered by it during the same time is equal to
View SolutionA man of mass m is standing at one end of a trolley of mass Mand length L placed at rest on a smooth horizontal surface. The man starts moving towards the other end and covers distance L, then distance moved by man w.r.t ground is
View SolutionShikha runs around a square of side 75m. Priya runs around a rectangle with length 60m and breadth 45m. Who covers the smaller distance?
View SolutionMoving with a uniform acceleration from the state of rest a body covers 22 m during the 6th sec of its motion. What is the distance covered by if during the first 6 sec?
View SolutionUsha swims in a 90m long pool. She covers 180m in one minute by swimming from one end to the other and back along the same length path. Find the average speed and average velocity of Usha.
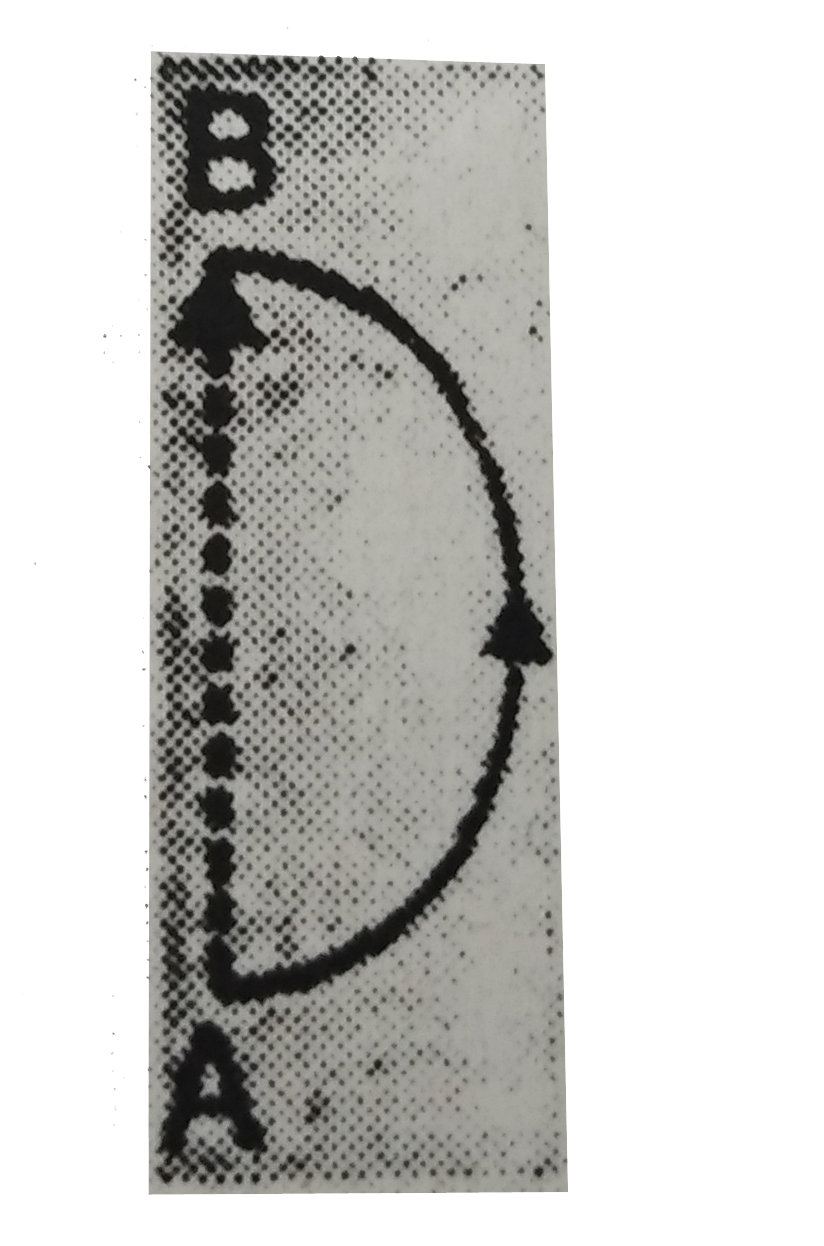
View SolutionA person moves on a semicircular track of radius 40 m. If he starts at one end of the track and reaches the other end, find the distance covered and magnitude of displacement of the person.
View SolutionAs shown in the figure, a bob of mass m is tied by a massless string whose other end is wound on a fly wheel Ring of radius r and mass m. When released from rest the bob starts falling vertically. When it has covered a distance of h, the speed of the bob will be :
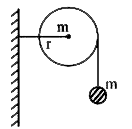
View SolutionAs shown in the figure, a bob of mass m is tied by a massless string whose other end is wound on a fly wheel Ring of radius r and mass m. When released from rest the bob starts falling vertically. When it has covered a distance of h, the speed of the bob will be :
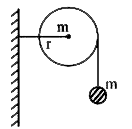
View SolutionA stone is dropped from the top of a tower of height 125 m. The distance travelled by it during last second of its fall is (g=10ms−2)
View Solution
