The length of a simple pendulum is 0.79m and the mass of the particle (the ''bob'') at the end of the cable is 0.24kg. The pendulum is pulled away from its equilibrium position by an angle of 8.50∘ and released from rest. Assume that friction can be neglected and that the resulting oscillatory motion is simple harmonic motion. What is the angular frequency of the motion?
9.1 rad/s
12 rad/s
8.2 rad/s
3.5 rad/s
The correct Answer is:D
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems39videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)4videos
PHOTONS AND MATTER WAVES
Similar Questions
The bob of pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. Find the speed v with which the bob passes through the equilibrium position.
View SolutionThe bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals
View Solution
Knowledge Check
- Question 1 - Select One
The bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
A√2g1−sinθB√2g1+cosθC√2g1−cosθD√2g1+sinθ - Question 2 - Select One
The bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
A√2g1−sinθB√2g1+cosθC√2g1−cosθD√2g1+sinθ - Question 3 - Select One
A simple pendulum consists of a ball of mass m suspended from the ceiling using a string of length L. The ball is displaced from its equilibrium position by a small angle θ. What is the magnitude of the restoring force that moves the toward its equilibrium position and produces simple harmonic motion?
AkxBmgCmg(cosθ)Dmg(sinθ)
The bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
View SolutionA pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
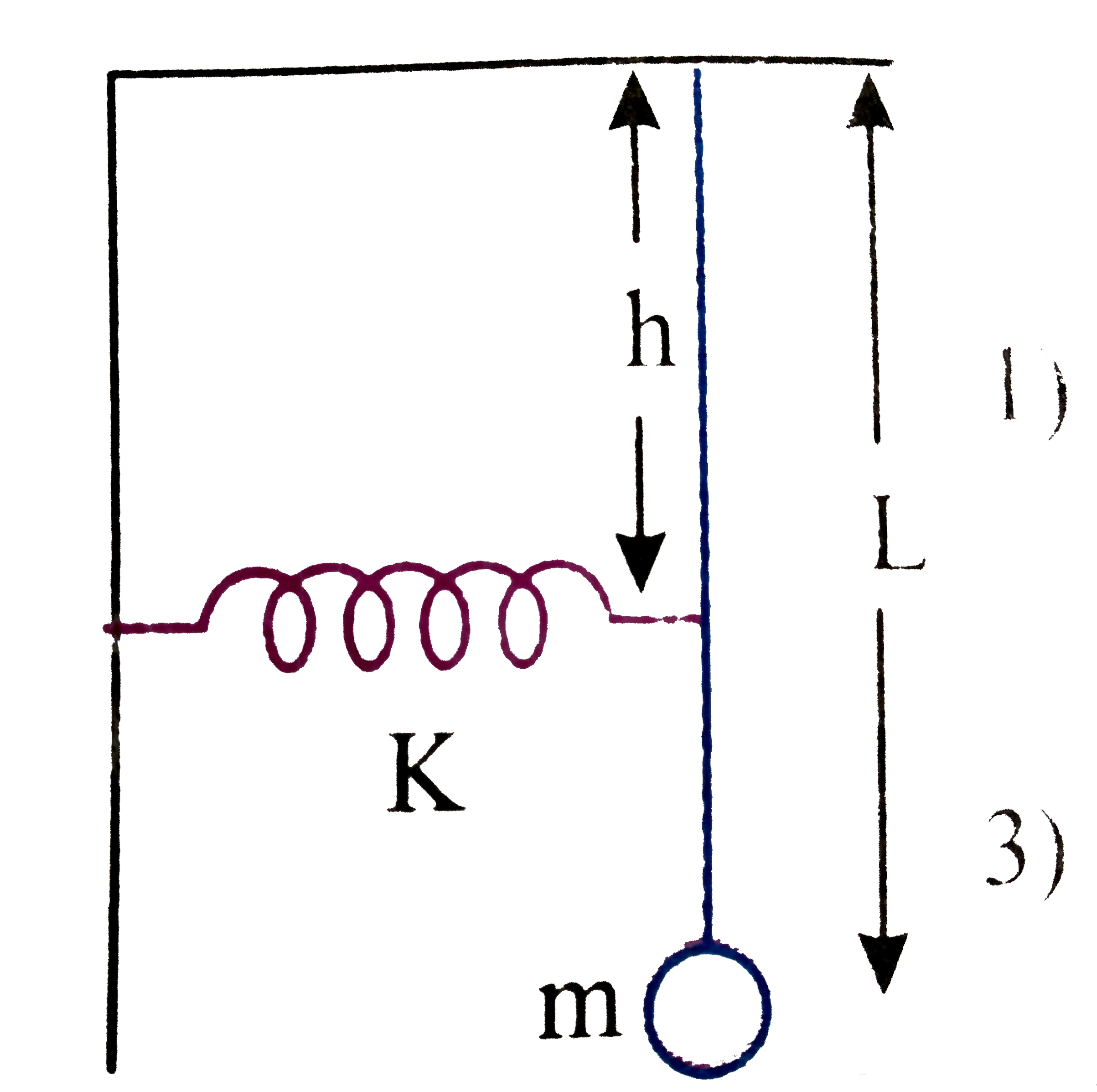 View Solution
View SolutionThe bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals
View SolutionThe mass of a simple pendulum bob is 100 gm. The length of the pendulum is 1 m. The bob is drawn aside from the equilibrium position so that the string makes an angle of 60∘ with the vertical and let go. The kinetic energy of the bob while crossing its equilibrium position will be
View SolutionThe bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
View Solution

