A simple pendulum consists of a ball of mass m suspended from the ceiling using a string of length L. The ball is displaced from its equilibrium position by a small angle θ. What is the magnitude of the restoring force that moves the toward its equilibrium position and produces simple harmonic motion?
kx
mg
mg(cosθ)
mg(sinθ)
The correct Answer is:D
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems
39 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
A particle of mass m is suspended from a fixed point O by a string length l.At t=0, it is displaced from its equilibrium position and released.If T is the tension in the string with time t, then the correct graph is
View SolutionA simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
View Solution
Knowledge Check
A particle of mass m is suspended from a fixed O by a string of length L. At t=0, it is displaced from its equilibrium position and released. The graph which shows the variation of the tension T in the string with time t is :
 A
A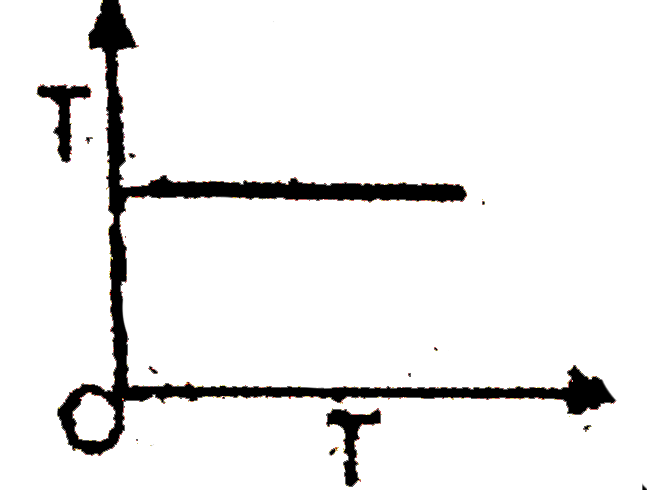 B
B C
C D
D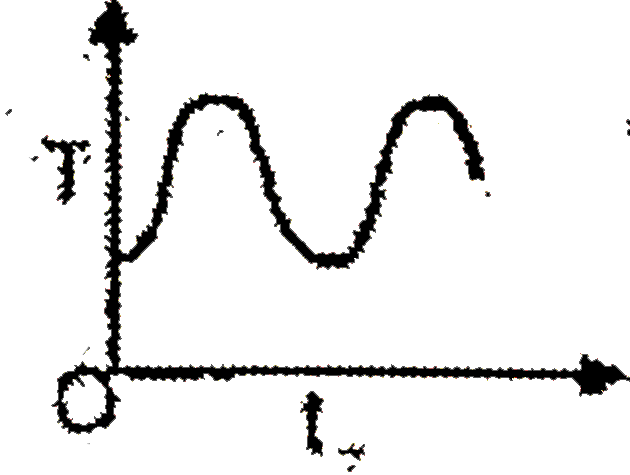
The bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
A√2g1−sinθB√2g1+cosθC√2g1−cosθD√2g1+sinθThe bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
A√2g1−sinθB√2g1+cosθC√2g1−cosθD√2g1+sinθ
The bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals
View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
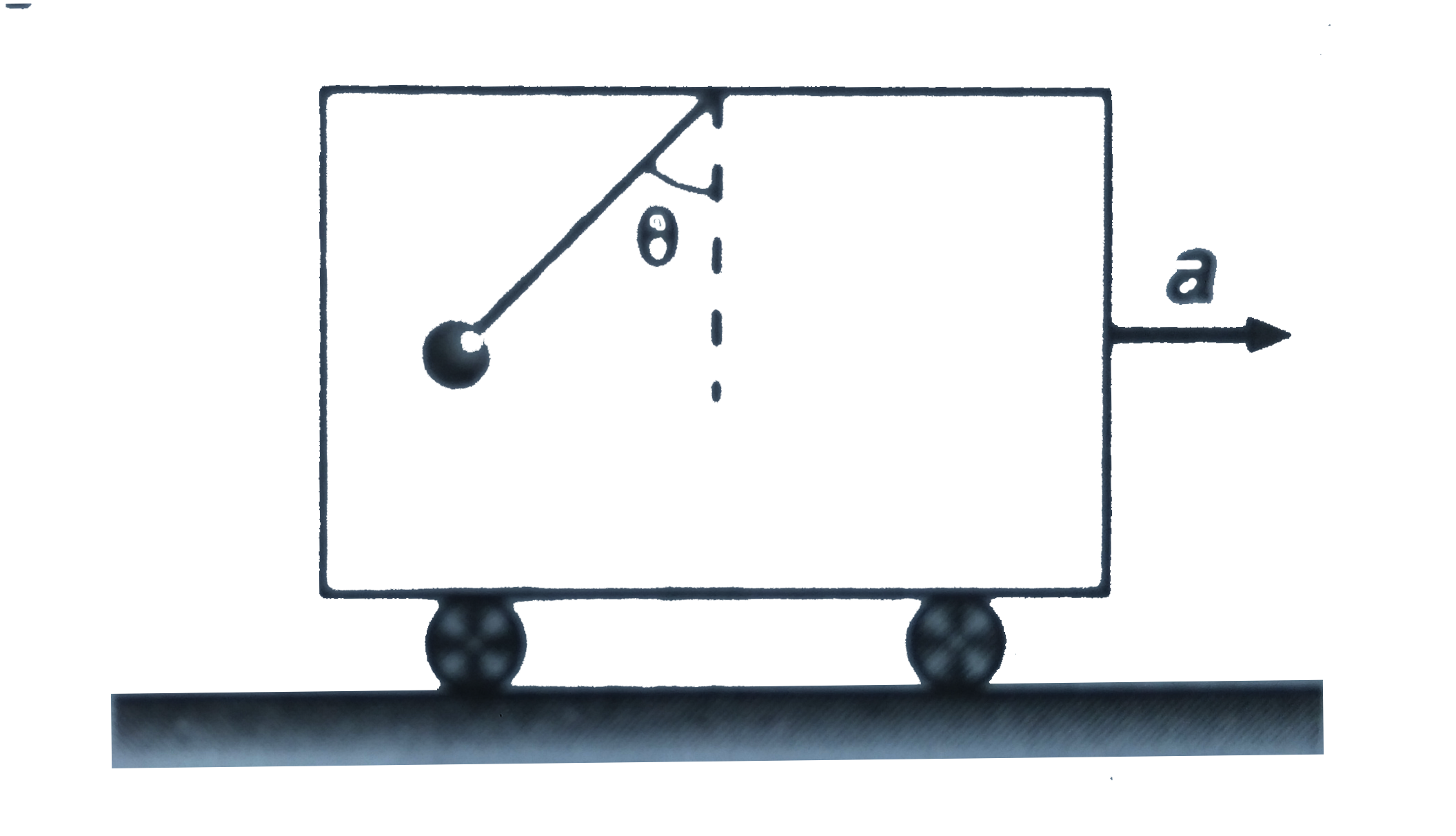
View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.

View SolutionA pendulum is displaced to an angle θ from its equilibrium position, then it will pass through its mean position with a velocity v equal to
View SolutionA pendulum is displaced to an angle θ from its equilibrium position, then it will pass through its mean position with a velocity v equal to
View Solution
