The length of an iron wire is L and area of cross-section is A. The increase in length is l on applying the force F on its two ends. Which of the statement is correct
increase in length is inversely proportional to its length L
Increase in length is proportional to area of cross-section A
Increase in length is inversely proportional to A
Increase in length is proportional to Young's modulus
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the elongation of the wire and the parameters given: the original length (L), the area of cross-section (A), the applied force (F), and Young's modulus (Y).
1. Understanding the Concept:
The elongation (increase in length) of a wire when a force is applied is described by Hooke's Law, which states that the elongation is directly proportional to the force applied and the original length of the wire, and inversely proportional to the area of cross-section and Young's modulus of the material.
2. Using the Formula:
The formula for elongation (ΔL) can be expressed as:
ΔL=F⋅LA⋅Y
where:
- ΔL = increase in length (elongation)
- F = applied force
- L = original length of the wire
- A = area of cross-section
- Y = Young's modulus of the material
3. Analyzing the Relationship:
From the formula, we can see that:
- ΔL is directly proportional to F and L.
- ΔL is inversely proportional to A and Y.
4. Identifying the Correct Statement:
Since the question asks which statement is correct regarding the increase in length (ΔL), we can conclude:
- As the area of cross-section A increases, the elongation ΔL decreases, indicating that the increase in length is inversely proportional to the area of cross-section.
5. Conclusion:
Therefore, the correct statement is that the increase in the length (ΔL) is inversely proportional to the area of cross-section (A).
Final Answer:
The increase in the length is inversely proportional to the area of cross-section (A).
---
The elongation (increase in length) of a wire when a force is applied is described by Hooke's Law, which states that the elongation is directly proportional to the force applied and the original length of the wire, and inversely proportional to the area of cross-section and Young's modulus of the material.
The formula for elongation (ΔL) can be expressed as:
ΔL=F⋅LA⋅Y
where:
- ΔL = increase in length (elongation)
- F = applied force
- L = original length of the wire
- A = area of cross-section
- Y = Young's modulus of the material
From the formula, we can see that:
- ΔL is directly proportional to F and L.
- ΔL is inversely proportional to A and Y.
Since the question asks which statement is correct regarding the increase in length (ΔL), we can conclude:
- As the area of cross-section A increases, the elongation ΔL decreases, indicating that the increase in length is inversely proportional to the area of cross-section.
Therefore, the correct statement is that the increase in the length (ΔL) is inversely proportional to the area of cross-section (A).
The increase in the length is inversely proportional to the area of cross-section (A).
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Match the columns
4 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.3
15 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
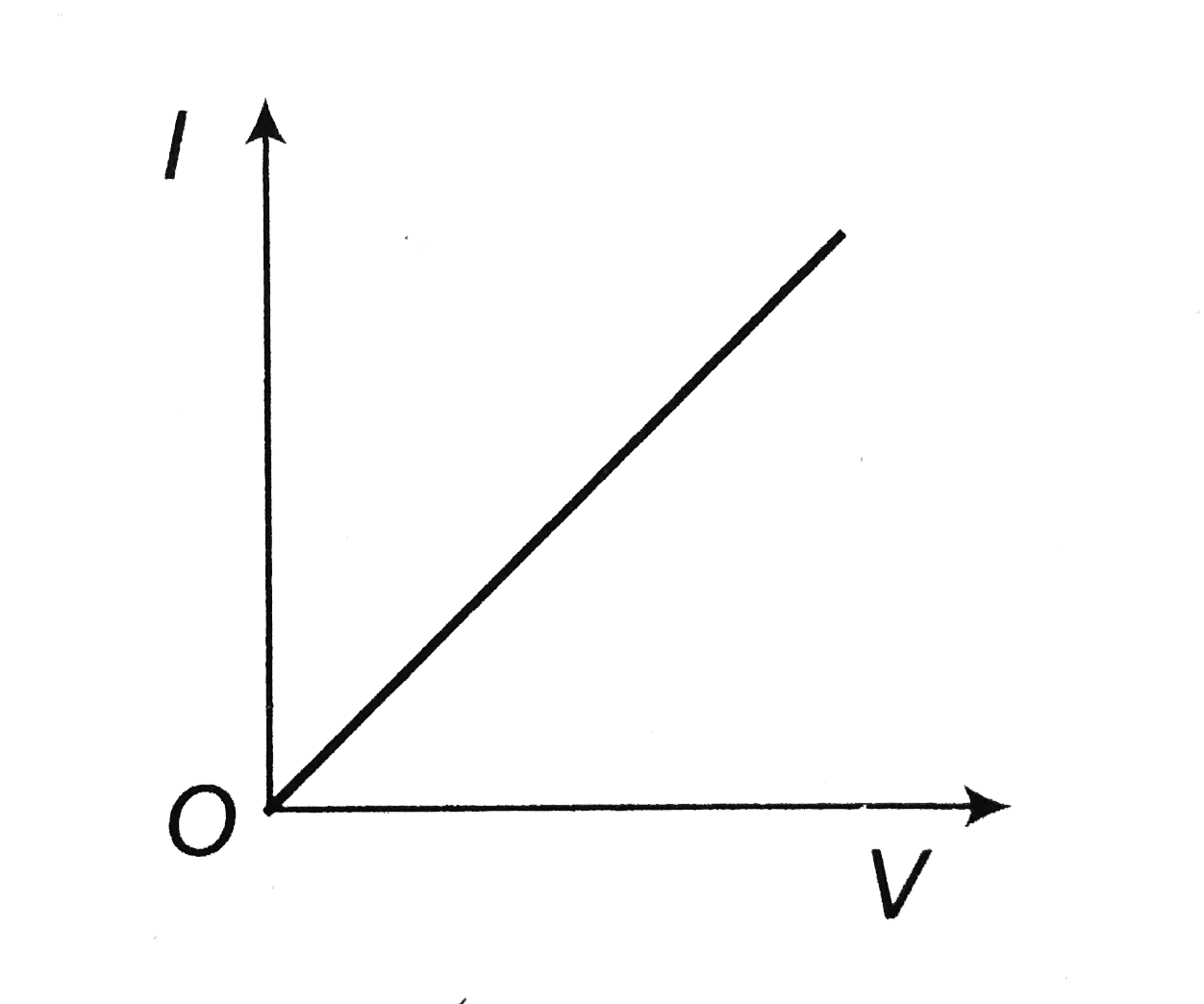
I−V characterstic of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
View SolutionThe self inductance of a solenoid of length L, area of cross-section A and having N turns is-
View SolutionThe magnetic energy stored in a long solenoid of area of cross-section A in a small region of length L is
View Solution
The pressures at A and B in the atmosphere are, respectively,
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionConsider a wire of length l, area of cross section A, and resistivity ρ with resistance 10Ω. Its length is increased by applying a force, and it becomes four times of its original value. Find the changed resistance of the wire.
View SolutionConsider a wire of length l , area of cross-section A and resistivity ρ and resistance 15Ω. Its length is increased by applying a force on I and its length increases by four times of its original length. Find the new resistance in ohms of the wire.
View SolutionWhen a steel wire fixed at one end is pulled by a constant force F at its other end , its length increases by l.Which of the following statements is not correct?
View SolutionTwo wires are made of the same material and have the same volume. However wire 1 has cross-sectional area A and wire 2 has cross-sectional area 3A. If the length of wire 1 increases by Δx on applying force F, how much force is needed to stretch wire 2 by the same amount?
View Solution
