The length of the wire shown in figure between the pulley is 1.5 m and its mass is 12.0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.

Tension in wire
T=9kgwt=9g=9×9.8
Mass per unit length mM/L
=12×10−3kg1.5m=8×10−3kg/m
∴ Frequency of vibration of pth harmonic on string
n=p2l√Tm=22×1.5√{9×9.88×10−3}=70Hz
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The length of the wire shown in figure between the pulleys is 1.5 m and its mass is 15 g. what is the frequency of vibration with which the wire vibrates in four loops leaving the middle point of the wire between the pullys at rest ? (g=10ms2)
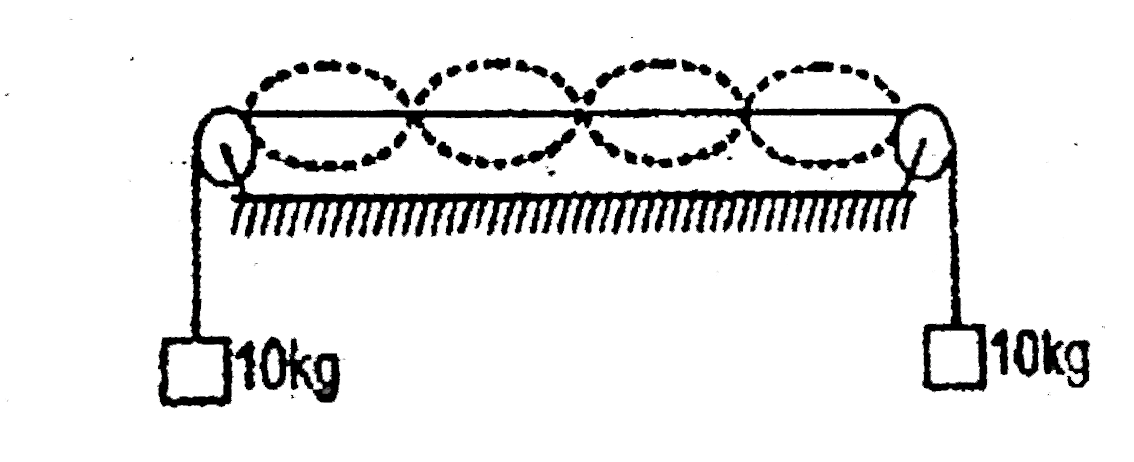
View SolutionThe length of a sonometer wire tuned to a frequency of 256 Hz is 0.6 m. Calculate the frequency of the tuning fork with which the vibrating wire will be in tune when the length is made 0.4 m
View SolutionThe length of a sonometer wire tuned to a frequency of 250 Hz is 0.60 metre . The frequency of tuning fork with which the vibrating wire will be in tune when the length is made 0.40 metre is
View SolutionThe length of a stretched wire is 1 m and its fundamental frequency is 300 Hz.What is the speed of the transverse wave in the wire ?
View SolutionAn aluminium wire of cross-sectional area (10−6)m2 is joined to a steel wire of the same cross-sectional area. This compound wire is stretched on a sonometer pulled by a weight of 10kg. The total length of the compound wire between the bridges is 1.5m of which the aluminium wire is 0.6m and the rest is steel wire. Transverse vibrations are setup in the wire by using an external source of variable frequency. Find the lowest frequency of excitation for which the standing waves are formed such that the joint in the wire is a node. What is the total number of nodes at this frequency? The density of aluminium is 2.6×(103)kg/m3 and that of steel is 1.04×104kg/m2(g=10m/s2)
View SolutionIf the wire is gently tapped in vertical direction halfway between the pulleys, what is the lowest frequency at which it will vibrate transversely? The mass per unit length of the eire is 0.02 kg/m and it has a length of0.2 m between pulleys. Volume of block is 1200m3and its mass is 10kg.
_PHY_E06_340_Q01.png)
View SolutionTwo wires are together end to end . The wires are made of the same material , but the diameter of one is twice that of the other . They are subjected to a tension of 4.60N. The thin wire has a length of 40.0cm and a linear mass density of 2.00g/m. The combination is fixed at both ends and vibrated in such a way that two antinodes are present , with the node between them being precisely at the weld . (a) What is the frequency of vibration ? (b) Find the length of the thick wire .
View SolutionA tube 1.0m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3m long and a mass of 0.01kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = 330m/s .
View SolutionThe total length of a sonometer wire fixed between two bridges is 110 cm. Now, two more bridges are placed to divide the length of the wire in the ratio 6:3:2. If the tension in the wire is 400 N and the mass per unit length of the wire is 0.01 kg m−1, then the minimum common frequency with which all the three parts can vibrate, is
View SolutionA uniform wire of length I and mass M is stretched between two fixed points, keeping a tension F. A sound of frequency μ is impressed on it. Then the maximum vibrational energy is existing in the wire when μ
View Solution
