The magnetic field existing in a region is given by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
(a) v0B0d2a
(b) v0B0d3a2
( c) v0B0d
(d) zero
The correct Answer is:A
(a) Magnetic field at sid e(1): B1=B0
induced emf in (1): e1=B0v0d

Magnetic field at side (2): (B2=B0[1+da]
Induced emf in 3and4will be zero.
Net emf: e=e2−e1=B0v0d2a
Alternate mathod:
Let at any instant, the loop is at distance y as shown below.
Let us take anticlockwise direction to be positive.

flux through a strip of width dx: dϕ=B0[1+xa](d)(dx)
Net flux: ϕ=B0d∫y+dy(1+xa)
→ ϕ=B0d[x+x22a]y+dy
→ ϕ=B0d[d+12a[(y+d)2−y2]]
→ ϕ=B0d[d+12−d(2y+d)]
e=−dϕdt=−B−(0)d[12a−d(2y+d)]
→ e=−B0d2adydt=−B0d2av0
Negative sign indicates that emf induced is clockwise.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
The magnetic field existing in a region is given by ,B=B0(xL+x2L2)ˆk.A square loop edge L carrying a current I is placed with its parallel to the X and Y-axis Find the net magnetic force experienced by the loop
View SolutionThe magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
View SolutionA hypthetical magnetic field existing in a region is given by →B=B0→er, where →–––r denotes the uit vector along the redial direction. A circular loop of radus a, carrying a current I, is placed with its plane parallel to the x-y plane and the centre at (0,0, d) .Find the magnitude of the magnetic force acting on the loop.
View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.
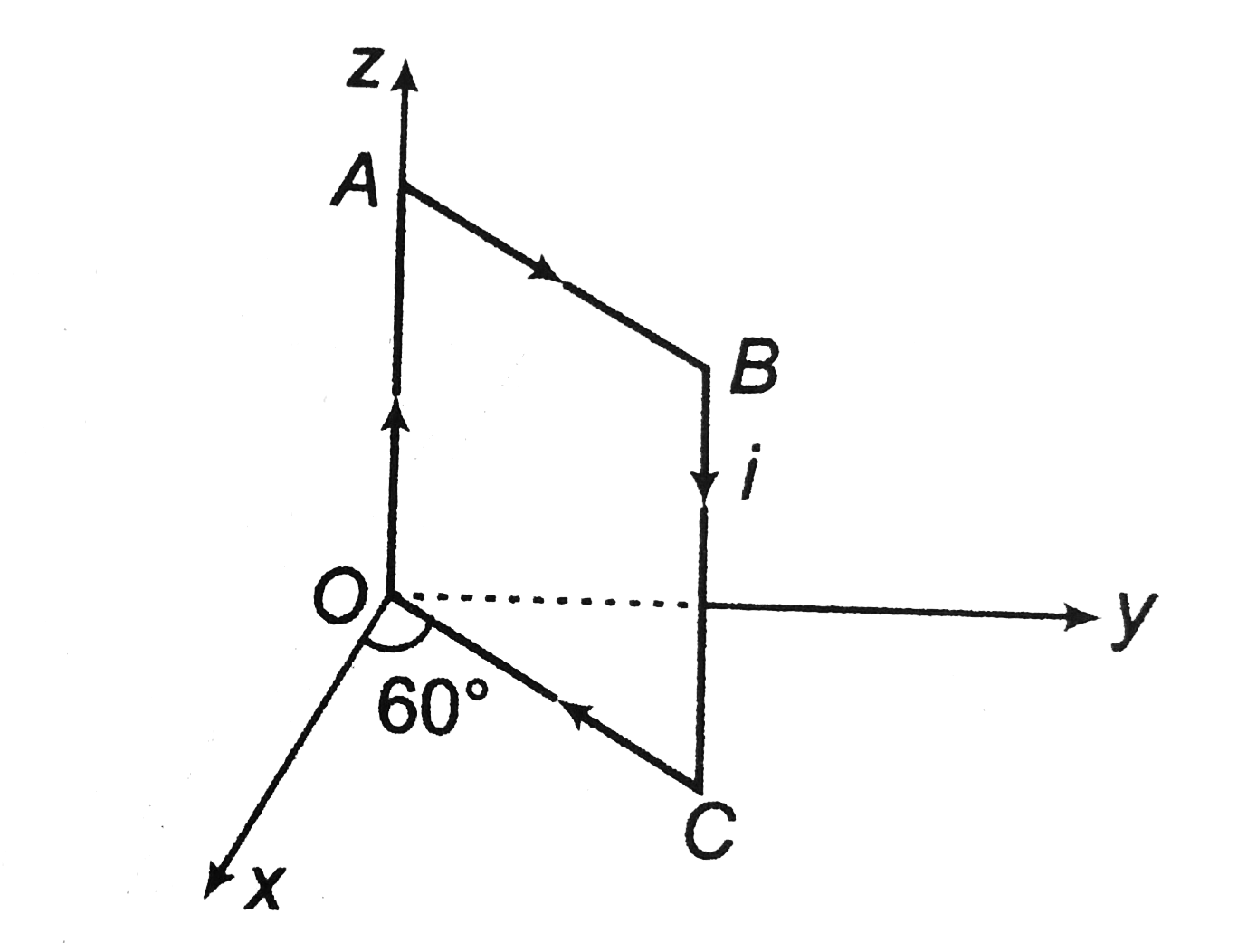
View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionA wire carrying current i is bent as shown in figure and placed in the plane of uniform magnetic field Bvec. The magnitude of magnetic force experienced by
View SolutionThe magnetic field I nan reigion is given by B=B0XaK. A Squrae edges along the x and y axis. The loop is moved with a constant velocity . The emf induced in the loop is

View SolutionA wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
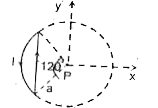
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
View SolutionA triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View Solution
