The magnetic flux through a coil is varying according to the relation ϕ=(5t3+4t2+2t−5) Wb. Calculate the induced current through the coil at t=2 s if resistiance of coil is 5 ohm.
To solve the problem, we need to follow these steps:
Step 1: Find the expression for induced EMF
The induced electromotive force (EMF) in a coil is given by Faraday's law of electromagnetic induction, which states that the induced EMF (ε) is equal to the negative rate of change of magnetic flux (φ) through the coil:
ε=−dϕdt
Step 2: Differentiate the magnetic flux function
Given the magnetic flux function:
ϕ(t)=5t3+4t2+2t−5
We need to differentiate this with respect to time (t):
dϕdt=ddt(5t3+4t2+2t−5)
Using the power rule of differentiation:
dϕdt=15t2+8t+2
Step 3: Substitute t = 2 seconds into the derivative
Now we substitute t=2 seconds into the differentiated expression:
dϕdt∣∣∣t=2=15(22)+8(2)+2
Calculating this step-by-step:
=15(4)+16+2
=60+16+2
=78
Step 4: Calculate the induced EMF
Now, we can find the induced EMF:
ε=−dϕdt=−78V
Step 5: Calculate the induced current using Ohm's law
Using Ohm's law, the induced current (I) can be calculated as:
I=εR
Where R is the resistance of the coil, which is given as 5 ohms:
I=−785
Calculating the current:
I=−15.6A
The negative sign indicates that the direction of the induced current is opposite to the assumed direction.
Final Answer
The induced current through the coil at t=2 seconds is 15.6A (in the opposite direction).
---
The induced electromotive force (EMF) in a coil is given by Faraday's law of electromagnetic induction, which states that the induced EMF (ε) is equal to the negative rate of change of magnetic flux (φ) through the coil:
Given the magnetic flux function:
Now we substitute t=2 seconds into the differentiated expression:
=60+16+2
=78
Now, we can find the induced EMF:
Using Ohm's law, the induced current (I) can be calculated as:
The induced current through the coil at t=2 seconds is 15.6A (in the opposite direction).
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
The magnetic flux through a coil varies with time t as follows:
ϕt=(8t3−6t2+t−5)Wb
What is the induced current through the coil at t = 4 s, given that the resistance of the coil is 10 Ω and the magnetic flux through the coil is perpendicular to its plane?View SolutionThe magnetic flux through a loop is varying according to relation ϕ=6t2+7t+1 where ϕ is in milliweber and t is in second. What is the e.m.f. induced in the loop at t = 2 second ?
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(2t2+4t+6)mWb. The emf induced in the loop at t=4 s is
A0.12 VB2.4 VC0.02 VD1.2 V - Question 2 - Select One
The magnetic flux through a coil varies with time as ϕ=5t2+6t+9 The ratio of emf at t = 3 s to t = 0 s will be
A9:1B1:6C6:1D1:9 - Question 3 - Select One
The magnetic flux linked with a coil is given by an equation ϕ=5t2+2t+3.
The induced e.m.f. in the coil at the third second will beA32 unitsB54 unitsC40 unitsD65 units
The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(5t2+10t+5) milliweber. Calculate the e.m.f. induced in the loop at t=5 s.
View SolutionThe magnetic flux (in weber) linked with a coil of resistance 10Ω is varying with respect to time t ϕ=4t2+2t+1. Then the current in the coil at time t = 1 second is
View SolutionIn the given figure the magnetic flux through the loop increases according to the relation
ϕB(t)=10t2+20t, where ϕB is in milliwebers and t is in seconds.
The magnitude of current throught R=2Ω resistor at t=5 s is _______ mA.
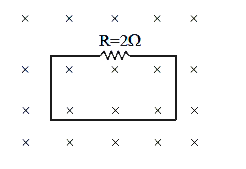 View Solution
View SolutionThe magnetic flux through a loop is varying according to relation ϕ=6t2+7t+1 where ϕ is in milliweber and t is in second. What is the e.m.f. induced in the loop at t = 2 second ?
View SolutionThe magnetic flux through a coil varies with time as ϕ=5t−6t+9. The ratio of E.M.F. at t=0s to t=0.5s will be
View Solution

