The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(5t2+10t+5) milliweber. Calculate the e.m.f. induced in the loop at t = 2s, if the resistance of the coil is 5 ohm.Solution in Punjabi
Step by step video & image solution for The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation phi = (5 t^(2) + 10 t + 5) milliweber. Calculate the e.m.f. induced in the loop at t = 2s, if the resistance of the coil is 5 ohm. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE146videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRICAL MEASUREMENTSEXERCISE - EXERCISE44videos
ELECTRICAL MEASUREMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE66videos
ELECTROMAGNETIC WAVES
Similar Questions
Explain the concept of magnetic flux linked with a surface.
03:13View SolutionState and explain Kirchhoff's laws.
02:33View SolutionWhy did Maxwell introduce the concept of displacement current ?Explain.
02:28View SolutionThe magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(5t2+10t+5) milliweber. Calculate the e.m.f. induced in the loop at t=5 s.
01:39View SolutionThe magnetic flux through a coil is varying according to the relation phi = (5 t^(3) + 4 t^(2) + 2t - 5) Wb. Calculate the induced current through the coil at t = 2 s if resistiance of coil is 5 ohm.
03:39View SolutionIn the figure the flux through the loop perpendicular to the plane of the coil and direciton into the paper varying according to the relation ϕ=6t2+7t+I where ϕ is in milliweber and t is in loop at t=2s and direction of induced current through R are
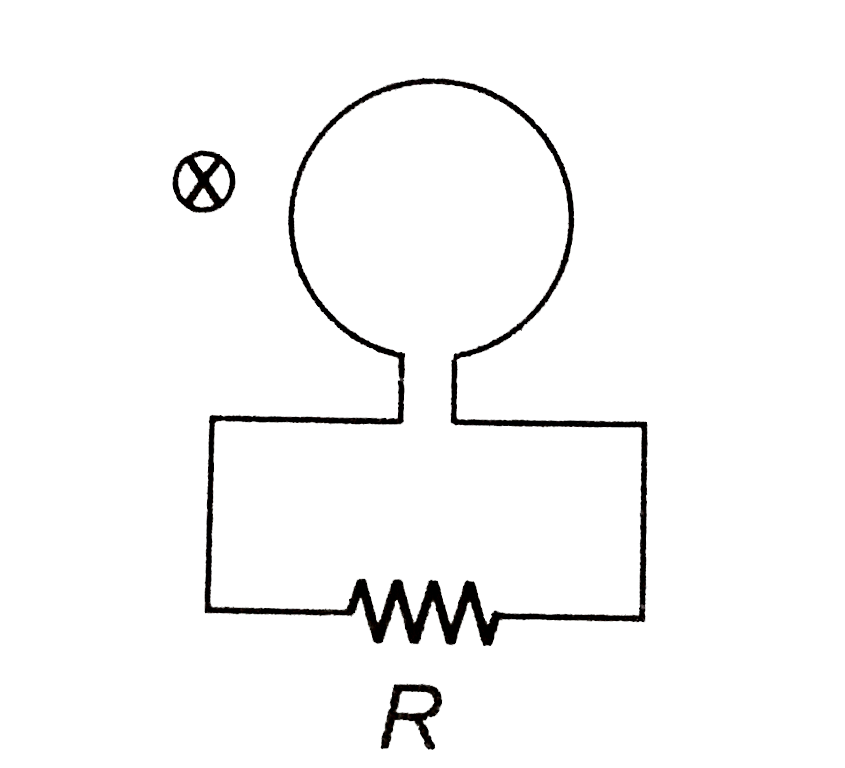 02:45View Solution
02:45View SolutionThe magnetic flux through a loop is varying according to relation ϕ=6t2+7t+1 where ϕ is in milliweber and t is in second. What is the e.m.f. induced in the loop at t = 2 second ?
02:02View SolutionThe magnetic flux through a coil is varying according to the relation phi=(4t^(2)+2t-5)Wb , t measured in seconds. Calculate the induced current through the coil at t = 2s, if the resistance of the coil is 5Omega .
02:19View SolutionThe magnetic flux phi through a coil is varying w.r.t. time 't' according to the relation phi=5t^(2)+4t+3 weber. Calculate the induced e.m.f. and current in the coil at t=3 sec. The resistance of the coil is 2Omega .
02:25View SolutionThe magnetic flux through a coil perpendicular to its plane and directed into the paper is varying according to the relation, ϕ=(3t3+2t2+4t+6) Wb. Calculate the e.m.f. induced in the coil at t = 2s.
02:20View SolutionThe magnetic flux through a coil perpendicular to its plane and directed into the paper is varying according to the relation, ϕ=(2t3−t2−3t+5) Wb. Calculate the e.m.f. induced in the coil at t = 2s.
02:03View SolutionThe magnetic flux through a coil perpendicular to its plane and directed into the paper is varying according to the equation phi = (2t^3 -6t^2-t + 8) Wb. Calculate the e.m.f. induced in the coil at t = 3s.
02:20View SolutionThe magnetic flux through a coil perpendicular to its plane and directed into paper varying according to the relation phi= (5t^2+10t+5) mWb. Calculate the emf induced at t= 5 sec.
View SolutionThe magnetic flux passing perpendicular to the plane of the coil and directed into the paper is varying according to the relation phi=6t^2 +7t+1 Where phi is in milliweber and t is in seconds. what is the magnitude of e.m.f. induced in the loop when t=2s?
View SolutionThe magnetic flux passing perpendicular to the plane of the coil and directed into the paper is varying according to the relation phi=6t^2 +7t+1 Where phi is in milliweber and t is in seconds. What is the direction of current through resistor R?
View SolutionThe magnetic flux through a coil is perpendicular to its plane and directed into the paper is verying according to the relation ϕ=(3t2+2t2+4t+6)wb. Find the e.m.f. induced in the coil at t = 1 s.
02:51View Solution

