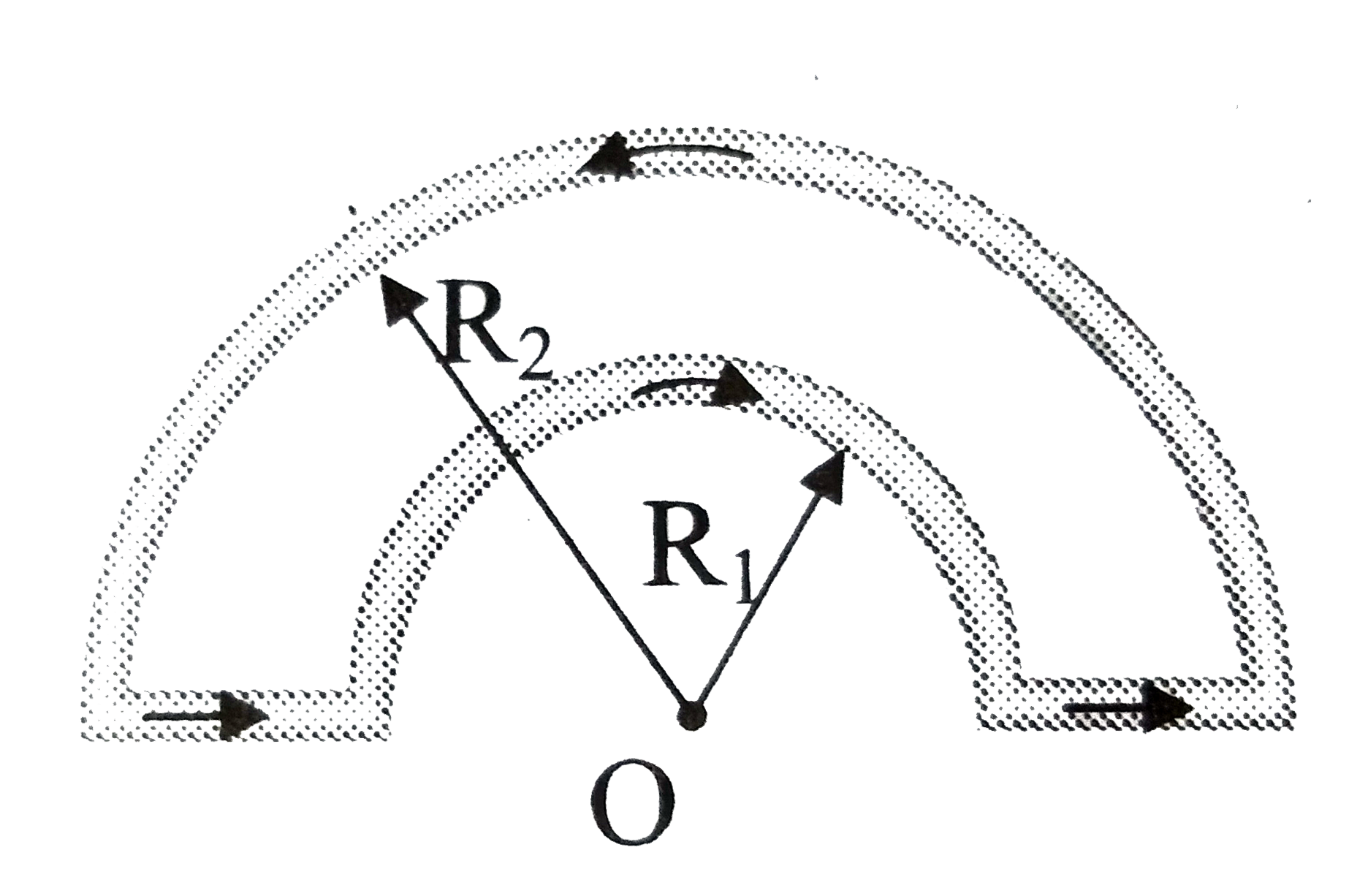
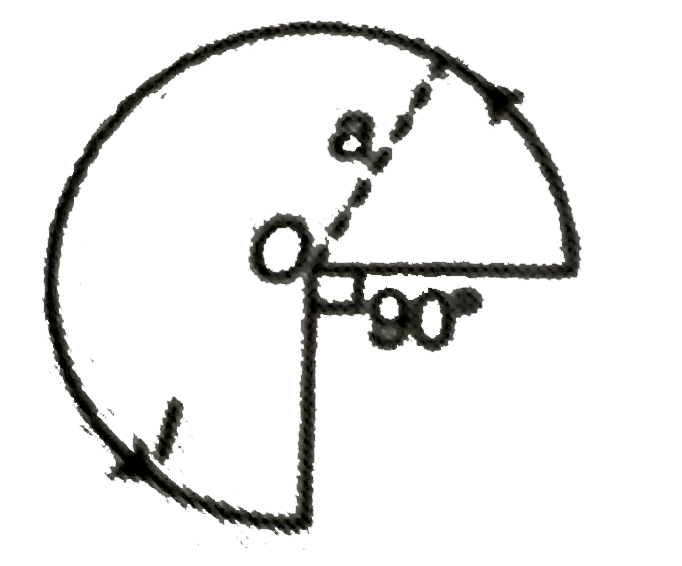
The magnetic induction at centre O Fig.

A

$\frac{μ_{0} I}{2 a} + \frac{μ_{0} I}{2 b} \otimes$

B

$\frac{3 μ_{0} I}{8 a} + \frac{μ_{0} I}{8 b} \otimes$

C

$\frac{3 μ_{0} I}{8 a} - \frac{μ_{0} I}{8 b} \otimes$

D

$\frac{3 μ_{0} I}{8 a} + \frac{μ_{0} I}{8 b} \otimes$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$B = \frac{3}{4} [\frac{μ_{0} I}{2 a}] + \frac{1}{4} [\frac{μ_{0} I}{2 b}]$
$B = \frac{3 μ_{0} I}{8 a} + \frac{μ_{0} I}{8 b}$

Updated on:21/07/2023

|

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

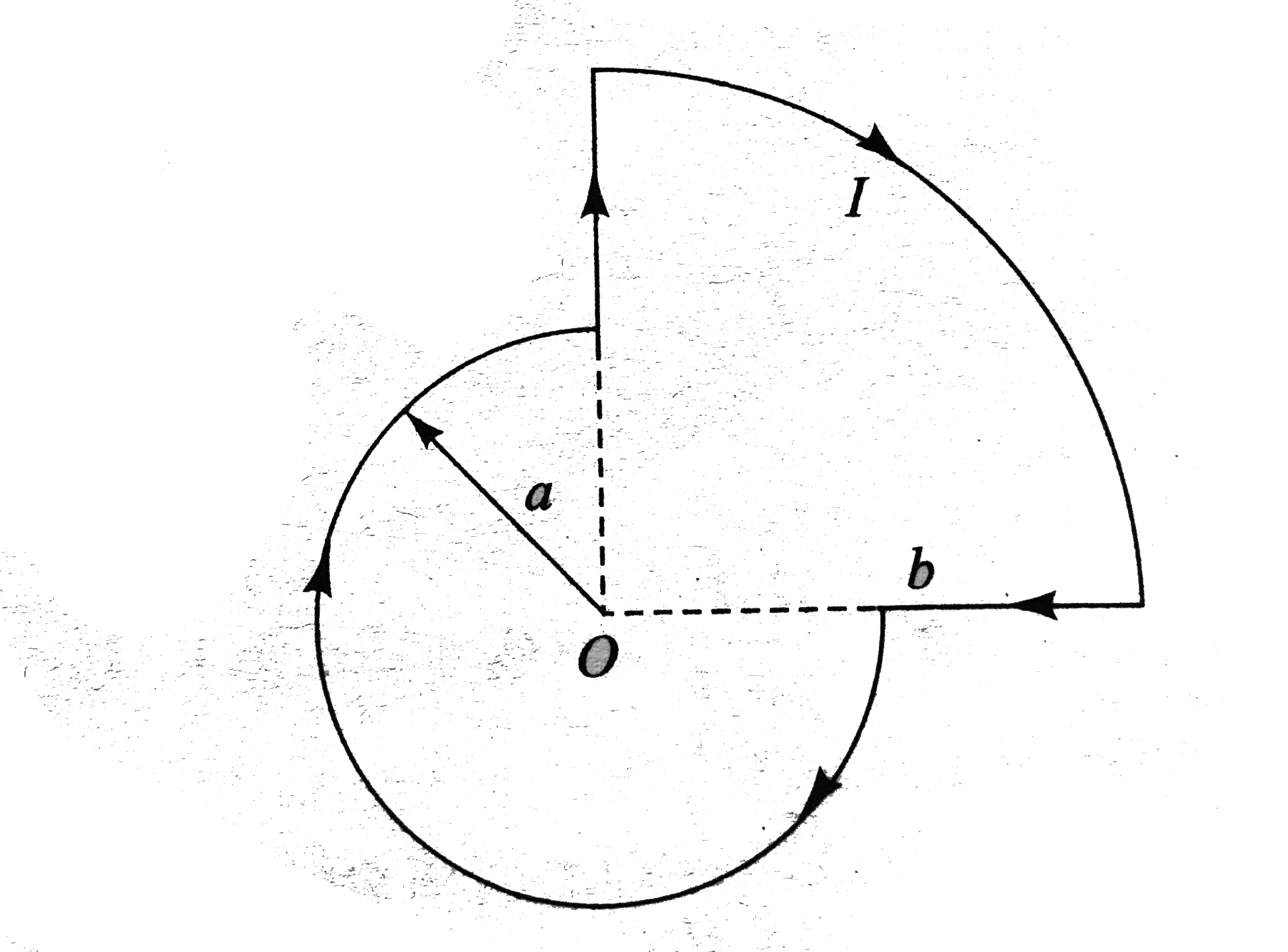
The magnetic induction at centre O in the following figure will be

A $\frac{μ_{0} i α}{4 π} (\frac{1}{r_{1}} - \frac{1}{r_{2}}) ⊙$
B $\frac{μ_{0} i α}{4 π} (\frac{1}{r_{1}} + \frac{1}{r_{2}}) ⊙$
C $\frac{μ_{0} i α}{2 π} [\frac{1}{r_{1}} - \frac{1}{r_{2}}] \otimes$
D $\frac{μ_{0} i α}{2 π} [\frac{1}{r_{1}} + \frac{1}{r_{2}}] \otimes$
The magnetic induction at the centre $O$ in the figure shown in

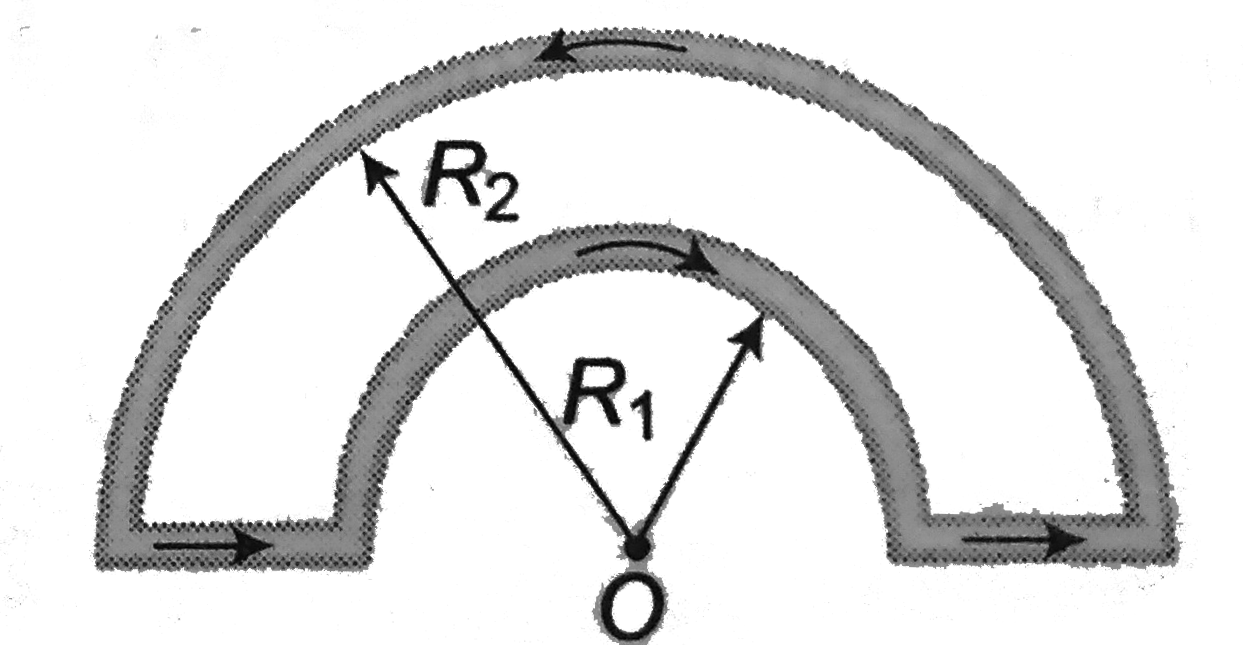A $\frac{μ_{0} i}{4} (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
B $\frac{μ_{0} i}{4} (R_{1} + R_{2})$
C $\frac{μ_{0} i}{4} (R_{1} + R_{2})$
D $\frac{μ_{0} i}{4} (R_{1} + R_{2})$
In the figure shown there are two semicircles of radii $r_{1}$ and $r_{2}$ in which a current $i$ is flowing. The magnetic induction at the centre $O$ will be

A $\frac{μ_{0} i}{r} (r_{1} + r_{2})$
B $\frac{μ_{0} i}{4} (r_{1} - r_{2})$
C $\frac{μ_{0} i}{4} (\frac{r_{1} + r_{2}}{r_{1} r_{2}})$
D $\frac{μ_{0} i}{4} (\frac{r_{1} - r_{2}}{r_{1} r_{2}})$

A2Z-SOURCE AND EFFECT OF MAGNETIC FIELD-Magnetic Field Due To Circular Arc

Home
Ask Doubt
Profile