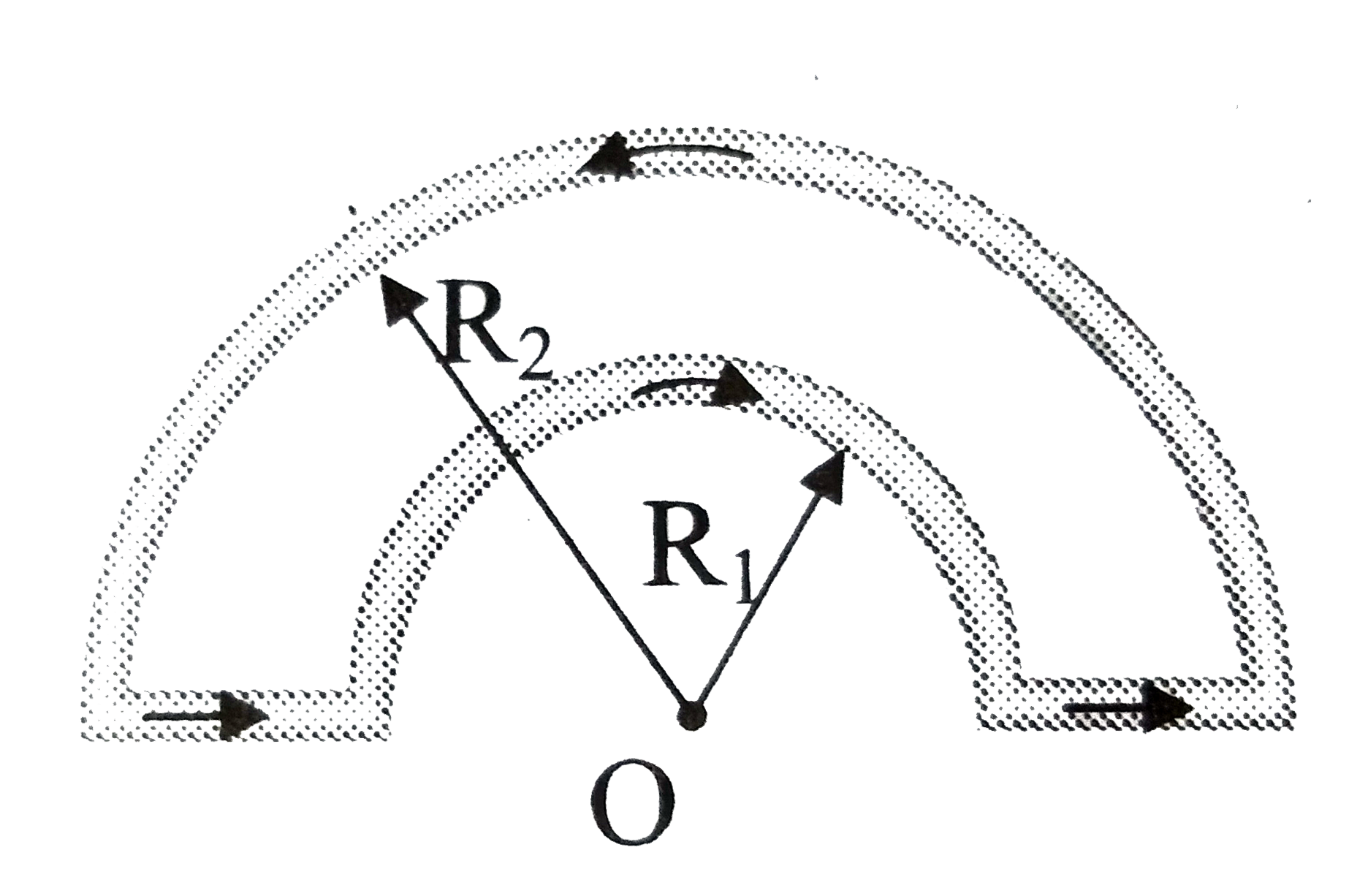
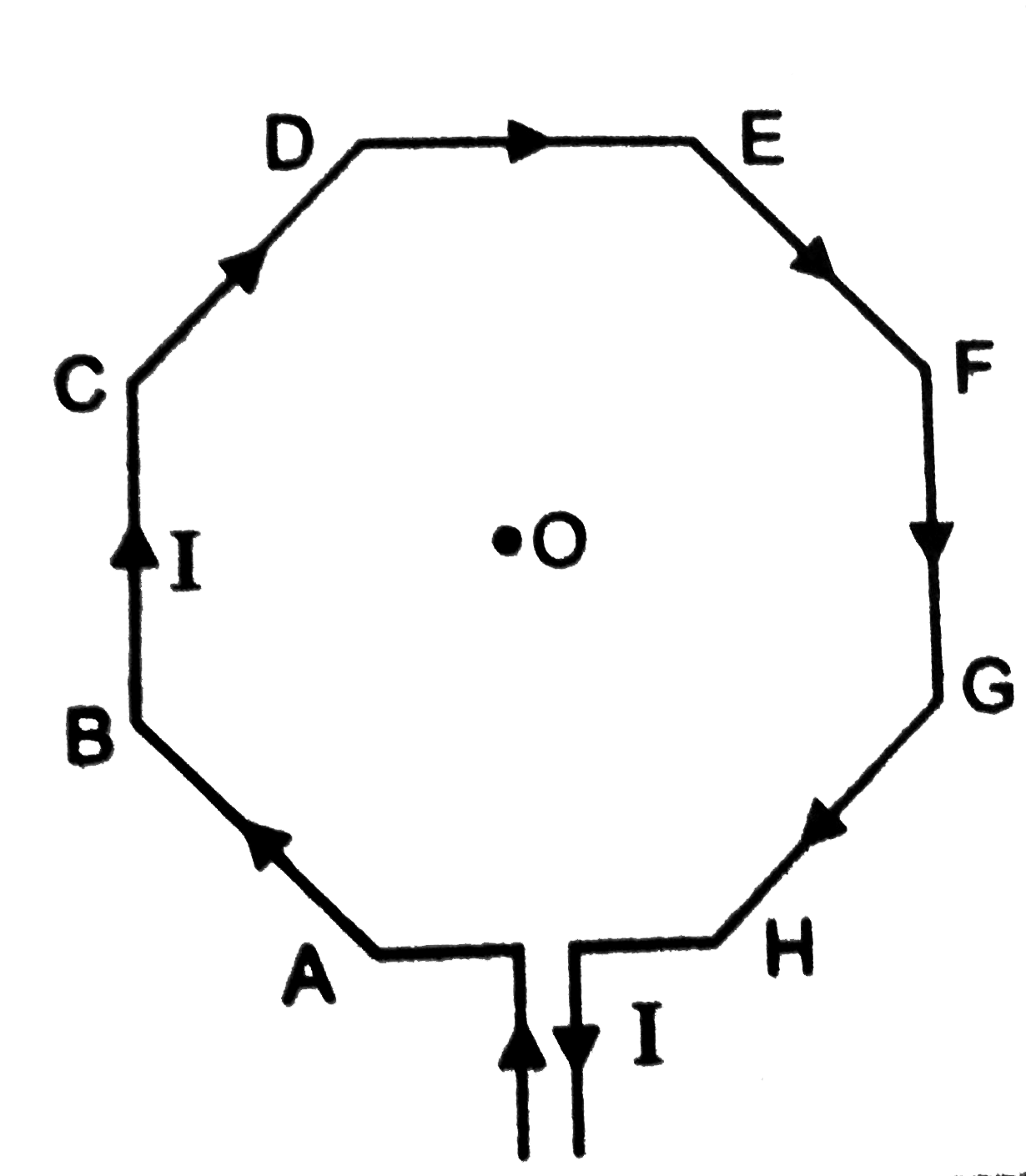
The magnetic induction at the centre O in the figure shown in
A
μ0i4(1R1−1R2)
B
μ0i4(R1+R2)
C
μ0i4(R1+R2)
D
μ0i4(R1+R2)
Video Solution
Text Solution
The correct Answer is:A
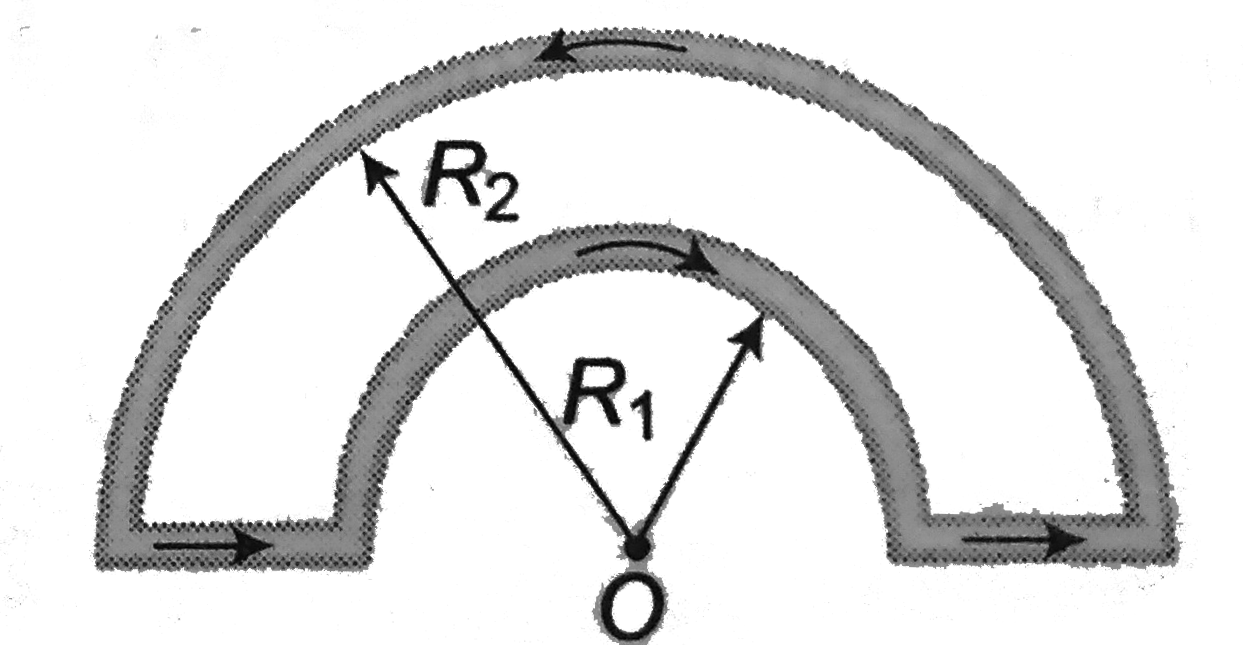
In the following figure magnetic field at mid point O due to sections 1,2,3 and 4 are considered as B1,B2,B3,B4 respectively.
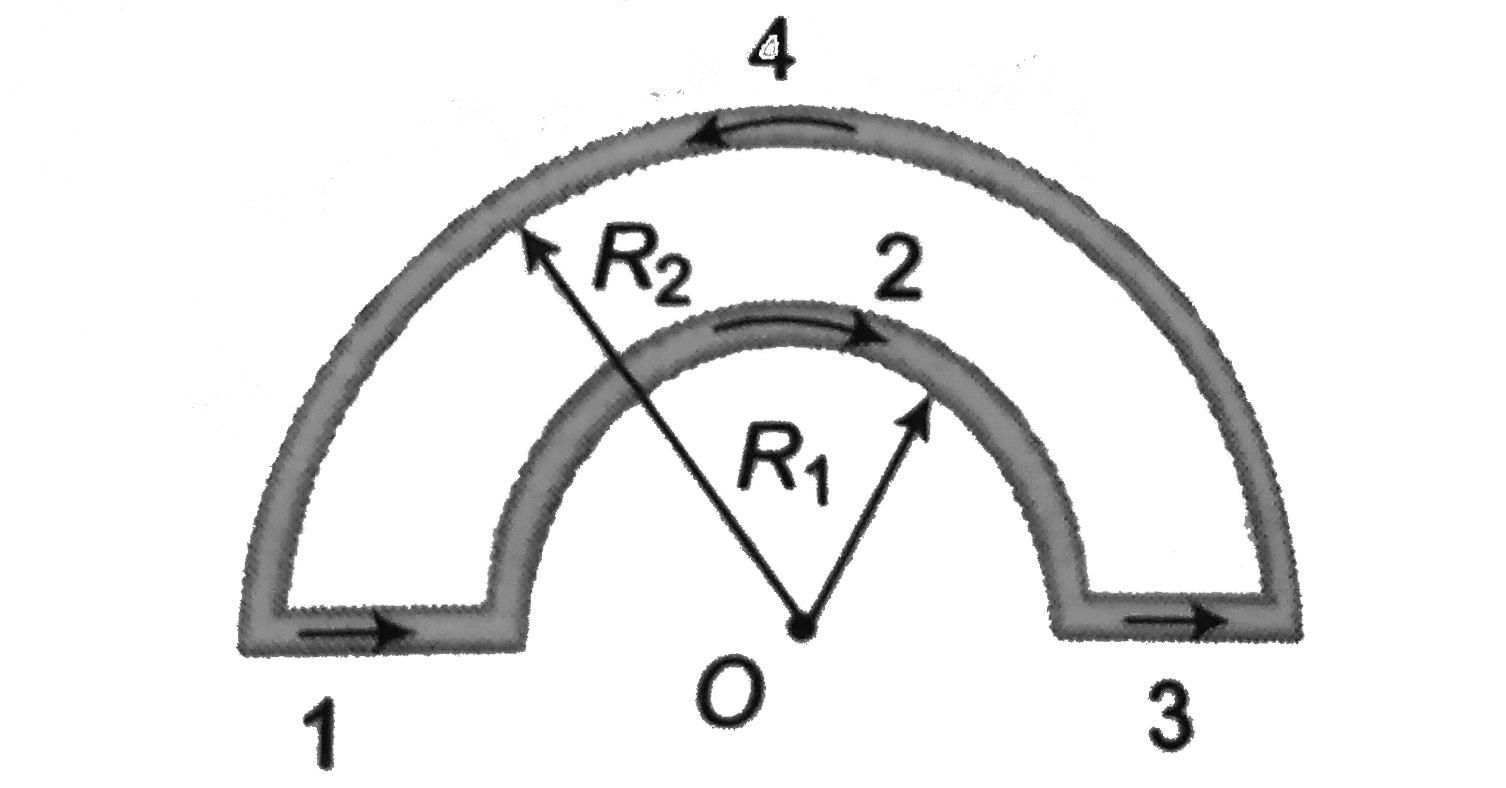
B1=B3=0
B2=μ04π.πiR1⊗
B4=μ04π.πiR2⊙ As |B2|>|B4|
So Bnet=B2−B4⇒Bnet=μ0i4(1R1−1R2)⊗
|
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Problems Based On Mixed Concepts
32 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning
31 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Current
44 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Knowledge Check
The magnetic induction at centre O Fig.
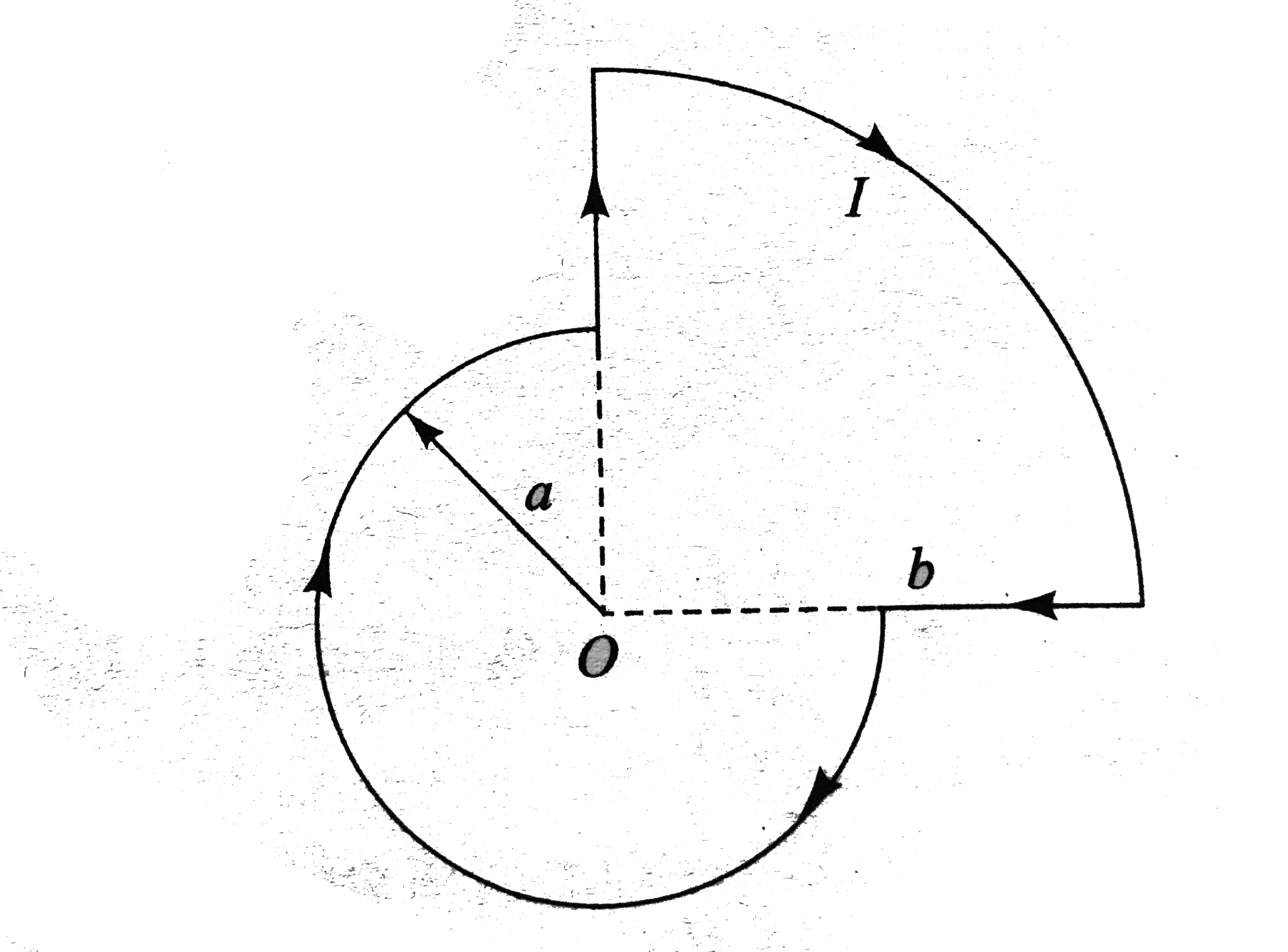 Aμ0I2a+μ0I2b⊗B3μ0I8a+μ0I8b⊗C3μ0I8a−μ0I8b⊗D3μ0I8a+μ0I8b⊙
Aμ0I2a+μ0I2b⊗B3μ0I8a+μ0I8b⊗C3μ0I8a−μ0I8b⊗D3μ0I8a+μ0I8b⊙The magnetic induction at center O as shown in the figure is
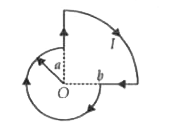 Aμ0I2a+μ0I2b⊗B3μ0I8a+μ0I8b⊗C3μ0I8a−μ0I8b⊗D3μ0I8a+μ0I8b⊙
Aμ0I2a+μ0I2b⊗B3μ0I8a+μ0I8b⊗C3μ0I8a−μ0I8b⊗D3μ0I8a+μ0I8b⊙Find the magnetic induction at the origin in the figure shown.
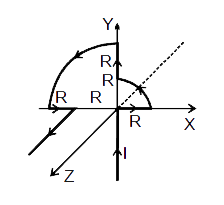 Aμ0I2R(34ˆk+1πˆj)Bμ0I4R(34ˆk+1πˆj)Cμ0I3R(34ˆk+1πˆj)Dμ0I4R(12ˆk+1πˆj)
Aμ0I2R(34ˆk+1πˆj)Bμ0I4R(34ˆk+1πˆj)Cμ0I3R(34ˆk+1πˆj)Dμ0I4R(12ˆk+1πˆj)
The magnetic induction at centre O in the following figure will be

View SolutionThe magnetic field at the centre O of the are shown in the figure is

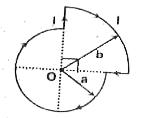
View SolutionMagnetic induction at the point O in the adjacent figure is
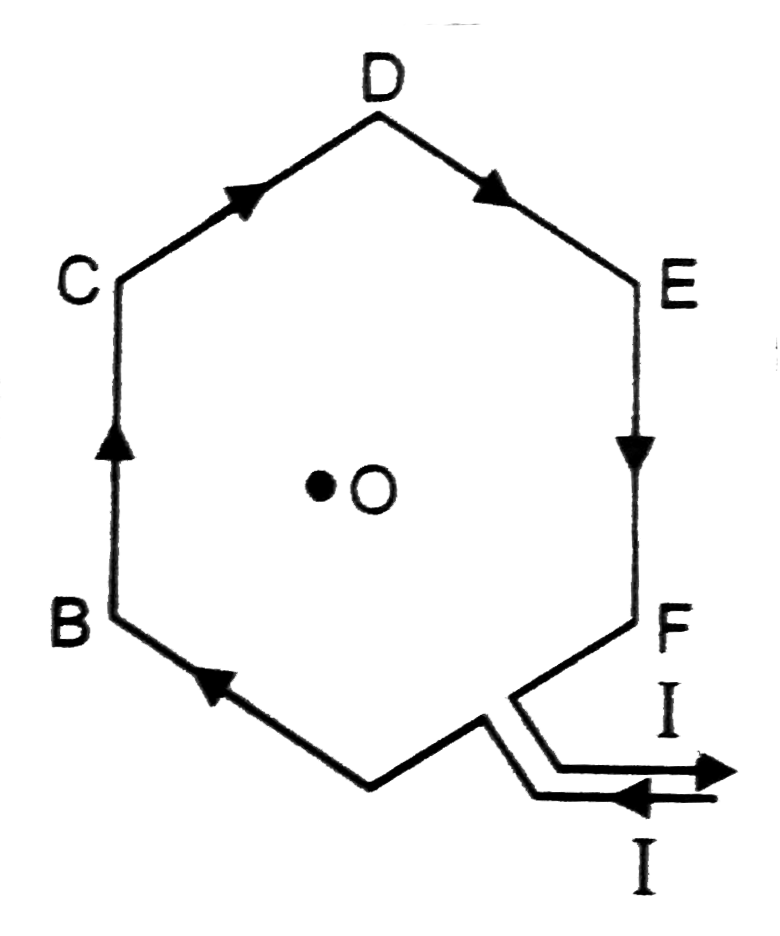
View SolutionA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
View SolutionA current I is flowing in an octagonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
View Solution