The magnitude of the magnetic field at the centre of the tightly wound 150 turn coil of radius 12 cm carrying a current of 2 A is
18G
19.7G
15.7G
17.7G
The correct Answer is:C
To find the magnitude of the magnetic field at the center of a tightly wound coil, we can use the formula for the magnetic field B at the center of a circular coil:
B=μ0NI2R
where:
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- N is the number of turns in the coil,
- I is the current in amperes,
- R is the radius of the coil in meters.
1. Identify the given values:
- Number of turns N=150
- Radius R=12cm=12×10−2m
- Current I=2A
2. Substitute the values into the formula:
B=μ0NI2R
Substituting the known values:
B=(4π×10−7)×150×22×(12×10−2)
3. Simplify the expression:
- First, calculate 2R:
2R=2×(12×10−2)=24×10−2=0.24m
- Now substitute this back into the equation:
B=(4π×10−7)×150×20.24
4. Calculate the numerator:
- Calculate 4π×150×2:
4π×150×2=1200π≈3769.91
- Therefore:
B=3769.91×10−70.24
5. Calculate the final value of B:
- Divide 3769.91×10−7 by 0.24:
B≈15624.63×10−7T=1.562463×10−3T
6. Convert to Gauss:
- Since 1T=104G:
B≈1.562463×10−3×104G=15.62463G
- Rounding to two decimal places gives:
B≈15.7G
Final Answer:
The magnitude of the magnetic field at the center of the coil is approximately 15.7 G.
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- N is the number of turns in the coil,
- I is the current in amperes,
- R is the radius of the coil in meters.
- Number of turns N=150
- Radius R=12cm=12×10−2m
- Current I=2A
B=μ0NI2R
Substituting the known values:
B=(4π×10−7)×150×22×(12×10−2)
- First, calculate 2R:
2R=2×(12×10−2)=24×10−2=0.24m
- Now substitute this back into the equation:
B=(4π×10−7)×150×20.24
- Calculate 4π×150×2:
4π×150×2=1200π≈3769.91
- Therefore:
B=3769.91×10−70.24
- Divide 3769.91×10−7 by 0.24:
B≈15624.63×10−7T=1.562463×10−3T
- Since 1T=104G:
B≈1.562463×10−3×104G=15.62463G
- Rounding to two decimal places gives:
B≈15.7G
The magnitude of the magnetic field at the center of the coil is approximately 15.7 G.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
The magnetic moment associated with a circular coil of 35 turns and radius 25 cm, if it carries a current of 11 A is
A72.2Am2B70.5Am2C74.56Am2D75.56Am2
The magnetic field at the centre of the current carrying coil is
View SolutionThe ratio of the magnetic field at the centre of a current carrying coil of the radius a and at distance 'a' from centre of the coil and perpendicular to the axis of coil is
View SolutionThe magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
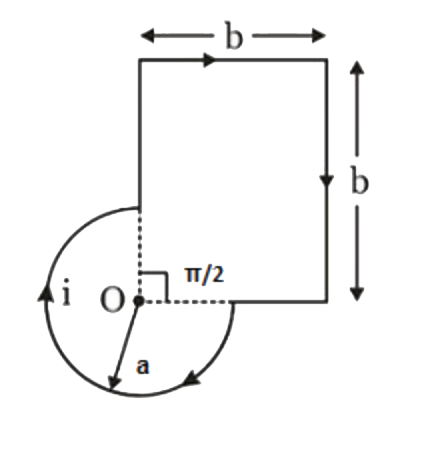 View Solution
View SolutionMagnitude of magnetic field (in SI units) at the centre of a hexagonal shape coil of side 10cm , 50 turns and carrying current I (Ampere) in units of μ0Iπ is :
View SolutionA circular coil of 200 turns has a radius of 10 cm and carries a current of 2.0 A. (a) Find the magnitude of the magnetic field (→B) at the centre of the coil. (b) At what distance from the centre along the axis of the coil will the field B drop to half its value at the centre?
View SolutionRatio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is
View SolutionThe magnetic field at the centre of a tightly wound spiral coil with inner radius R and outer radius 4.5 R with number of turns 22, when current i is flowing through it, is
View Solution

