The mass of hydrogen molecule is 3.23×1023 hydrogen molecules strike 2cm2 of a wall per second at an angle of 45∘ with the normal when moving with a speed of 105cms−1, what pressure do they exert on the wall ? Assume collision to be elasitc.
To solve the problem, we need to calculate the pressure exerted by hydrogen molecules on a wall when they collide with it at a specific angle and speed. Here’s a step-by-step solution:
Step 1: Identify Given Values
- Mass of a hydrogen molecule, m=3.32×10−27 kg
- Number of hydrogen molecules striking the wall per second, n=1023
- Area of the wall, A=2cm2=2×10−4m2
- Speed of the hydrogen molecules, v=105cm/s=103m/s
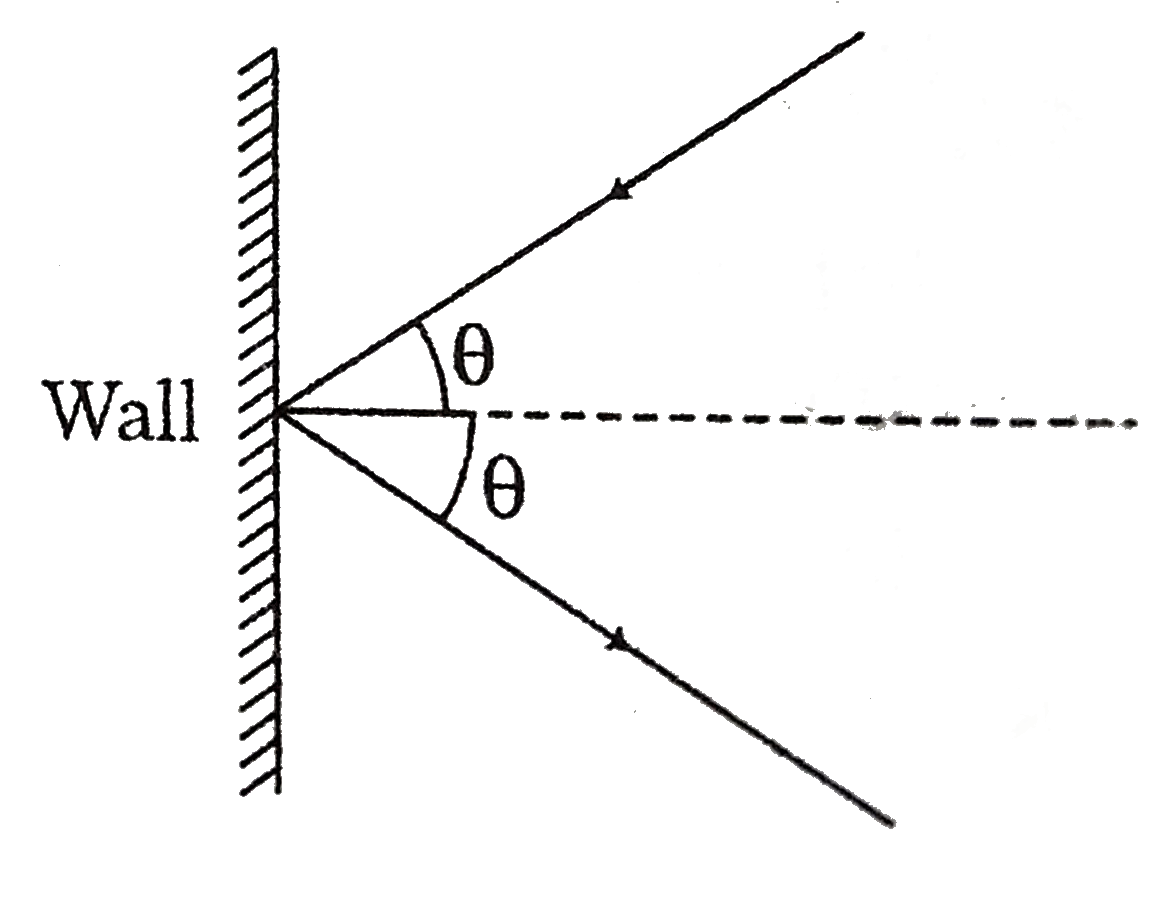
- Angle of incidence, θ=45∘
Step 2: Calculate the Change in Momentum
When a molecule strikes the wall and reflects back elastically, the change in momentum in the x-direction (the direction normal to the wall) can be calculated as follows:
1. The component of velocity in the x-direction before collision:
vx=vcos(θ)=v⋅1√2=103√2m/s
2. The change in momentum for one molecule:
Δp=m⋅(vx−(−vx))=m⋅(2vx)=2mvcos(θ)
Step 3: Calculate the Total Rate of Change of Momentum
The total rate of change of momentum for n molecules striking the wall per second is:
Total change in momentum=n⋅Δp=n⋅(2mvcos(θ))=n⋅2m⋅v√2
Step 4: Calculate the Force Exerted on the Wall
The force F exerted on the wall is equal to the total rate of change of momentum:
F=n⋅2m⋅v⋅cos(θ)
Step 5: Calculate the Pressure
Pressure P is defined as force per unit area:
P=FA=n⋅2m⋅v⋅cos(θ)A
Step 6: Substitute the Values
Now substituting the known values:
P=1023⋅2⋅(3.32×10−27)⋅(103)⋅1√22×10−4
Step 7: Simplify the Expression
1. The 2 in the numerator and denominator cancels out:
P=1023⋅(3.32×10−27)⋅(103)⋅1√210−4
2. Simplifying further:
P=1023⋅3.32×10−23⋅1√2=3.32√2×103N/m2
Step 8: Calculate the Final Value
Calculating 3.32√2:
√2≈1.414⇒3.321.414≈2.35
Thus,
P≈2.35×103N/m2
Final Answer
The pressure exerted by the hydrogen molecules on the wall is approximately:
2.35×103N/m2
- Mass of a hydrogen molecule, m=3.32×10−27 kg
- Number of hydrogen molecules striking the wall per second, n=1023
- Area of the wall, A=2cm2=2×10−4m2
- Speed of the hydrogen molecules, v=105cm/s=103m/s
- Angle of incidence, θ=45∘
When a molecule strikes the wall and reflects back elastically, the change in momentum in the x-direction (the direction normal to the wall) can be calculated as follows:
vx=vcos(θ)=v⋅1√2=103√2m/s
2. The change in momentum for one molecule:
Δp=m⋅(vx−(−vx))=m⋅(2vx)=2mvcos(θ)
The total rate of change of momentum for n molecules striking the wall per second is:
Total change in momentum=n⋅Δp=n⋅(2mvcos(θ))=n⋅2m⋅v√2
The force F exerted on the wall is equal to the total rate of change of momentum:
F=n⋅2m⋅v⋅cos(θ)
Pressure P is defined as force per unit area:
P=FA=n⋅2m⋅v⋅cos(θ)A
Now substituting the known values:
P=1023⋅2⋅(3.32×10−27)⋅(103)⋅1√22×10−4
1. The 2 in the numerator and denominator cancels out:
P=1023⋅(3.32×10−27)⋅(103)⋅1√210−4
P=1023⋅3.32×10−23⋅1√2=3.32√2×103N/m2
Calculating 3.32√2:
√2≈1.414⇒3.321.414≈2.35
Thus,
P≈2.35×103N/m2
The pressure exerted by the hydrogen molecules on the wall is approximately:
2.35×103N/m2
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Solved Examples
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.1
20 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
Similar Questions
Calculate weight of 3.011×1023 molecules of SO2?
View SolutionA parallel beam of nitrogen molecules moving with velocity v=400ms−1 imprings on a wall at an angle θ=30∘ to its normal. The concentration of molecules in the beam is n=9×1018cm−3. Find the pressure exerted by the beam on the wall, assuming that collisions are perfectly elastic.
View Solution
Knowledge Check
The mass of hydrogen molecule is 3.23×10−27Kg. If 1023 hydrogen molecules strike 2cm2 of a wall per second at an angle of 45∘ with the normal when moving with a speed of 105cms−1, what pressure do they exert on the wall ? Assume collision to be elastic.
A1350N/m2B2350N/m2C3320N/m2D1660N/m2The mass of hydrogen molecule is 3.32×10−27 kg. If 1023 hydrogen molecules strick per second at 2 cm2 area of a rigid wall at an angle of 45∘ from the normal and rebound back with a speed of 1000 ms−1, then the pressure ezxeted on the wass is
 A2.34×103 PaB0.23×106PaC0.23×103PaD23.4×103Pa
A2.34×103 PaB0.23×106PaC0.23×103PaD23.4×103Pa1023 molecules of a gas, each having a mass of 3×10−27 kg strike per second per sq. cm. of a rigid will at an angle of 60∘ with the normal and rebound with a velocity of 500m/s. What is the pressure exerted by the gas molecules on the wall?
A500N/m2B1000N/m2C1500N/m2D2000N/m2
The mass of a molecule of gas is 4×10−30kg.If1023 molecules strike the area of 4 square meter with the velocity 107 m/sec, then what is the pressure exerted on the surface ?
(Assuming perfectly elastic collision and they are hitting perpendicularly)
View SolutionA body of mass 3 kg hits a wall at an angle of 60∘ & returns at the same angle. The impact time was 0.2s. Calculate the force exerted on the wall:
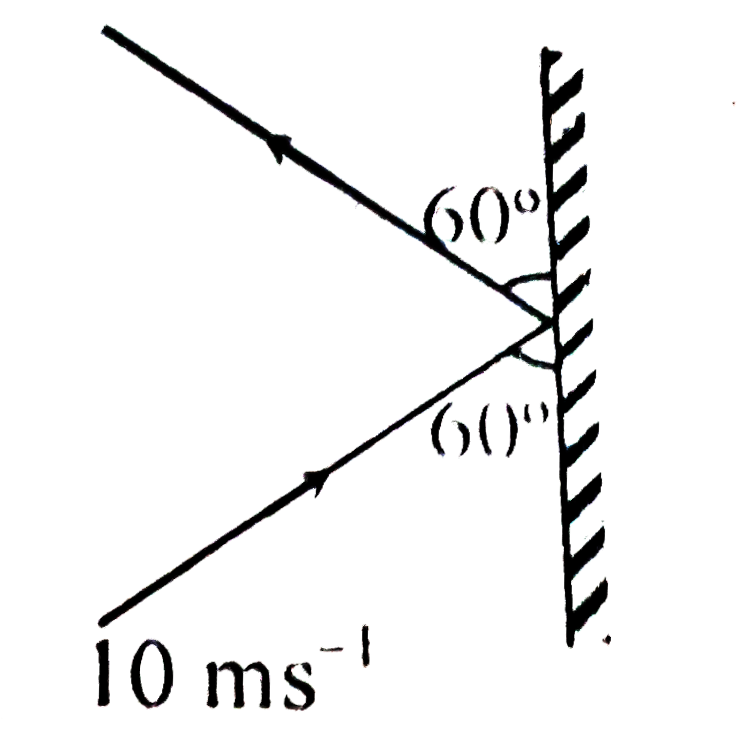
View SolutionWhat mass of carbon dioxide (CO2) will contain 3.011×1023 molecules?
View SolutionWhat mass of (NH4)2CO3 with contains 6.022×1023 hydrogen atoms?
View SolutionWhat mass of carbon dioxide (CO2) will contain 3.011×1023 molecules?
View Solution
