The maximum current in a galvanometer can be 10 mA. Its resistance is . To convert it into an ammeter of 1 A, what resistance should be connected in parallel with galvanometer (in ?
The correct Answer is:A
To solve the problem of converting a galvanometer into an ammeter, we need to determine the resistance that should be connected in parallel with the galvanometer. Here’s a step-by-step solution:
Step 1: Understand the Given Values
- Maximum current in the galvanometer, Ig=10mA=10×10−3A
- Resistance of the galvanometer, Rg=10Ω
- Desired maximum current for the ammeter, I=1A
Step 2: Use the Formula for Shunt Resistance
When a galvanometer is converted into an ammeter, a shunt resistance S is connected in parallel. The relationship between the currents is given by:
I=Ig+Is
where Is is the current through the shunt. The potential difference across both the galvanometer and the shunt is the same:
IgRg=IsS
Step 3: Express Is in Terms of I and Ig
From the first equation, we can express Is:
Is=I−Ig
Step 4: Substitute Is into the Voltage Equation
Substituting Is into the voltage equation gives:
IgRg=(I−Ig)S
Step 5: Rearrange to Solve for S
Rearranging the equation to solve for S:
S=IgRgI−Ig
Step 6: Substitute the Known Values
Now, substitute Ig=10×10−3A, Rg=10Ω, and I=1A:
S=(10×10−3)×101−(10×10−3)
Step 7: Calculate the Values
Calculating the numerator:
(10×10−3)×10=0.1
Calculating the denominator:
1−10×10−3=1−0.01=0.99
Thus,
S=0.10.99≈0.10101Ω
Step 8: Convert to the Required Format
Since the problem asks for the answer in 10−1Ω:
S≈0.10101Ω≈100Ω (approximately)
Thus, we can express it as:
S≈1.01×10−1Ω
Final Answer
To convert the galvanometer into an ammeter of 1 A, the resistance that should be connected in parallel with the galvanometer is approximately:
S≈10−1Ω
- Maximum current in the galvanometer, Ig=10mA=10×10−3A
- Resistance of the galvanometer, Rg=10Ω
- Desired maximum current for the ammeter, I=1A
When a galvanometer is converted into an ammeter, a shunt resistance S is connected in parallel. The relationship between the currents is given by:
I=Ig+Is
where Is is the current through the shunt. The potential difference across both the galvanometer and the shunt is the same:
IgRg=IsS
From the first equation, we can express Is:
Is=I−Ig
Substituting Is into the voltage equation gives:
IgRg=(I−Ig)S
Rearranging the equation to solve for S:
S=IgRgI−Ig
Now, substitute Ig=10×10−3A, Rg=10Ω, and I=1A:
S=(10×10−3)×101−(10×10−3)
Calculating the numerator:
(10×10−3)×10=0.1
Calculating the denominator:
1−10×10−3=1−0.01=0.99
Thus,
S=0.10.99≈0.10101Ω
Since the problem asks for the answer in 10−1Ω:
S≈0.10101Ω≈100Ω (approximately)
Thus, we can express it as:
S≈1.01×10−1Ω
To convert the galvanometer into an ammeter of 1 A, the resistance that should be connected in parallel with the galvanometer is approximately:
S≈10−1Ω
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A galvanometer of resistance 1000Ω gives full-scale deflection for a current of 1mA. To measure a P.D of 10V, the resistance to be connected with the galvanometer is
View SolutionThe deflection of a galvanometer falls to 1/10th when a resistance of 5Ω is connected in parallel with it. If an additional resistance of 2Ω is connected in parallel to the galvanometer, the deflection is
View Solution
Knowledge Check
- Question 1 - Select One
A galvanometer of resistance 70Ω, is converted to an ammeter by a shunt resistance r3=0.03Ω. The value of its resistance will become
A0.025ΩB0.022ΩC0.035ΩD0.030Ω
The full scale deflection current of a galvanometer of resistance 1Ω is 5mA. How will you convert it into a voltmeter of range of 5V?
View SolutionA milliammeter of range 10mA has a coli of resistance 1Ω. To use it as an ammeter of range 1A, the required shunt must have a resistance of
View SolutionIn the given circuit, a galvanometer with a resistance of 70Ω is converted to an ammeter 0.05Ω by a shunt resistance of 0.052, total current measured by this device
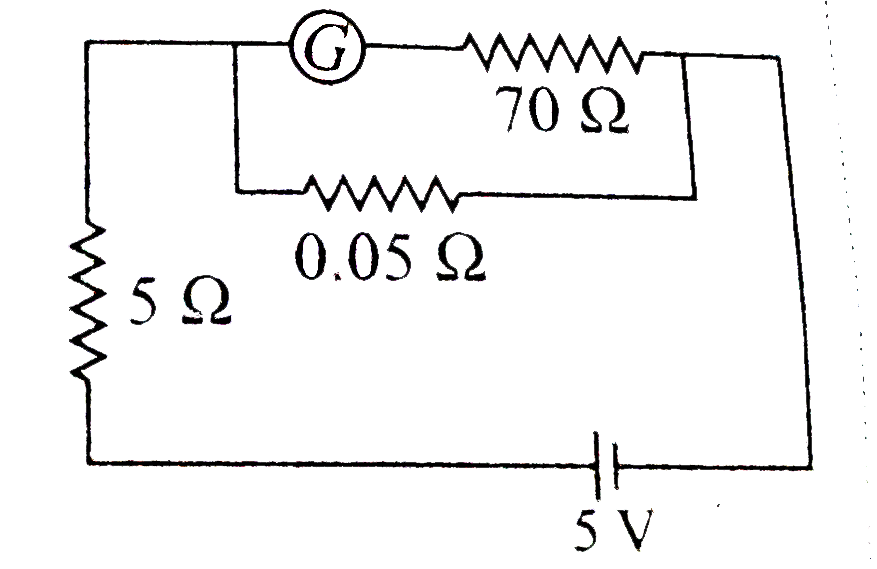 View Solution
View SolutionA galvanometer has resistance 1Ω. Maximum deflection current through it is 0.1 A
View SolutionWhen a current of 5mA is passed through a galvanometer having a coil of resistance 15Ω, it shows full sacle deflection. The value of the resistance to be put in series with the galvanometer to convert it into a voltmeter of range 0−10V is:
View SolutionA maximum current of 0.5 mA can be passed through a galvanometer of resistance 20Ω. Calculate the resistance to be connected in series to convert it into a voltmeter of range (0−5)V.
View SolutionIn full scale deflection current in galvanometer of 100ohm resistance is 1 mA. Resistance required in series to convert it into voltmeter of range 10 V.
View Solution

