Question

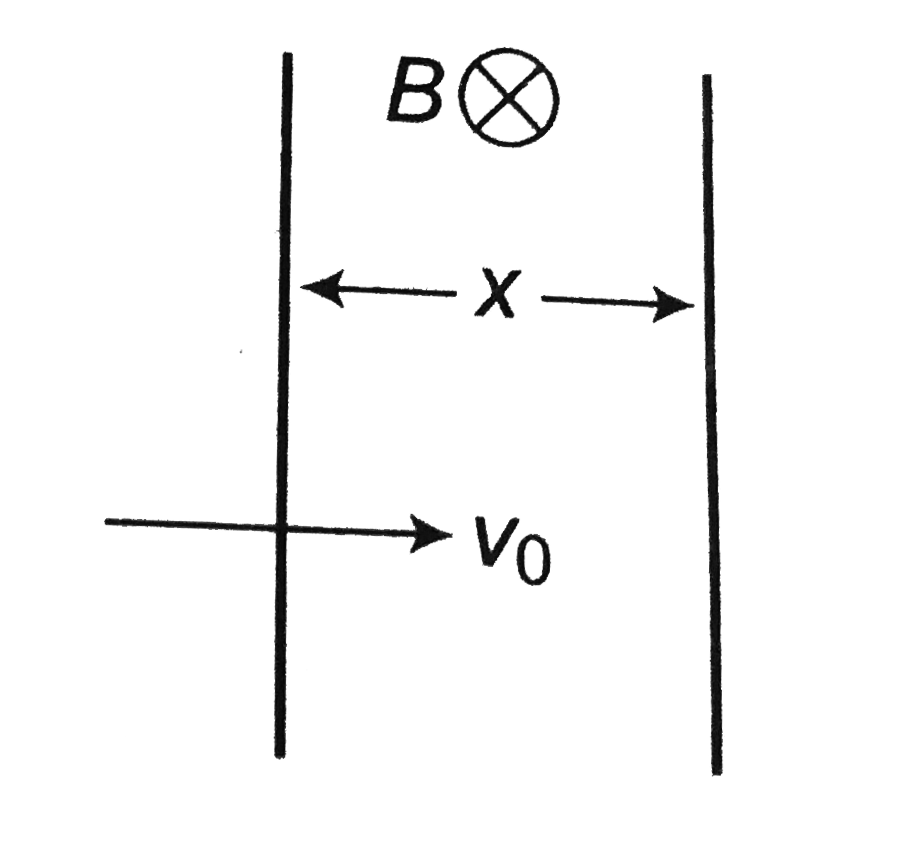
A charged particle enters a uniform magnetic field with velocity $v_0=4m/s$ perpendicular to it, the length of magnetic field is $x=\left(\frac{\sqrt{3}}{2}\right)R$, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.

Answer

4

Explanation

To solve the problem step by step, we will analyze the motion of a charged particle in a magnetic field and derive the final velocity when it exits the field.

Step 1: Understanding the Motion
When a charged particle enters a uniform magnetic field perpendicularly, it moves in a circular path due to the magnetic force acting on it. The radius \( R \) of the circular path is determined by the particle's velocity \( v_0 \) and the magnetic field \( B \).

Step 2: Given Parameters
- Initial velocity \( v_0 = 4 \, \text{m/s} \)
- Length of the magnetic field \( x = \frac{\sqrt{3}}{2} R \)

Step 3: Finding the Radius of the Circular Path
The radius \( R \) of the circular path can be expressed in terms of the magnetic field \( B \) and the charge \( q \) of the particle using the formula:
\( R = \frac{mv_0}{qB} \)
where \( m \) is the mass of the particle.

Step 4: Finding the Angle
From the given length of the magnetic field \( x \), we can relate it to the angle \( \theta \) subtended by the circular path:
\( x = R \theta \)
Given \( x = \frac{\sqrt{3}}{2} R \), we can write:
\( R \theta = \frac{\sqrt{3}}{2} R \)
This implies:
\( \theta = \frac{\sqrt{3}}{2} \)
To find \( \theta \) in degrees, we can convert:
\( \theta = 60^\circ \)

Step 5: Velocity Components
When the particle exits the magnetic field, we can resolve the velocity into components. The new velocity \( v_1 \) can be expressed as:
\( v_1 = v_0 \cos(60^\circ) \hat{i} + v_0 \sin(60^\circ) \hat{j} \)
Substituting \( v_0 = 4 \, \text{m/s} \):
\( v_1 = 4 \cdot \frac{1}{2} \hat{i} + 4 \cdot \frac{\sqrt{3}}{2} \hat{j} \)
This simplifies to:
\( v_1 = 2 \hat{i} + 2\sqrt{3} \hat{j} \)

Step 6: Magnitude of the Final Velocity
To find the magnitude of the final velocity \( v_1 \):
\( |v_1| = \sqrt{(2)^2 + (2\sqrt{3})^2} \)
Calculating this gives:
\( |v_1| = \sqrt{4 + 12} = \sqrt{16} = 4 \, \text{m/s} \)

Final Answer
The magnitude of the velocity of the particle when it comes out of the field is \( 4 \, \text{m/s} \).

---