The maximum load that a wire can sustain is W. If the wire is cut to half its value, the maximum load it can sustain is
W
W2
W4
2W
The correct Answer is:A
To solve the problem, we need to understand how the maximum load a wire can sustain is related to its physical properties, particularly its length and cross-sectional area.
1. Understanding the Maximum Load:
The maximum load W that a wire can sustain is determined by the formula:
Fmax=σ⋅A
where σ is the stress (which is the maximum load per unit area), and A is the cross-sectional area of the wire.
2. Cutting the Wire:
When the wire is cut to half its length, the new length of the wire becomes L/2. The cross-sectional area A remains unchanged.
3. Stress and Maximum Load:
The stress σ in the wire is defined as:
σ=FmaxA
Since the wire is made of the same material and has the same cross-sectional area, the maximum stress that the wire can handle remains the same.
4. Maximum Load After Cutting:
If we denote the maximum load after cutting the wire as W′, we can express it as:
W′=σ⋅A
Since σ does not change and A remains the same, we can conclude that:
W′=W
5. Conclusion:
Therefore, even after cutting the wire to half its length, the maximum load it can sustain remains the same, which is W.
Final Answer:
The maximum load that the wire can sustain after being cut to half its length is W.
---
The maximum load W that a wire can sustain is determined by the formula:
Fmax=σ⋅A
where σ is the stress (which is the maximum load per unit area), and A is the cross-sectional area of the wire.
When the wire is cut to half its length, the new length of the wire becomes L/2. The cross-sectional area A remains unchanged.
The stress σ in the wire is defined as:
σ=FmaxA
Since the wire is made of the same material and has the same cross-sectional area, the maximum stress that the wire can handle remains the same.
If we denote the maximum load after cutting the wire as W′, we can express it as:
W′=σ⋅A
Since σ does not change and A remains the same, we can conclude that:
W′=W
Therefore, even after cutting the wire to half its length, the maximum load it can sustain remains the same, which is W.
The maximum load that the wire can sustain after being cut to half its length is W.
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 1 Subjective
8 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Single Correct
10 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Assertion And Reason
22 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
Knowledge Check
The maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will
Abe doubleBbe halfCbe four timesDremain same.
A cable that can support a load W is cut into two equal parts .T he maximum load that can be supported by either part is
View SolutionThe maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will
View SolutionA wire of cross-sectional area A breaks due to its own weight when length of the wire is l. If area of cross-section of the wire is made 3A then maximum length of the wire can be hung without breaking is
View SolutionWhat happens to the (i) extension (ii) maximum load, a wire can bear, when the wire is cut into half?
View SolutionThe length of a wire is increased by 1mm on the application, of a given load. In a wire of the same material, but of length and radius twice that of the first, on application of the same load, extension is
View SolutionA steel cable with a radius of 1.5 cm support a chairlift at a ski area.if the maximum stress is not to exceed 108Nm−2, what is the maximum load the cable can support?
View SolutionAn ideal diode is connected in a circuit with resistance R=50ΩandV=10V. If an AC input signal shown in the figure is given to the circuit, then the maximum and minimum value of output voltage (without load) is
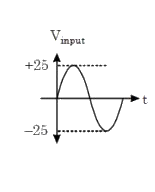
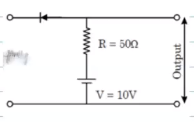
View Solution
