A steel cable with a radius of 1.5 cm support a chairlift at a ski area.if the maximum stress is not to exceed 108Nm−2, what is the maximum load the cable can support?
To find the maximum load that the steel cable can support, we will follow these steps:
Step 1: Convert the radius from centimeters to meters
The radius of the cable is given as 1.5 cm. To convert this to meters:
Radius=1.5cm=1.5×10−2m=0.015m
Step 2: Identify the maximum stress
The maximum stress that the cable can withstand is given as:
Maximum Stress=108N/m2
Step 3: Calculate the area of the cross-section of the cable
The area A of the cross-section of the cable (which is circular) can be calculated using the formula:
A=πr2
Substituting the radius:
A=π(0.015)2
Calculating this gives:
A≈π×0.000225≈0.00070686m2
Step 4: Calculate the maximum force using the formula for stress
The relationship between stress, force, and area is given by:
Stress=ForceArea
Rearranging this to find the maximum force F:
F=Stress×Area
Substituting the known values:
F=108N/m2×0.00070686m2
Calculating this gives:
F≈70686N≈7.065×104N
Conclusion
The maximum load that the cable can support is approximately:
Maximum Load≈70686N or 7.065×104N
---
The radius of the cable is given as 1.5 cm. To convert this to meters:
Radius=1.5cm=1.5×10−2m=0.015m
The maximum stress that the cable can withstand is given as:
Maximum Stress=108N/m2
The area A of the cross-section of the cable (which is circular) can be calculated using the formula:
A=πr2
Substituting the radius:
A=π(0.015)2
Calculating this gives:
A≈π×0.000225≈0.00070686m2
The relationship between stress, force, and area is given by:
Stress=ForceArea
Rearranging this to find the maximum force F:
F=Stress×Area
Substituting the known values:
F=108N/m2×0.00070686m2
Calculating this gives:
F≈70686N≈7.065×104N
The maximum load that the cable can support is approximately:
Maximum Load≈70686N or 7.065×104N
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- MOTION IN A PLANE BOOK - NCERT ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXERCISE
32 Videos
Similar Questions
A massive stone pillar 20m high and of uniform cross section rests on a rigid base and supports a vertical load of 5.0×105N at its upper end. If the compressive stress in the pillar is not exceed 1.6×106N/m2, what is the minimum cross-sectional area of the pillar? (Density of the stone =2.5×103kg/m3 take g=10N/kg)
View SolutionA cable is cut to half of its original length. Why does this change has no effect on the maximum load that it can support?
View Solution
Knowledge Check
A steel cable with a radius 2 cm supports a chairlift at a ski area. If the maximum stress is not to exceed 108Nm−2, the maximam load the cable can support
A4π×105NB4π×104NC2π×105ND2π×104
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6 mm. Assume that each rivet is to carry one quarter of the load. If the shearing stress on the rivet is not to exceed 6.9×107Pa, the maximum tension that can be exerted by the riveted strip is
View SolutionTwo long metallic strips are joined together by two rivets each of radius 2mm. Each rivet can withstand a maximum shearing stress of 1.5×109N/m2. Assuming that each rivet shares the stretching load equally, the maximum tensile force the strip can exert without rupture is
View SolutionTwo long metallic strips are joined together by two rivets each of radius 2mm. Each rivet can withstand a maximum shearing stress of 1.5×109N/m2. Assuming that each rivet shares the stretching load equally, the maximum tensile force the strip can exert without rupture is
View SolutionA cable that can support a load W is cut into two equal parts .T he maximum load that can be supported by either part is
View SolutionA steal wire of cross-section area 3×10−6m2 can withstand a maximum strain of 10−3 .Young's modulus of steel is 2×1011Nm−2 .The maximum mass this wire can hold is
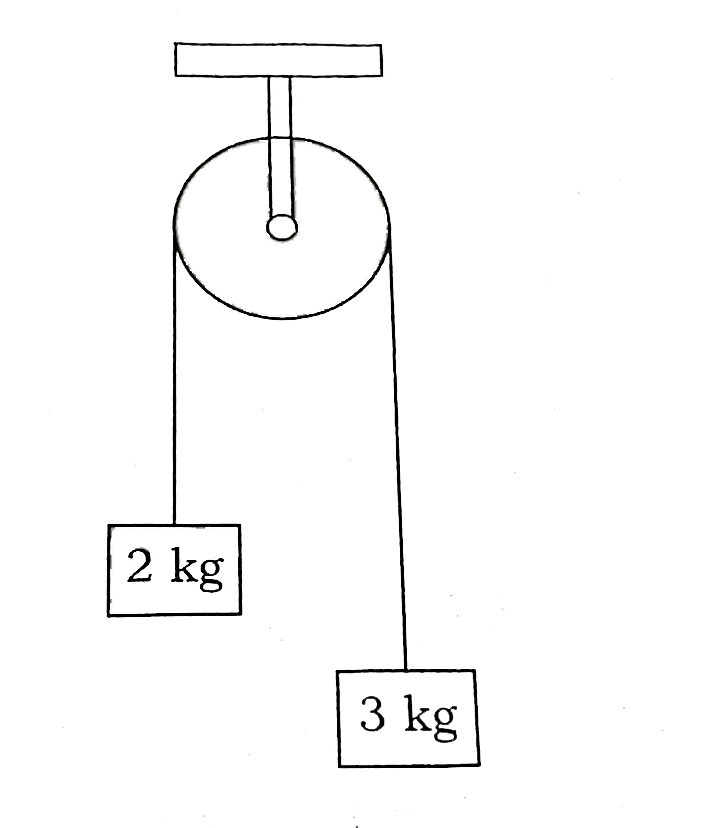
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
View SolutionA 10 kg mass is attached to a string that has a breaking strength of 1,500 N. if the mass is whirled in a horizontal circle of radius 90 cm, what is the maximum speed it can have ? (Neglect the effects of gravity).
View Solution
