The maximum potential energy of a simple harmonic oscilator is Umax. The the P.E. of the oscillator when it is half way to its end point is
A
Umax2
B
Umax3
C
Umax4
D
2Umax
Video Solution
Text Solution
The correct Answer is:C
P.E.atx=A2 is 12mω2×A24
∴P.E.=14[12mω2A2]=Umax4
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the total energy of a simple harmonic oscillator is E, then its potential energy, when it is halfway to its endpoint will be
A23FB18EC14ED12EThe variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
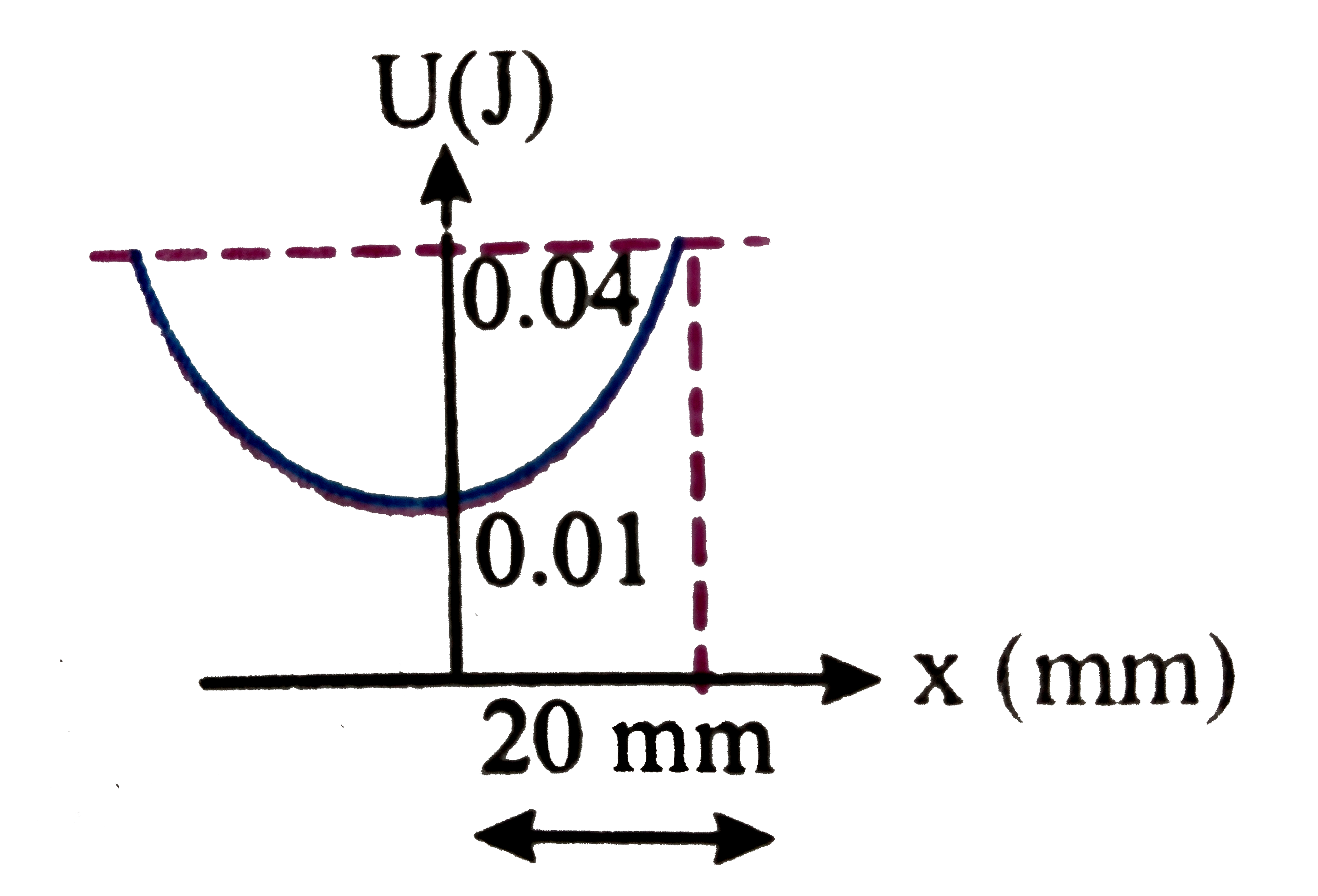 A100N/mB150N/mC2003N/mD300N/m
A100N/mB150N/mC2003N/mD300N/mThe potential energy of a simple harmonic oscillator of mass 2 kg in its mean position is 5 J. If its total energy is 9 J and its amplitude is 0.01 m, its time period would be
Aπ10sBπ20sCπ50sDπ100s
The maximum acceleration of a simple harmonic oscillator is a0 and maximum velocity is v0. What is the displacement amplitude?
View SolutionAt which position the kinetic energy of a harmonic oscillator is maximum or minimum ?
View SolutionAt which position the kinetic energy of a harmonic oscillator is maximum or minimum ?
View SolutionThe initial phase of a simple harmonic oscillator is zero. At what fraction of the period, the velocity is half of its maximum value?
View SolutionThe variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is
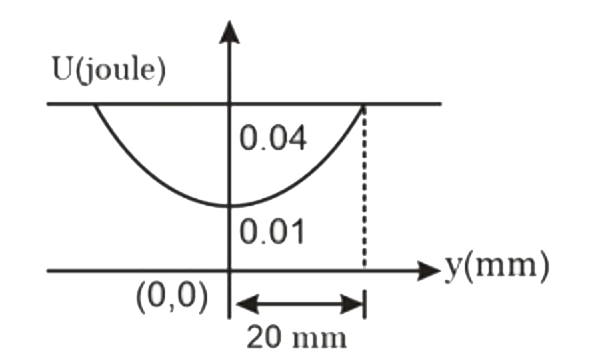
View Solution
