The measurement of an unknown resistance R is to be carried out using Wheatstone bridge (see Fig. 2(EP).3). Two students perform an experiment in two way. The first student takes R2=10Ω and R1=5Ω. The other student takes R2=1000Ω and R1=500Ω. In the standard arm, both take R3=5Ω. Both find R=R2R1R3=10Ω within errors.
The errors of measurement of the two students are the same
Errors of measurement do depends on the accuracy with which R2andR1 can be measured
If the student uses large values of R2andR1 The currents through the arms will be feeble. This will make determination of null point accurately more difficult
Wheatstone bridge is a very accurate instrument and has no errors of measurement
The correct Answer is:B, C
To solve the problem of measuring an unknown resistance R using a Wheatstone bridge, we can follow these steps:
Step 1: Understand the Wheatstone Bridge Configuration
The Wheatstone bridge consists of four resistors arranged in a diamond shape. The resistors are labeled as R1, R2, R3, and R (the unknown resistance). The bridge is balanced when the ratio of the resistances is equal, allowing us to calculate R.
Step 2: Write the Formula for the Wheatstone Bridge
The formula for the unknown resistance R when the bridge is balanced is given by:
R=R2R1R3
Step 3: Calculate R for the First Student
For the first student:
- R1=5Ω
- R2=10Ω
- R3=5Ω
Substituting these values into the formula:
R=105×5=2×5=10Ω
Step 4: Calculate R for the Second Student
For the second student:
- R1=500Ω
- R2=1000Ω
- R3=5Ω
Substituting these values into the formula:
R=1000500×5=2×5=10Ω
Step 5: Conclusion
Both students calculated the unknown resistance R to be 10Ω. This shows that the Wheatstone bridge can yield the same result even with different resistor values, as long as the ratios are maintained.
Step 6: Discuss the Errors
The errors in measurement can arise from inaccuracies in the resistors used. The first student's resistors are smaller, while the second student's resistors are larger. However, both students arrived at the same value of R within their respective measurement errors.
Final Answer
Thus, the unknown resistance R measured by both students is 10Ω.
---
The Wheatstone bridge consists of four resistors arranged in a diamond shape. The resistors are labeled as R1, R2, R3, and R (the unknown resistance). The bridge is balanced when the ratio of the resistances is equal, allowing us to calculate R.
The formula for the unknown resistance R when the bridge is balanced is given by:
R=R2R1R3
For the first student:
- R1=5Ω
- R2=10Ω
- R3=5Ω
R=105×5=2×5=10Ω
For the second student:
- R1=500Ω
- R2=1000Ω
- R3=5Ω
R=1000500×5=2×5=10Ω
Both students calculated the unknown resistance R to be 10Ω. This shows that the Wheatstone bridge can yield the same result even with different resistor values, as long as the ratios are maintained.
The errors in measurement can arise from inaccuracies in the resistors used. The first student's resistors are smaller, while the second student's resistors are larger. However, both students arrived at the same value of R within their respective measurement errors.
Thus, the unknown resistance R measured by both students is 10Ω.
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Integer
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type
7 Videos
Similar Questions
In the given circuit, R1 = 10Ω R2=6Ω and E = 10V, then correct statement is
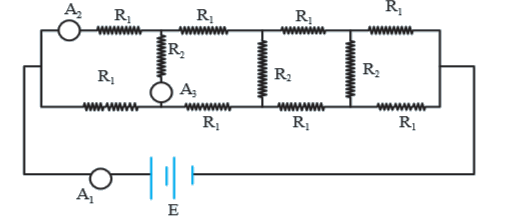
View SolutionIn the circuit shown in figure

Current through R2 is zero if R4=2Ω and R3=4Ω In this case
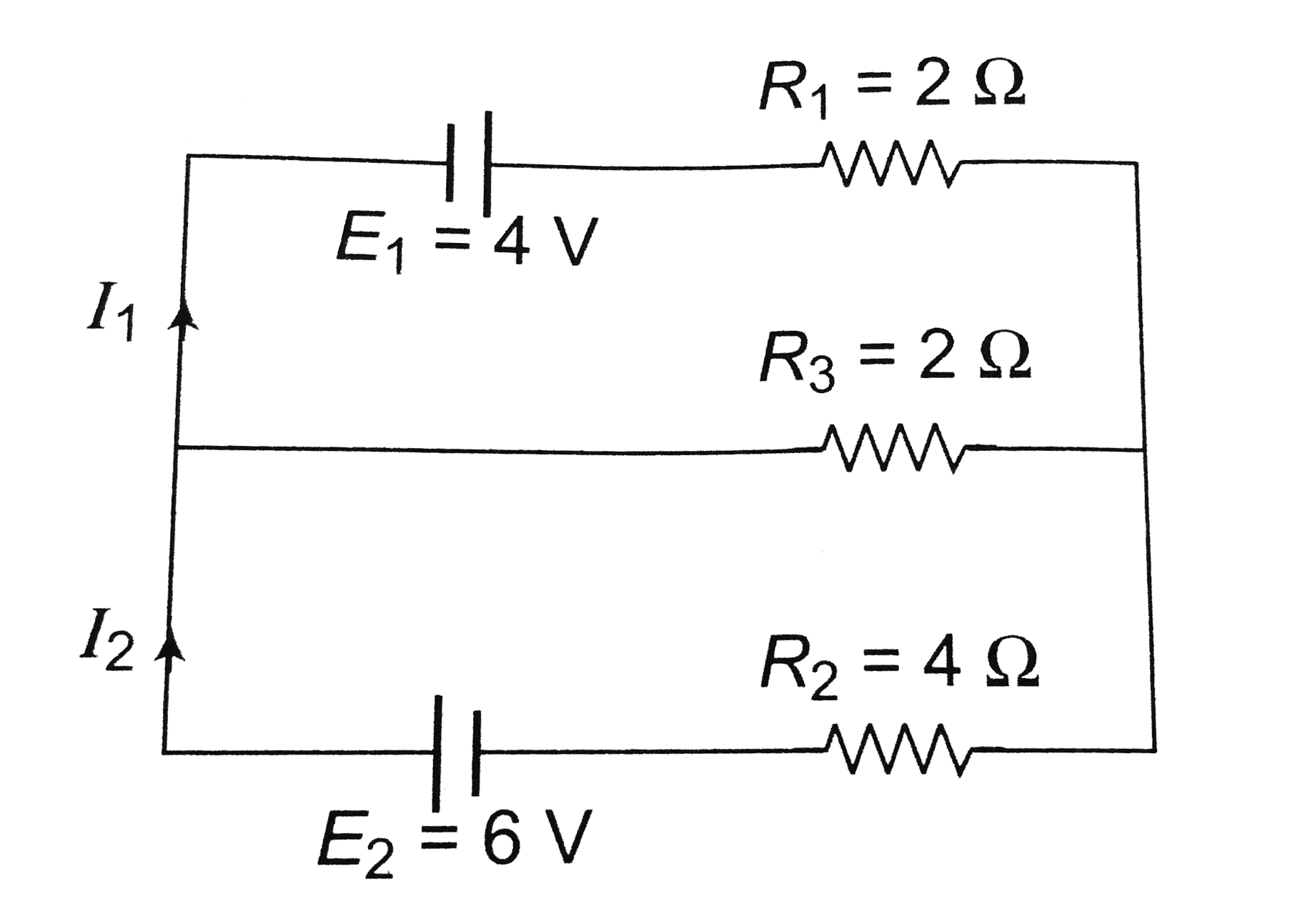
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
View SolutionThe potential difference in volt across the resistance R3 in the circuit shown in figure, is (R1=15Ω,R2=15Ω,R3=30Ω,R4=35Ω)

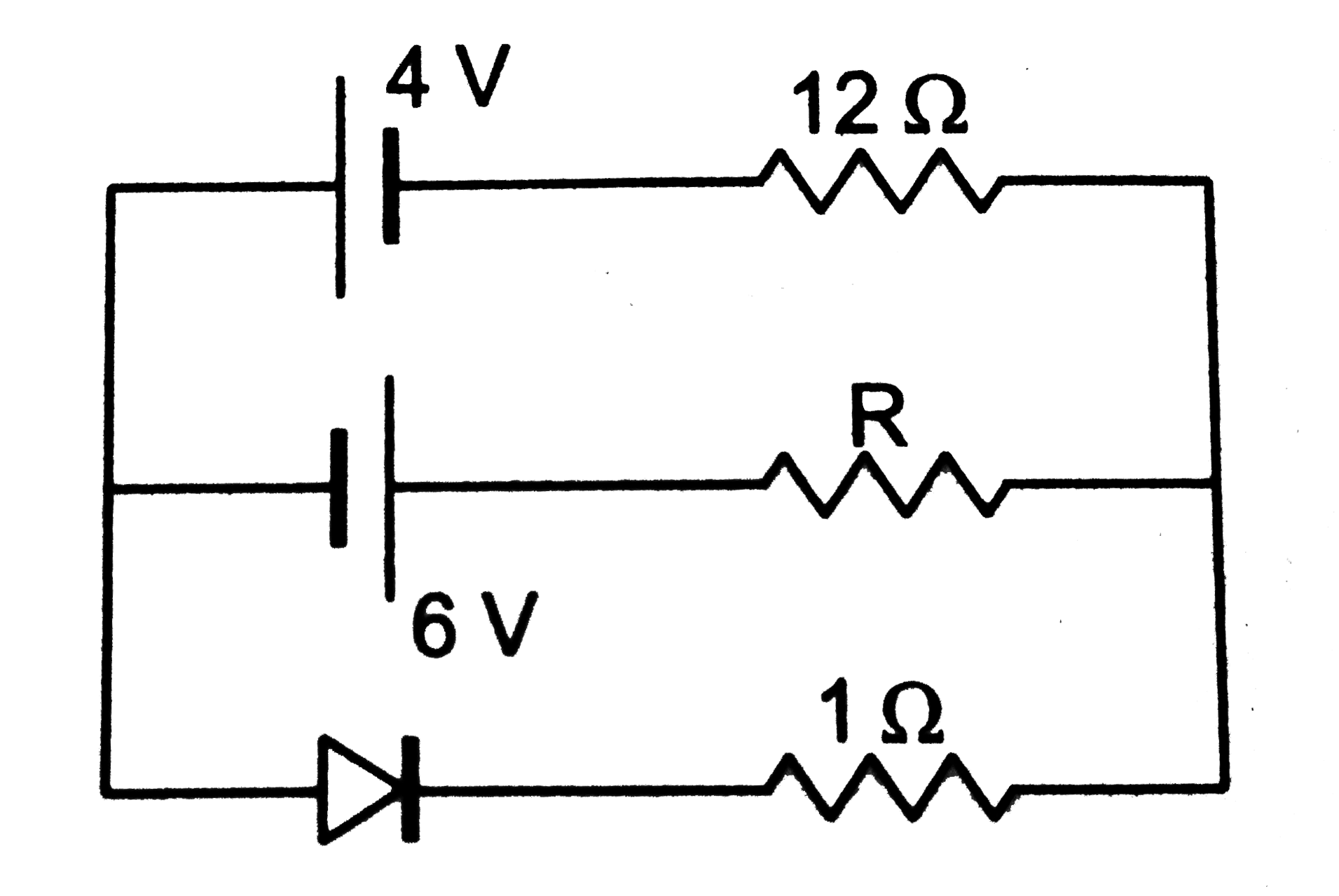
View SolutionFind the current through the resistance R in figure.If (a)R=12Ω(b)R=48Ω.
View SolutionIn the circuit shown in Fig. the emf of the sources is equal to ξ=5.0V and the resistances are equal to R1=4.0Ω and R2=6.0Ω. The internal resistance of the source equals R=1.10Ω. Find the currents flowing through the resistances R1 and R2.
View SolutionIn the given figure, E=12V, R1=3Ω,R2=2Ω and r=1Ω. The choose the correct option/s

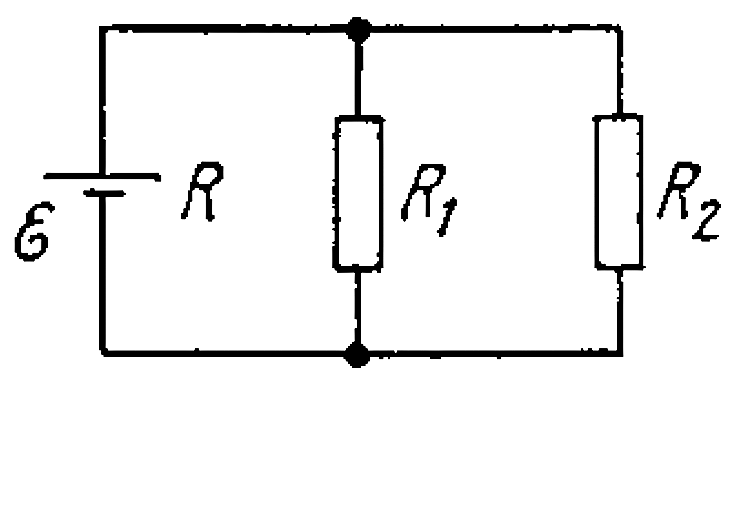
View SolutionA resistor of resistance R is connected to a cell internal resistance 5Ω. The value of R is varied from 1Ω to 5Ω. The power consumed by R
View SolutionConsider the circuit shown in fig.
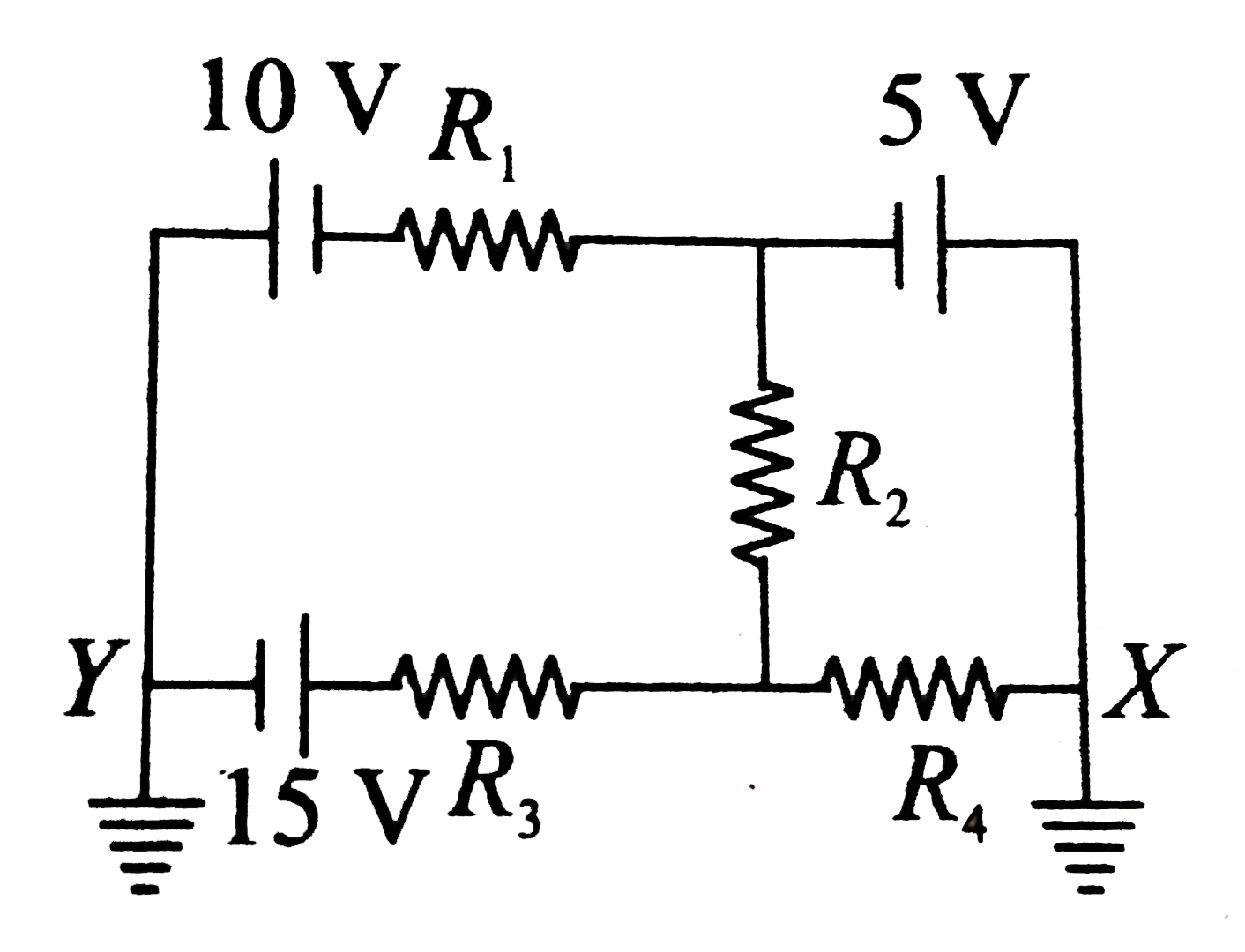
Current through R2 is zero if R4=2ΩandR3=4Ω in this case
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
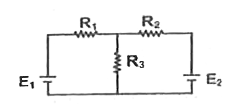
View Solution
