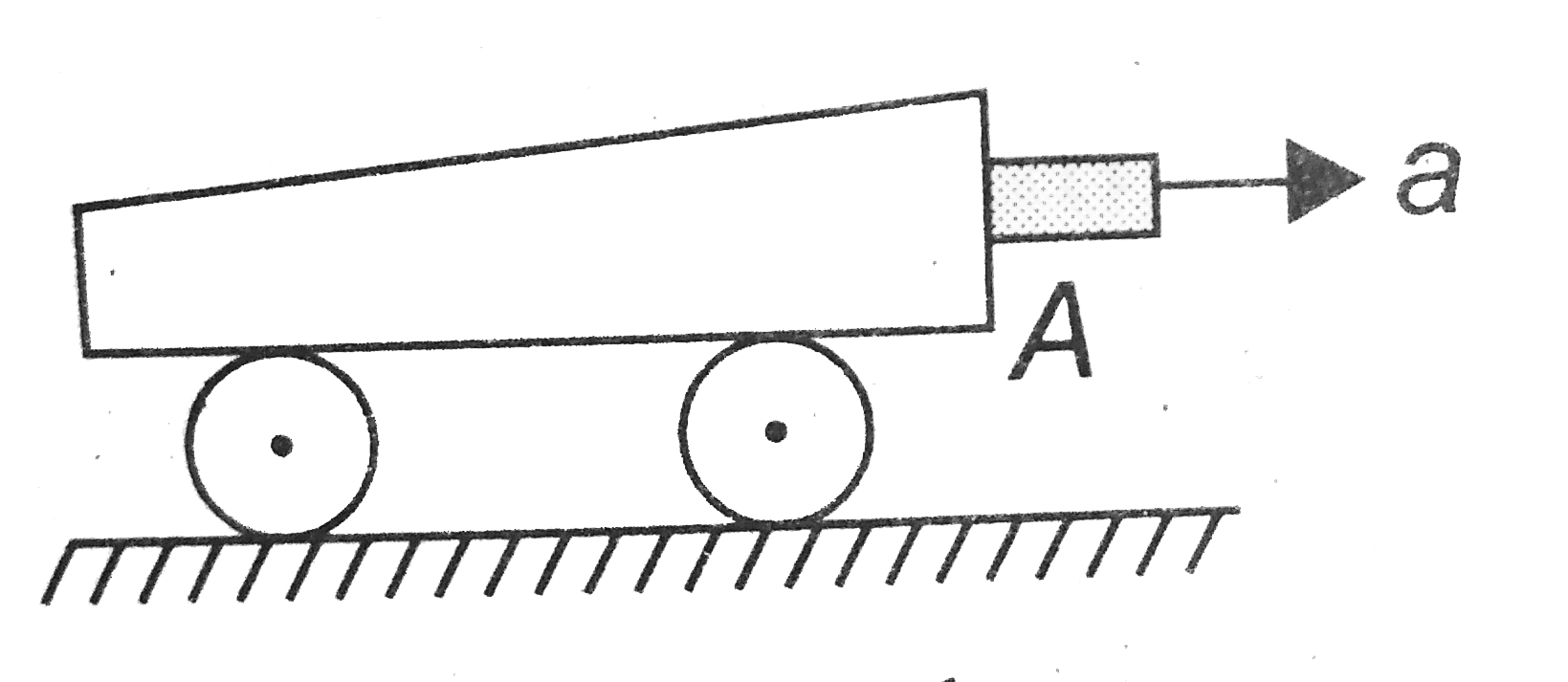
The minimum acceleration that must be impprted to the cart in the figure so that the block A will not fall (given μ is the coefficient if friction between the surface of block and cart) is given by:
a<gμ
a>mgμ
a<gμm
a≥gμ
The correct Answer is:D
n=ma
fmax=μN=μma
μma≥mg
a≥gμ
Topper's Solved these Questions
Similar Questions
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θIn the given system, a block of mass m is resting on a board which makes an angle θ with the horizontal. What should be the minimum value of θ, so that the block just starts moving downwards? The coefficient of friction between the surfaces of the board and the block is μ.
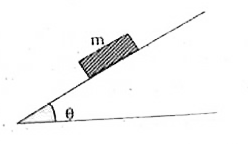 Atan−1(1/μ)Btan−1(μ)Csin−1μDnone
Atan−1(1/μ)Btan−1(μ)Csin−1μDnone
A rough vertical board has an acceleration a so that a 2 kg block pressing against it dows not fall. The coefficient of friction between the block and the board should beA>gaB<gaC=gaD>ag
Find out the distance travelled by the block as shown in figure. If the initial speed of the block is v and μ is the friction coefficient between the surface of block and ground.
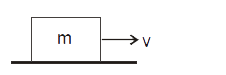
View SolutionFind the minimum value of F and the tension in the string so that the blocks move with constant velocity. The coefficient of friction at all surfaces is μ.
(a)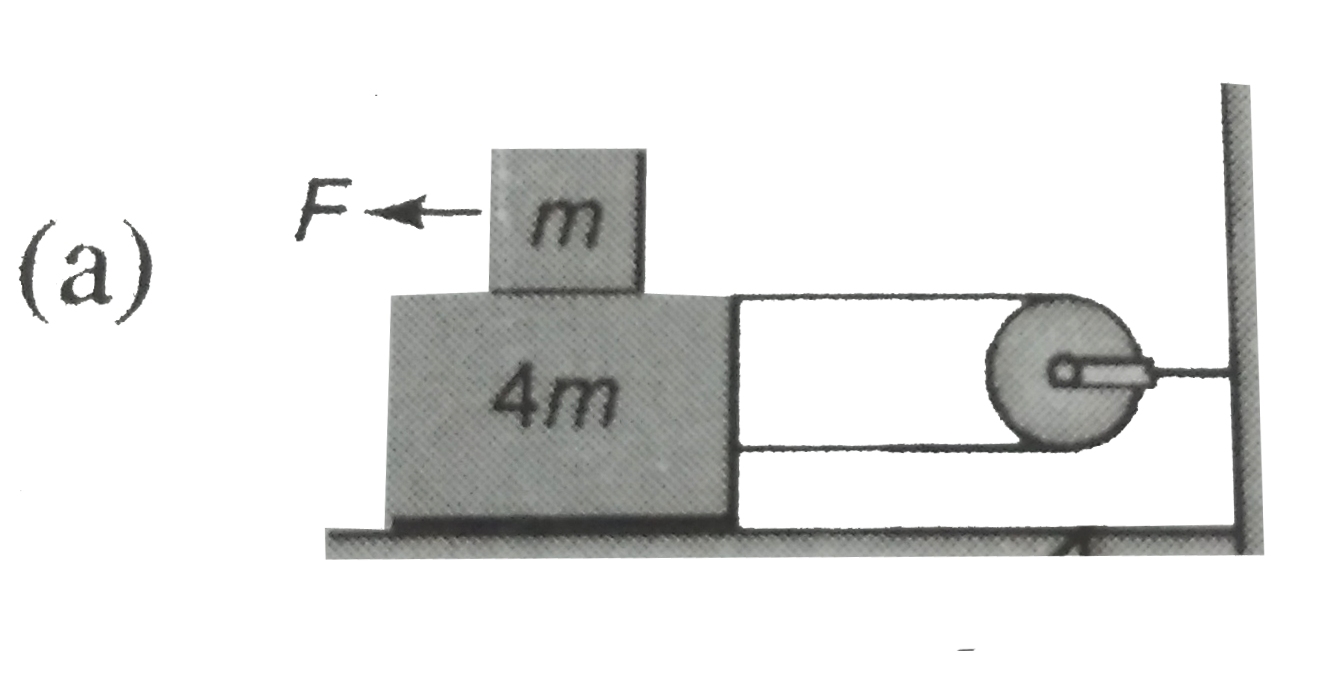
(b)
( c )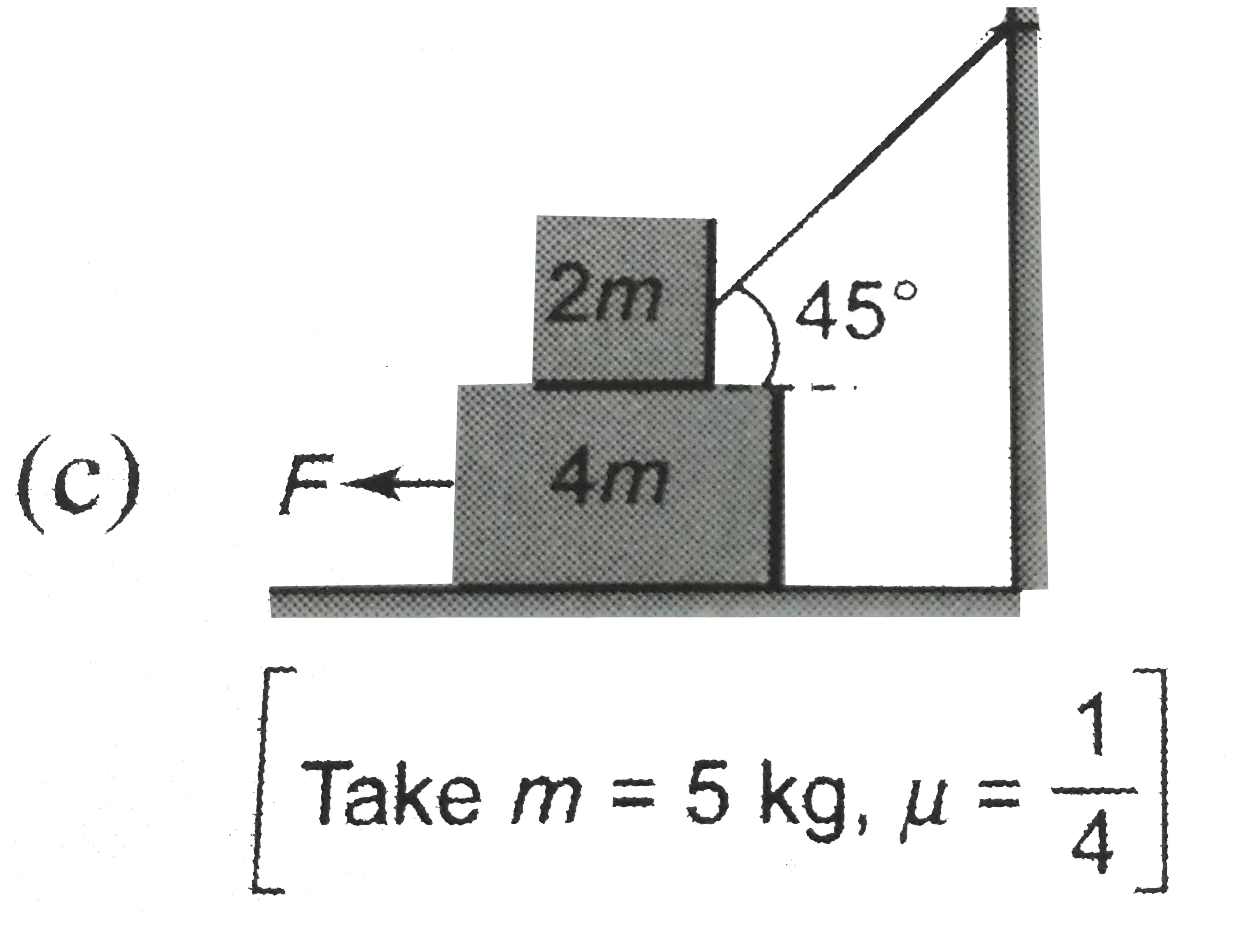
(d)
View SolutionAcceleration of block A varies with time as shown in figure the value of coefficient of kinetic friction between block A and B is
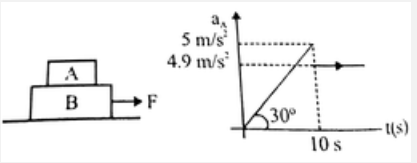
View SolutionA force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
View Solution
A block B is placed over a cart which in turn lies over a smooth horizontal floor. Block A and Block C are connected to block B with light inextensible strings passing over light frictionless pulleys fixed to the cart as shown. Initially the blocks and the cart are at rest. All the three blocks have mass m and the cart has mass M(M=3m). Now a constant horizontal force of magnitude F is applied to block A towards right.
Q. Let the coefficient of friction between block B and cart is μ(μ>0) and friction is absent everywhere else. Then the maximum value of force F applied to block A such that there is no relative acceleration between block B and cart is
View Solution

