The minimum strength of a uniform electric field which can tear a conducting uncharged thin-walled sphere into two parts is known to be E0. Determine the minimum electric field strength E1 required to tear the sphere of twice as large radius if the thickness ofits walls is the same as in the former case.
Step by step video & image solution for The minimum strength of a uniform electric field which can tear a conducting uncharged thin-walled sphere into two parts is known to be E_(0). Determine the minimum electric field strength E_(1) required to tear the sphere of twice as large radius if the thickness ofits walls is the same as in the former case. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Partice Exercise 1.11videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Partice Exercise93videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs33videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems107videos
GEOMETRICAL OPTICS
Similar Questions
Near an infinitely large flat plate with a surface charge density o on each side, the field strength is** E=δ∈nδ, while the field produced by a point charge at a distance r frorn the chargo is Prove that for a uniformly charged disk with a surface charge density a (on each side), the electric field strength on the axis of the disk is the same as for an infinitely large flat plate if the distances arc small in comparison with the disk's radius R, and is the same as for a point charge if the distances are large ** Usually the value of the field strength given in textbooks is half the one given here, since there it is assumed that the charge is on a geometric plane
View SolutionA current I, indicated by the crosses in fig. is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angles to the strip.
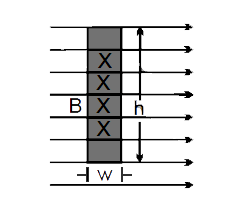
If no electric field is applied form the outside the electrons will be pushed somewhat to one side & thereforce will give rise to a uniform electric field EH across the conductor untill the force of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be magnitude and direction of the field EH? Assume that n, the number of conduction electrons per unit volume, is 1.1×1029/m3 & that h=0.02 meter, w=0.1cm, i=50 amp, & B=2webers/meter2.View Solution
Knowledge Check
- Question 1 - Select One
A uniform electric field in positive x-direction on exists in space. An uncharged solid conducting sphere is now placed in region of this uniform electric field. The centre of this sphere of radius R lies at origin. Then electric potential at any point on y−z plane (i.e. x=0 plane) due to only induced charged on surface of sphere.
Awill be positiveBwill be negativeCwill be zeroDmay be positive, zero or negative - Question 2 - Select One
Two concentric conducting thin shells of radius R and 2 R carry charges +Q and +3Q respectively. The magnitude of electric field at a distance x outside and inside from the surface of outer sphere is same. Then the value of x is
 AR3B2R3CR4DR2
AR3B2R3CR4DR2 - Question 3 - Select One
An insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0A(a) Statement 1 is true, Statement 2 is true, Statement 2 is not the correct explanation of statement 1.B(b) Statement 1 is true Statement 2 is false.C(c) Statement 1 is false Statement 2 is true.D(d) Statement 1 is true, Statement 2 is true, Statement 2 is the correct explanation of Statement 1
A hollow spherical conductor of radius R has a charge Q on it. A small dent on the surface decreases the volume of the spherical conductor by 2%. Assume that the charge density on the surface does not change due to the dent and the electric field in the dent region remains same as other points on the surface.
(a) ΔE is the electrostatic energy stored in the electric field in the shallow dent region and E is the total electrostatic energy of the spherical shell. Find the ratio ΔEE
(b) Using the ratio obtained in part (a) calculate the percentage change in capacitance of the sphere due to the dent.View SolutionIf x is measured from the centre of uniformly charged non-conducting sphere and a is radius of sphere the graph which best represents the variation of electric field (E) with x is E o a E
View SolutionA hollow charged sphere of radius R has a constant surface charge density o. Of the following graphs the one, which shows the variation of the electric field strength E with distance X from the centre of the sphere is (A) E I=R x (B) E 1
View SolutionAn electron accelerated by a potential difference V=3 volt first enters into a uniform electric field of a parallel plate capacitor whose plates extend over a length l=6cm in the direction of initial velocity. The electric field is normal to the direction of initial velocity and its strength varies with time as E=αt, where α=3600Vm−1s−1. Then the electron enters into a uniform magnetic field of induction B=π×10−9T. Direction of magnetic field is same as that of the electric field. Calculate pitch of helical path traced by the electron in the magnetic field. (Mass of electron, m=9×10−31kg)
View SolutionTwo large thin conducting plates with a small gap in between are placed in a uniform electric field E (perpendicular to the plates.)The area of each plate is A, and charges +Qand−Q are given to these plates as shown in figure. If R,S, and T are three points in space, then the
 View Solution
View Solution

