The mixture of a pure liquid and a solution in a along vertical column (i.e., horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d<<h, the height of the column.
Video Solution
Text Solution
In Fig. we have shown a ray of light entering the column at (x, y) at 90∘ to the vertical. A portion of ray between x and (x+dx) deviates through an angle dθ, emerging at (x+dx,y+dy) at angle (θ+dθ), while the angle at the entry is θ.
According to Snell's law,
μ(y)sinθ=μ(y+dy)sin(θ+dthη)
=[(μ(y)+dμdydy)](sinθcosdθ+cosθsindθ)
As dθ is small, cosdθ≈1 and sindθ=dθ.
∴μ(y)sinθ≈μ(y)sinθ+μ(y)cosθdθ+dμdydysinθ (fourth term is negligible small)
μ(y)cosθdθ=−dμdydysinθ
dθ=−1μdμdydytanθ
From Fig. tanθ=dxdyordytanθ=dx
dθ=−1μdμdydx
θ=−1μdμdy∫d0dx=−1μdμdy(d)
This is the required deviation in travelling a horizontal distance d.
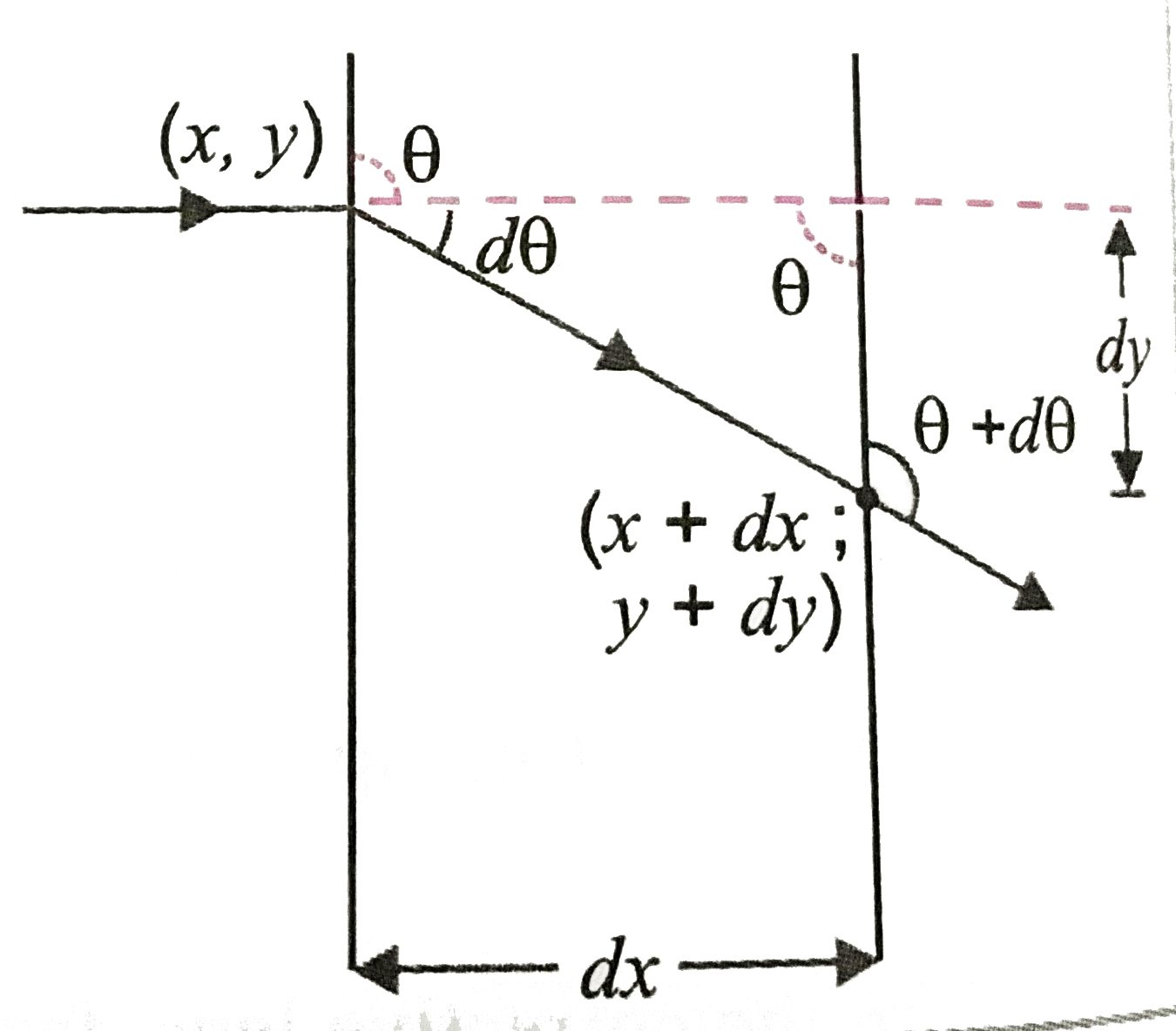
|
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Very short answer question
5 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - very short answer questions
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Knowledge Check
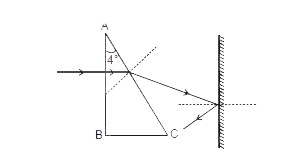
A prism having an apex angle 4∘ and refractive index 1.5 is located in front of a vertical plane mirror as shown in figure. Through what total angle is the ray is deviated after reflection from the mirror ?
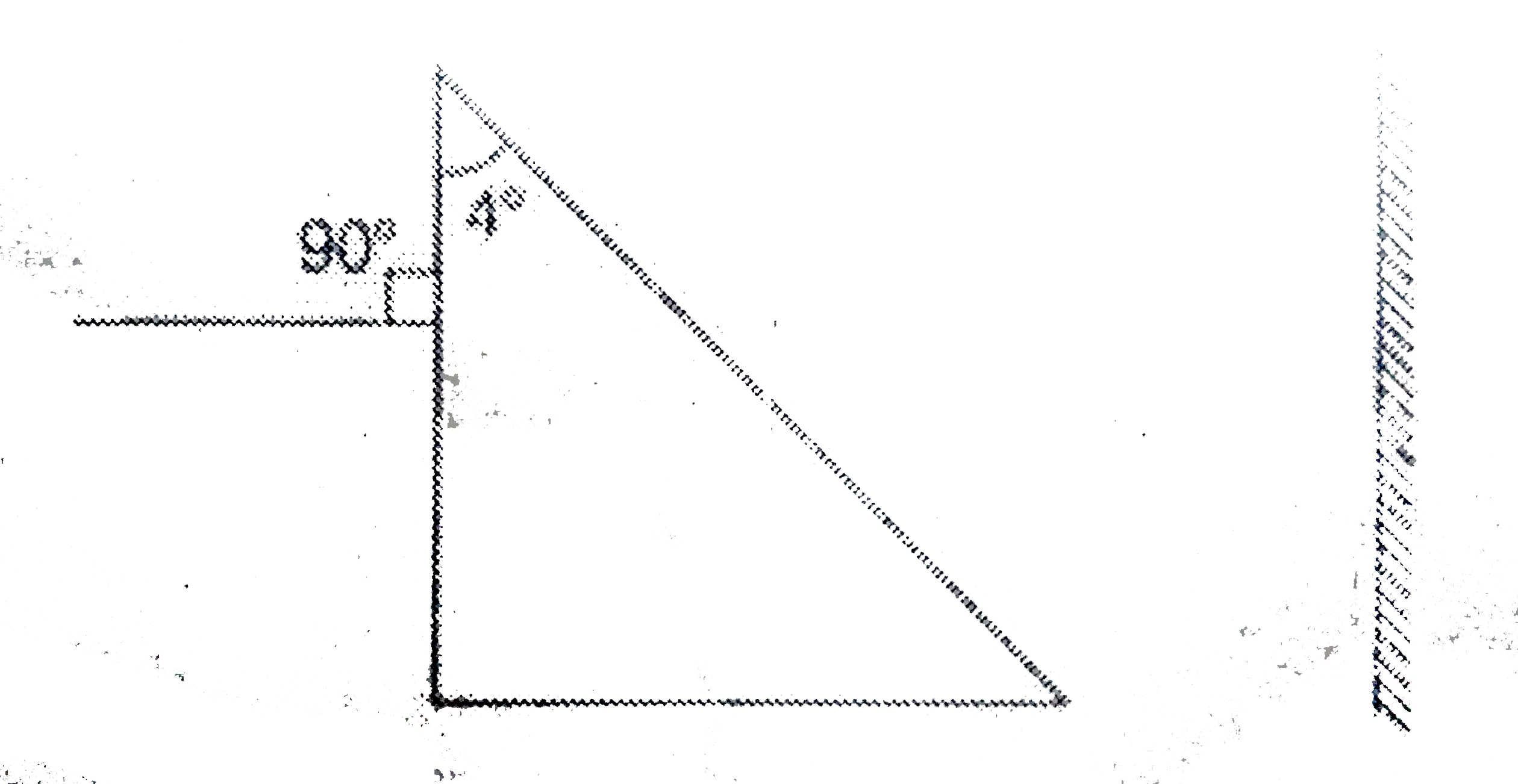 A176∘B4∘C178∘D2∘
A176∘B4∘C178∘D2∘A prism having an apex angle 4o and refraction index 1.5 is located in front of a vertical plane mirror as shown in figure. Through what total angle is the ray deviated after reflection from the mirror
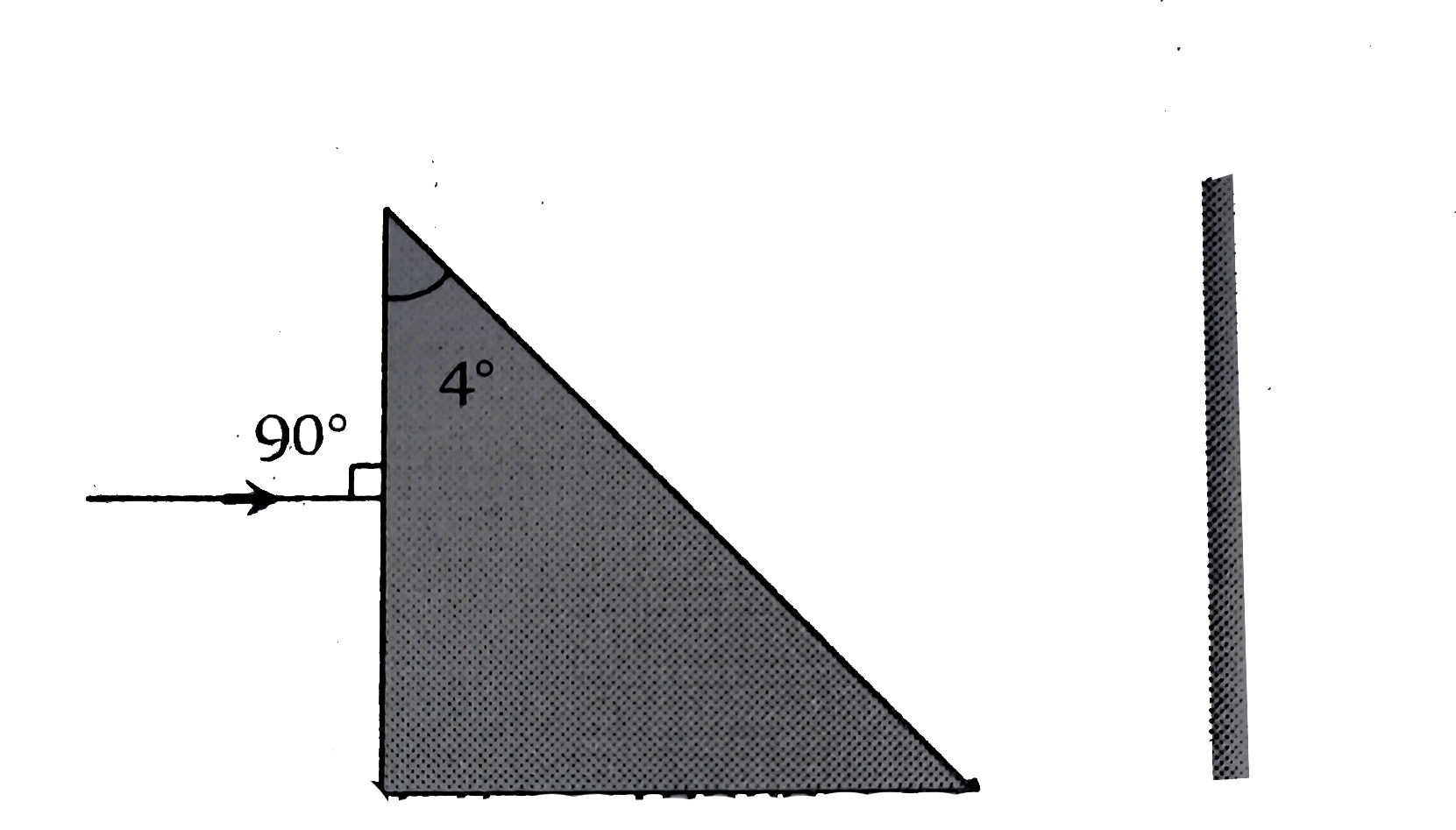 A176∘B4∘C178∘D2∘
A176∘B4∘C178∘D2∘The angle of a prism is 60∘ and its refractive index is √2 . The angle of minimum deviation suffered by a ray of light in passing through it is
AAbout 20∘B30∘C60∘D45∘
What are horizontal rows and vertical columns of the periodic table called ?
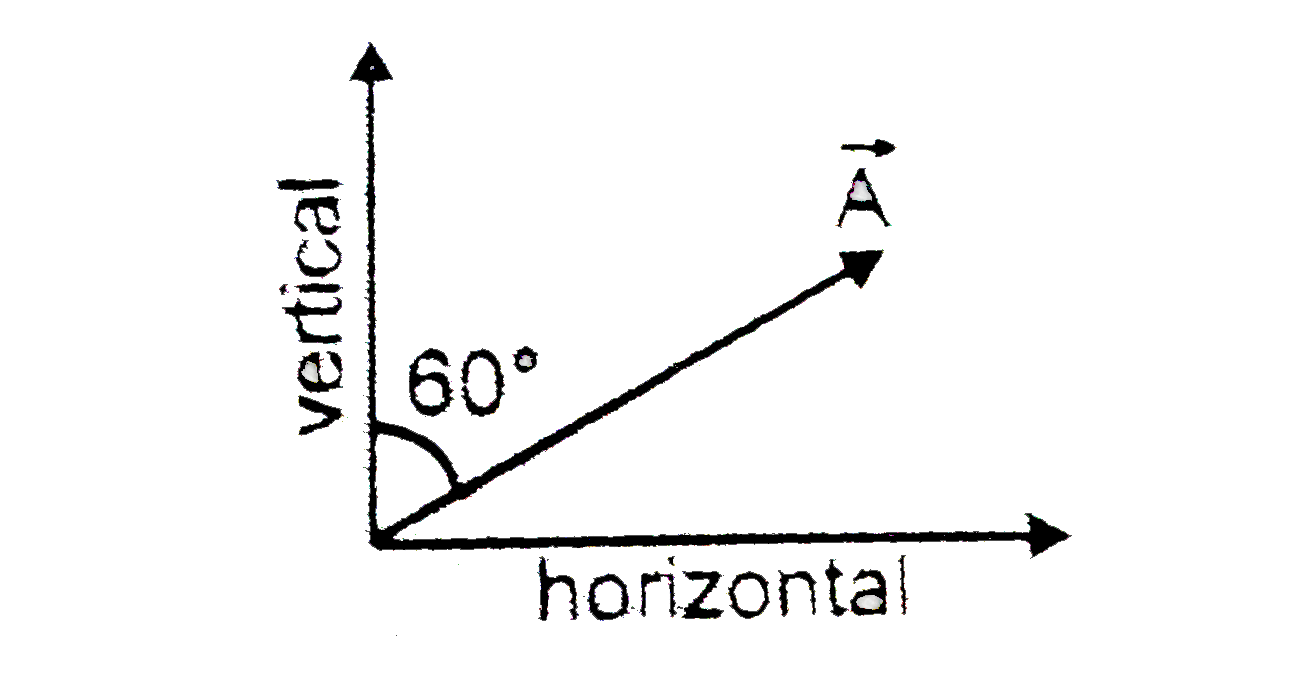
View SolutionA force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.
View SolutionA prism having a refracting angle 4∘ and refractive index 1.5 is located in front of a vertical plane mirror as shown. A horizontal ray of light is incident on the prism. What is the angle of incidence at the mirror ?
View SolutionA ray of light suffers a minimum deviation when incident on equilateral prism of refractive index √2 The angle of deviation is
View SolutionIf the angle (θ) between velocity vector and the acceleration vector of a moving particle is 90∘<θ<180∘, then the path of the particle is
View Solution
