The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
αIΔT
2αIΔT
αIΔT2
2IΔTα
The correct Answer is:B
To find the increase in the moment of inertia of a rod about its perpendicular bisector when the temperature is increased by ΔT, we can follow these steps:
1. Understand the Moment of Inertia:
The moment of inertia I of a rod about its perpendicular bisector is given by the formula:
I=112ml2
where m is the mass of the rod and l is its length.
2. Effect of Temperature on Length:
When the temperature of the rod increases by ΔT, the length of the rod changes due to thermal expansion. The change in length Δl can be expressed as:
Δl=αlΔT
where α is the coefficient of linear expansion of the material of the rod.
3. New Length of the Rod:
The new length l′ of the rod after the temperature increase is:
l′=l+Δl=l+αlΔT=l(1+αΔT)
4. Calculate the New Moment of Inertia:
The new moment of inertia I′ about the same axis (the perpendicular bisector) can be calculated using the new length:
I′=112m(l′)2=112m(l(1+αΔT))2
Expanding this:
I′=112m(l2(1+2αΔT+(αΔT)2))
Since (αΔT)2 is very small compared to 2αΔT, we can neglect it:
I′≈112ml2(1+2αΔT)=I(1+2αΔT)
5. Calculate the Increase in Moment of Inertia:
The increase in moment of inertia ΔI is given by:
ΔI=I′−I=I(1+2αΔT)−I=I(2αΔT)
Therefore, the increase in the moment of inertia is:
ΔI=2αIΔT
Final Answer:
The increase in the moment of inertia of the rod about its perpendicular bisector when the temperature is increased by ΔT is:
ΔI=2αIΔT
The moment of inertia I of a rod about its perpendicular bisector is given by the formula:
I=112ml2
where m is the mass of the rod and l is its length.
When the temperature of the rod increases by ΔT, the length of the rod changes due to thermal expansion. The change in length Δl can be expressed as:
Δl=αlΔT
where α is the coefficient of linear expansion of the material of the rod.
The new length l′ of the rod after the temperature increase is:
l′=l+Δl=l+αlΔT=l(1+αΔT)
The new moment of inertia I′ about the same axis (the perpendicular bisector) can be calculated using the new length:
I′=112m(l′)2=112m(l(1+αΔT))2
Expanding this:
I′=112m(l2(1+2αΔT+(αΔT)2))
Since (αΔT)2 is very small compared to 2αΔT, we can neglect it:
I′≈112ml2(1+2αΔT)=I(1+2αΔT)
The increase in moment of inertia ΔI is given by:
ΔI=I′−I=I(1+2αΔT)−I=I(2αΔT)
Therefore, the increase in the moment of inertia is:
ΔI=2αIΔT
The increase in the moment of inertia of the rod about its perpendicular bisector when the temperature is increased by ΔT is:
ΔI=2αIΔT
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Specific Heat Capacity
5 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Calorimetry
4 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Measurement Of Temperature
2 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Assertion And Reason
15 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
The moment of inertia of a rod about its perpendicular bisector is l, when temperature of rod is increased by ΔT, the increase in the moment of inertia of the rod about same axis (γ = temperature coefficient of volume expansion)
View SolutionCalculate the moment of inertia of the given rod about an axis CD
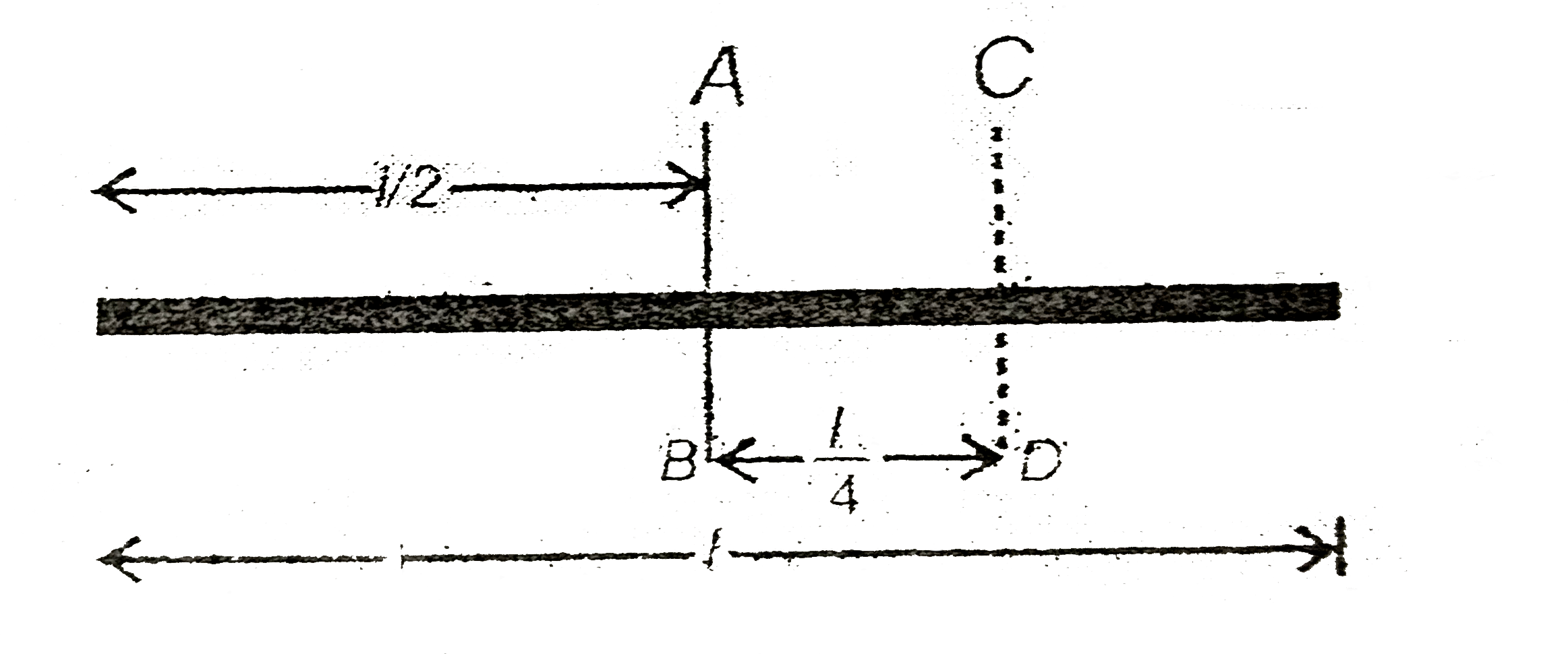
View Solution
Knowledge Check
The moment of ineratia of a uniform thin rod about its perpendicular bisector is I. If the temperature of the rod is increased by Δt , the moment of inertia about perpendicular bisector increases by (coefficient of linear expansion of material of the rod is α).
AZeroBIαΔtC2IαΔtDIαΔtWhen the temperature of a rod increases from t to t+Δt, its moment of inertia increases from I to I+ΔI. If α is coefficient of linear expansion, the value of ΔI/I is
A2αΔtBαΔtCαΔt/2DΔt/αMoment of inertia of a rod of mass 'M', length ? about an axis perpendicular to it through one end is,
AMl22,BMl23CMl212DNone of these
Calculate the moment of inertia of the given rod about an axis CD.
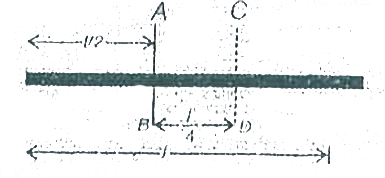
View SolutionIf l1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and l2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of I1 to I2 is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
View SolutionIf the temperature of a uniform rod is slightly increased by Δt, its moment of inertia I about a line parallel to itself will increased by
View SolutionThe diameter of a fly wheel is R. Its coefficient of linear expansion is α. If its temperature is increased by δT the percentage increase in its moment of inertia is
View Solution
