The nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge density ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
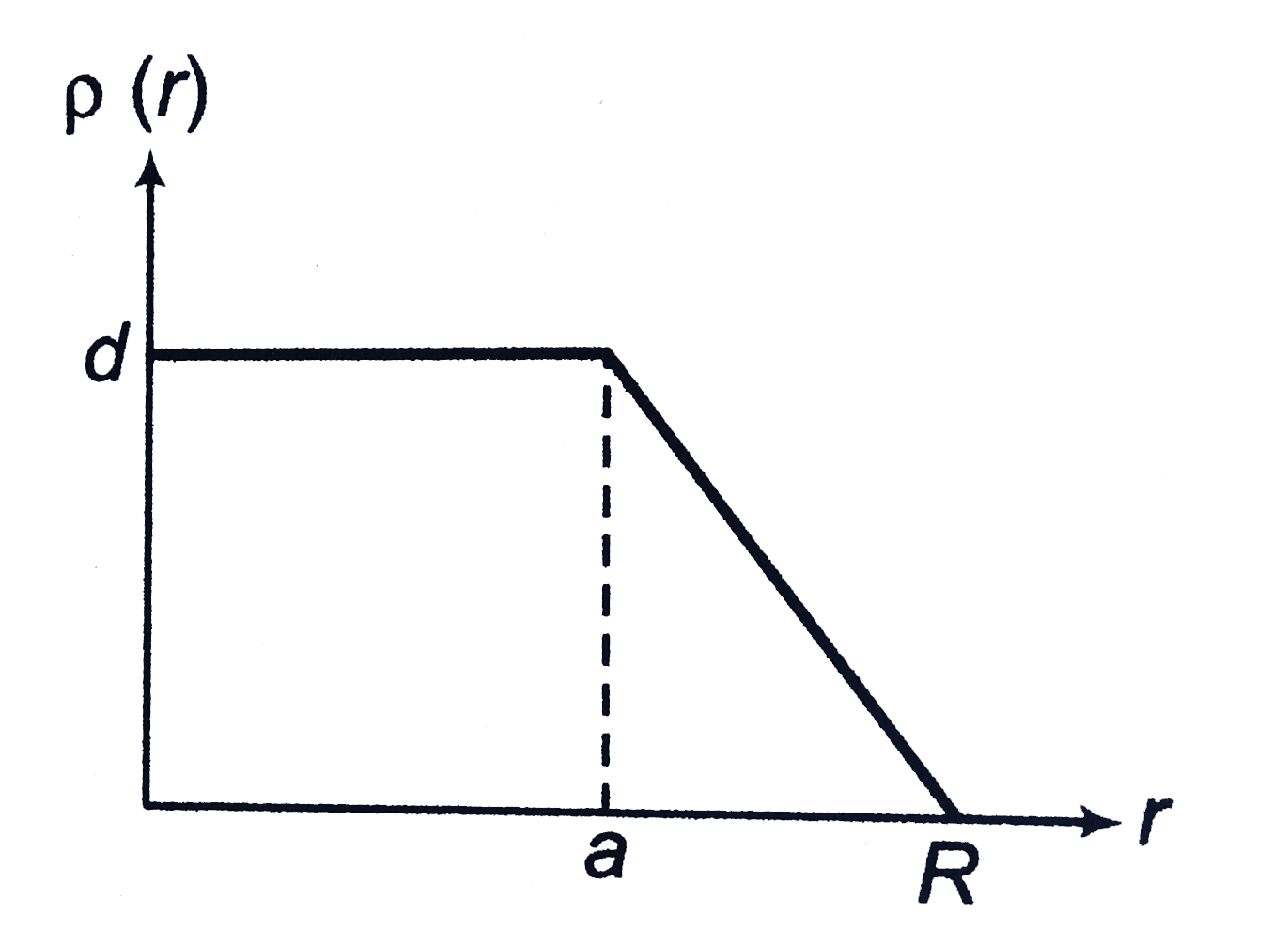
For a=0 the value of d (maximum value of ρ as shown in the figure) is
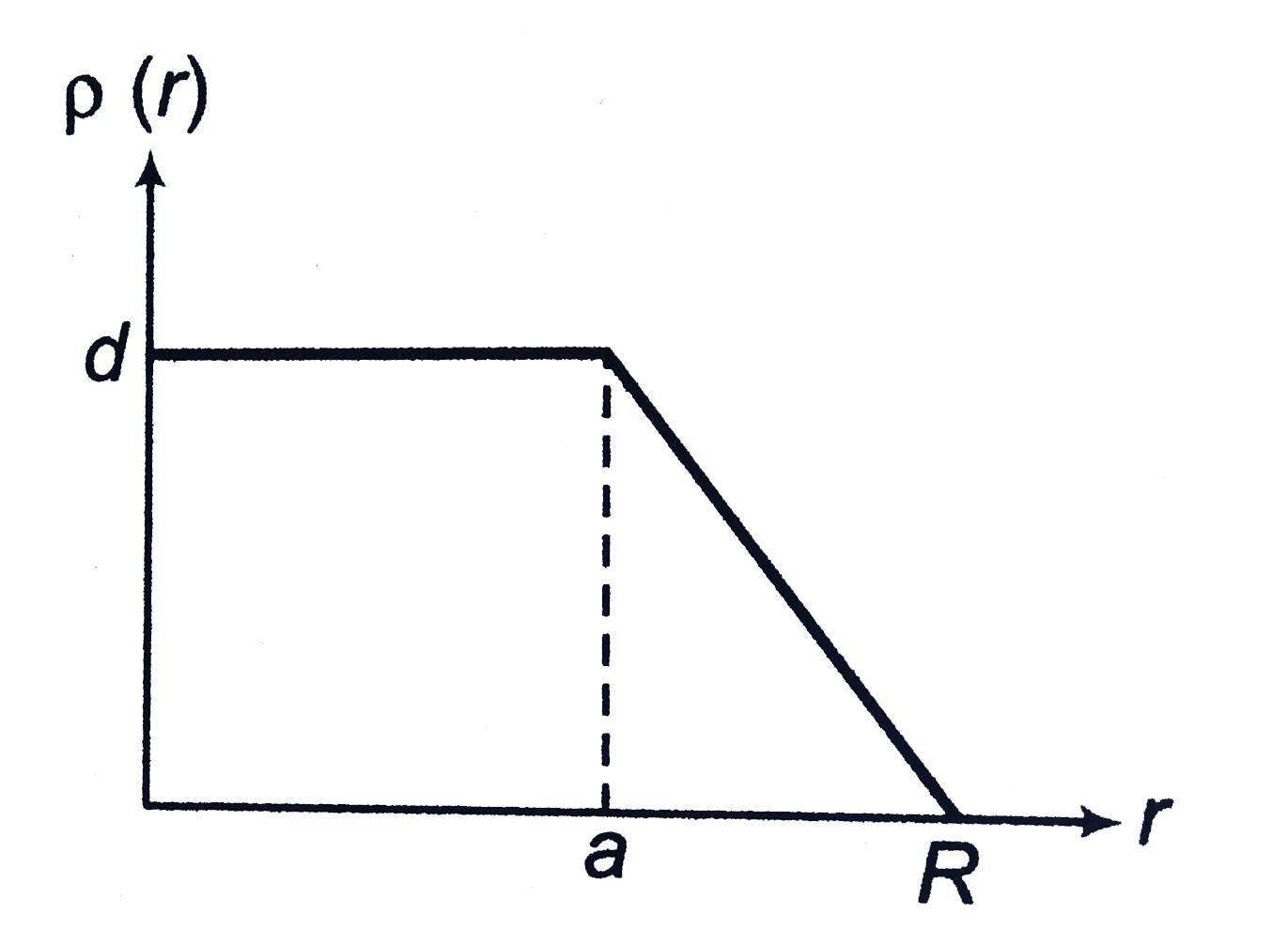
3Ze4πR3
3ZeπR3
4Ze3πR3
Ze3πR3
Net charge within r<R is constant, hence , electric field is independent of a.
q=∫R0dR(R−x)4πx2dx=Ze
d=3ZeπR3
if within a phere ρ is constant then E∝r
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Interger Answer type
Explore 20 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Fill in the blanks
Explore 10 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Assertion and Reason Type
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:CENGAGE PHYSICSChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Question Bank
Explore 4 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
Similar Questions
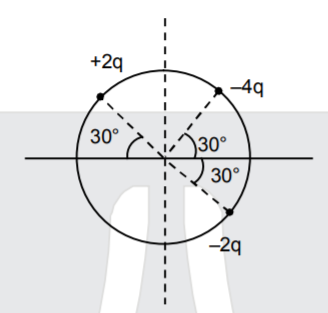
3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.
View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View Solution
Knowledge Check
The nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge density ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
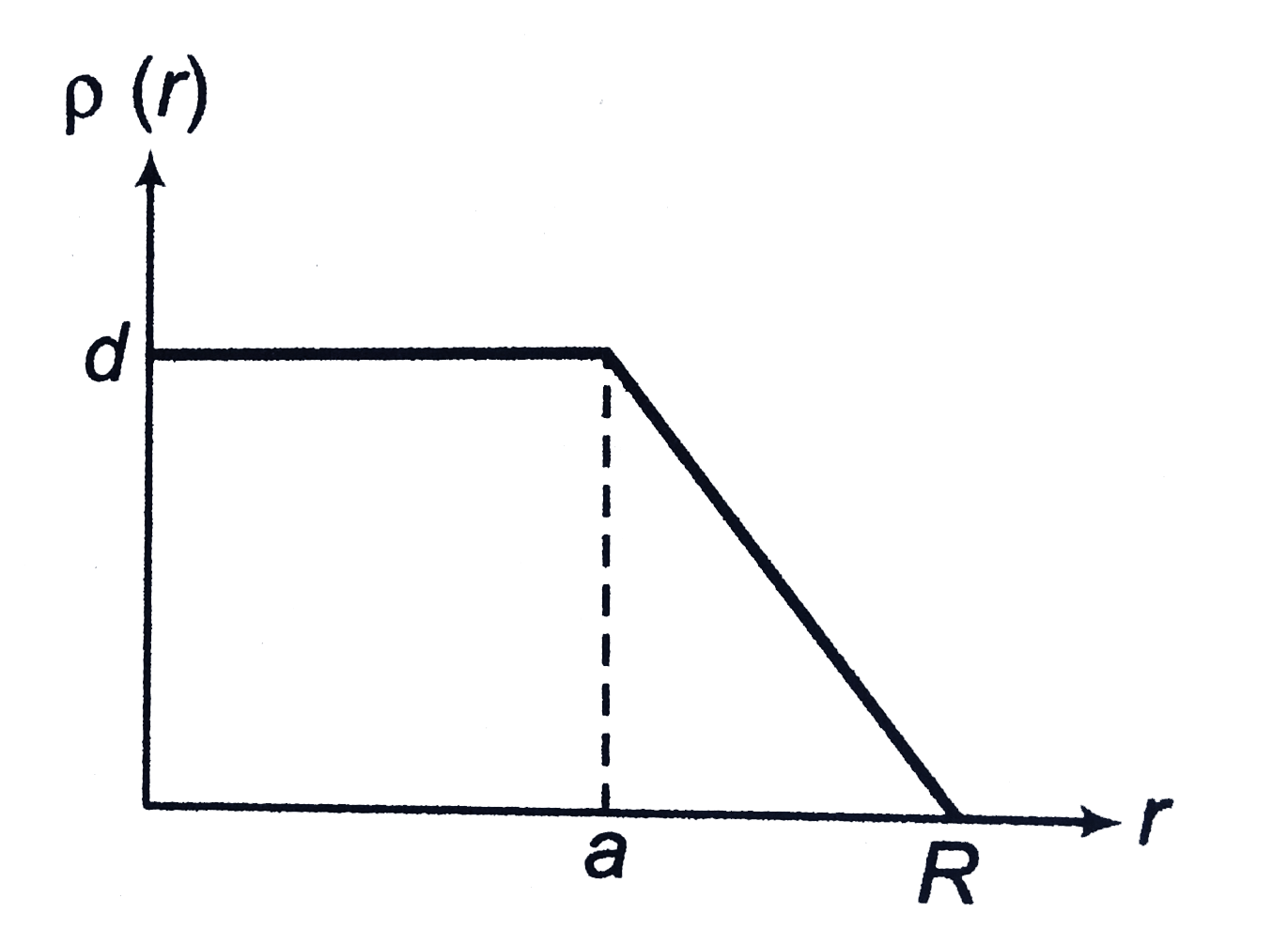
The electric field at r=R isAindependent of aBdirectly proportional to aCdirectly proportional to a2Dinversely proportional to a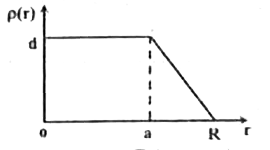
The electric field within the nucleus is generally observed to be linearly dependent on r. This implies.Aa=0Ba=R2Ca=RDa=2R3A solid sphere of radius R has a volume charge density ρ=ρ0r2 (where ρ0 is a constant ans r is the distance from centre). At a distance x from its centre (for x<R), the electric field is directly proportional to :
A1/x2B1/xCx3Dx2
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionThe volume charge density of a sphere carrying charge Q and of radius R is proportional to the square of the distance from the centre. The ratio of the magnitude of the electric field at a distance 2R from the centre to that at a distance of R2 from the centre is
View SolutionLet ρ(r)=QrπR4 be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
View SolutionInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
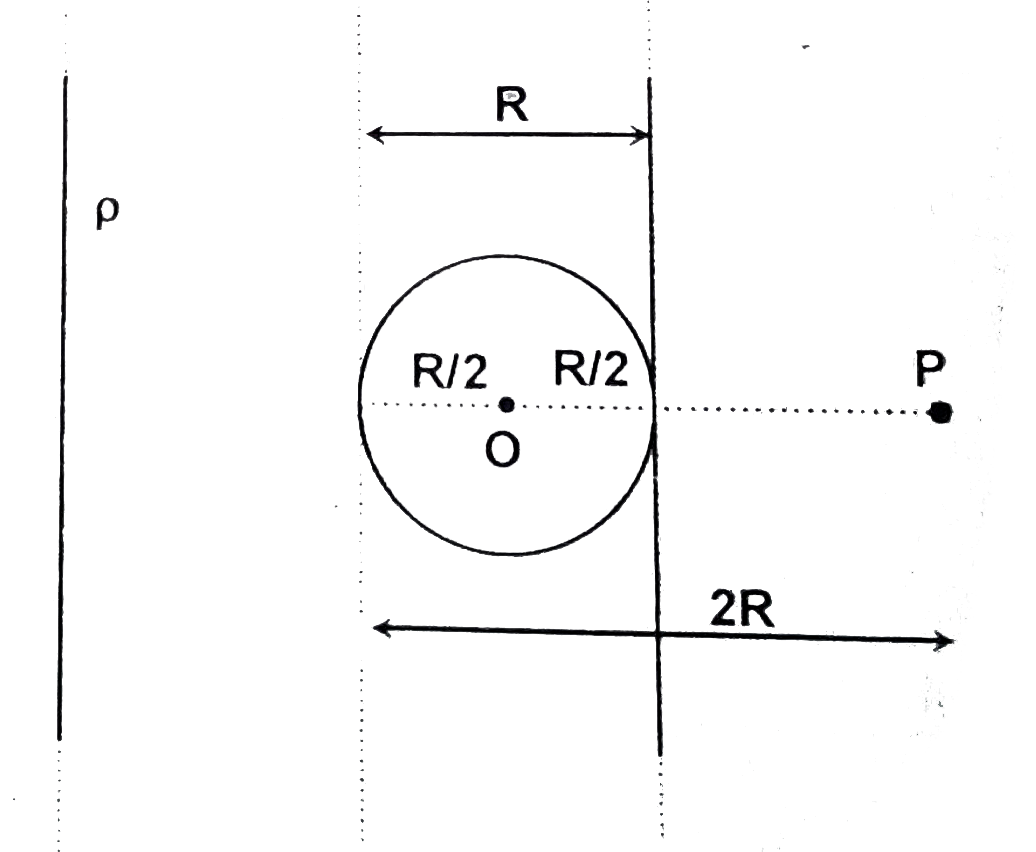
View SolutionLet ρ(r)=QrπR4 be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
View Solution