The number of beta particles emitter by radioactive sustance is twice the number of alpha particles emitter by it. The resulting daughter is an
isomer of parent
isotone of parent
isotope of parent
isobar of parent
The correct Answer is:c
To solve the problem, we need to analyze the emissions of alpha and beta particles from a radioactive substance and determine the nature of the resulting daughter nucleus.
1. Define the Parent Nucleus:
Let the parent nucleus be represented as X with mass number A and atomic number Z.
2. Identify Particle Emissions:
According to the problem, the number of beta particles emitted is twice the number of alpha particles emitted.
- Let the number of alpha particles emitted be n.
- Then, the number of beta particles emitted will be 2n.
3. Determine Changes in Mass and Atomic Numbers:
- Each alpha particle emission decreases the mass number by 4 and the atomic number by 2.
- Each beta particle emission does not change the mass number but increases the atomic number by 1 (since a beta particle is an electron emitted from the nucleus).
4. Calculate the Resulting Daughter Nucleus:
After emitting n alpha particles and 2n beta particles:
- The new mass number A′ will be:
A′=A−4n
- The new atomic number Z′ will be:
Z′=Z−2n+2n=Z
5. Analyze the Resulting Daughter Nucleus:
- The atomic number Z′ is equal to the original atomic number Z, which means the daughter nucleus has the same atomic number as the parent nucleus.
- Since the mass number has changed (decreased by 4n), the daughter nucleus is not an isobar (which would have the same mass number).
- The daughter nucleus is also not an isomer, as isomers have the same mass and atomic numbers but different energy states.
6. Conclusion:
Since the atomic number remains the same and the mass number has decreased, the resulting daughter nucleus is an isotope of the parent nucleus.
Final Answer:
The resulting daughter is an isotope of the parent nucleus.
Let the parent nucleus be represented as X with mass number A and atomic number Z.
According to the problem, the number of beta particles emitted is twice the number of alpha particles emitted.
- Let the number of alpha particles emitted be n.
- Then, the number of beta particles emitted will be 2n.
- Each alpha particle emission decreases the mass number by 4 and the atomic number by 2.
- Each beta particle emission does not change the mass number but increases the atomic number by 1 (since a beta particle is an electron emitted from the nucleus).
After emitting n alpha particles and 2n beta particles:
- The new mass number A′ will be:
A′=A−4n
- The new atomic number Z′ will be:
Z′=Z−2n+2n=Z
- The atomic number Z′ is equal to the original atomic number Z, which means the daughter nucleus has the same atomic number as the parent nucleus.
- Since the mass number has changed (decreased by 4n), the daughter nucleus is not an isobar (which would have the same mass number).
- The daughter nucleus is also not an isomer, as isomers have the same mass and atomic numbers but different energy states.
Since the atomic number remains the same and the mass number has decreased, the resulting daughter nucleus is an isotope of the parent nucleus.
The resulting daughter is an isotope of the parent nucleus.
Topper's Solved these Questions
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - HOTS
7 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - EXEMPLAR PROBLEMS
7 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
Similar Questions
What are the respective number of α and β-particles emitted in the following radioactive decay?
View SolutionA nucleus .mnX emits one α−particle and two β−particles. The resulting nucleus is
View SolutionA nucleus .nXm emits one α and one β particles. The resulting nucleus is.
View SolutionFrom a radioactive substance x numbers of α-particles any y numbers of β-particles are emitted. As a result atomic number decreases by n and mass number by m. Then, match the following two columns.
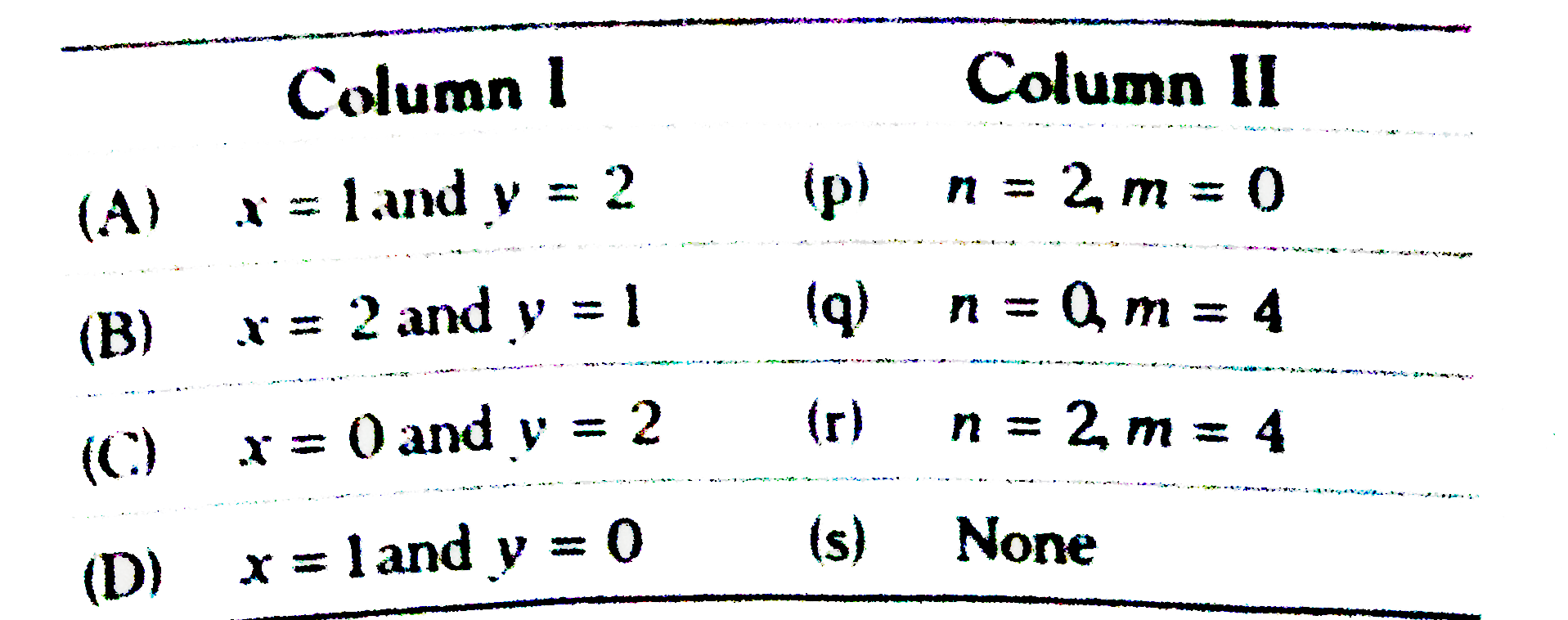
View SolutionWhen a β-particle is emitted by an atom of a radioactive element, the daughter nuclide formed possesses:
View SolutionHeavy radioactive nucleus decay through α−decay also. Consider a radioactive nucleus x. It spontaneously undergoes decay at rest resulting in the formation of a daughter nucleus y and the emission of an α− particle. The radioactive reaction can be given by
x→y+α
However , the nucleus y and the α− particle will be in motion. Then a natural question arises that what provides kinetic energy to the radioactive products. In fact, the difference of masses of the decaying nucleus and the decay products provides for the energy that is shared by the daughter nucleus and the α− particle as kinetic energy . We know that Einstein's mass-energy equivalence relation E=mc2. Let mx,my and mα be the masses of the parent nucleus x, the daughter nucleus y and α− particle respectively. Also the kinetic energy of α− particle just after the decay is E0. Assuming all motion of to be non-relativistic.
Which of the following is correct ?
View SolutionA radioactive element, U23892 undergoes successive radioactive decay and decays into Pb20682 The number of αandβ particles emitted respectively are
View SolutionWhen the nucleus of .238U92 disintegrates to give one nuclues of .206U82, the number of α− particles emitted and the number of β− particles emitted is
View SolutionHeavy radioactive nucleus decay through α−decay also. Consider a radioactive nucleus x. It spontaneously undergoes decay at rest resulting in the formation of a daughter nucleus y and the emission of an α− particle. The radioactive reaction can be given by
x→y+α
However , the nucleus y and the α− particle will be in motion. Then a natural question arises that what provides kinetic energy to the radioactive products. In fact, the difference of masses of the decaying nucleus and the decay products provides for the energy that is shared by the daughter nucleus and the α− particle as kinetic energy . We know that Einstein's mass-energy equivalence relation E=mc2. Let mx,my and mα be the masses of the parent nucleus x, the daughter nucleus y and α− particle respectively. Also the kinetic energy of α− particle just after the decay is E0. Assuming all motion of to be non-relativistic.
Just after the decy , if the speed of α− particle is v, then the speed of the centre of mass of the system of the daughter nucleud y and the α− particle will be
View SolutionA radioactive nuclide emitts γ- rays due to the :
View Solution
