The opposite faces of a cubical block of iron of cross-section 4 square cm are kept in contact with steam and melting ice. Calculate the quantity of ice melted at the end of 10 minutes. k for iron =0.2CGS units.
300g
150g
75g
450g
The correct Answer is:A
Let x be each side of the cube.
As area (A) of each face is 4cm2
A=x2=4cm2orx=2cm
Further, with usual notation,
(T1−T2)=(100−0)=100∘C
(T1 = temperature of steam, T2 = temperature of melting ice)
k=0.2CGS unit , t=10min=10×60s=600s
As, Q=KA(T1−T2)tx
Q=0.2×4×100×6002=24,000cal
if m gram of ice be melting with this heat and L be the latent heat of fusion of ice, Q=mL
Or, m=QL=2400080(asL=80cal/g)
or, m=300g.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion Reasoning
21 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - NEET Questions
47 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Transmission Of Heat : Radiation
28 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test
28 Videos
Similar Questions
One end of a copper rod of uniform cross-section and length 150 cm is in contact with ice and the other end with water at 100∘C . At what point along its length should a temperature of 200∘C be maintained so that in steady state, the mass of the ice melting is equal to that of steam produced in the same interval of time? Assume that whole system is insulated from the surroundings. Latent heat of steam =537calg−1 and lalent heat of fusion of ice =80calg−1.
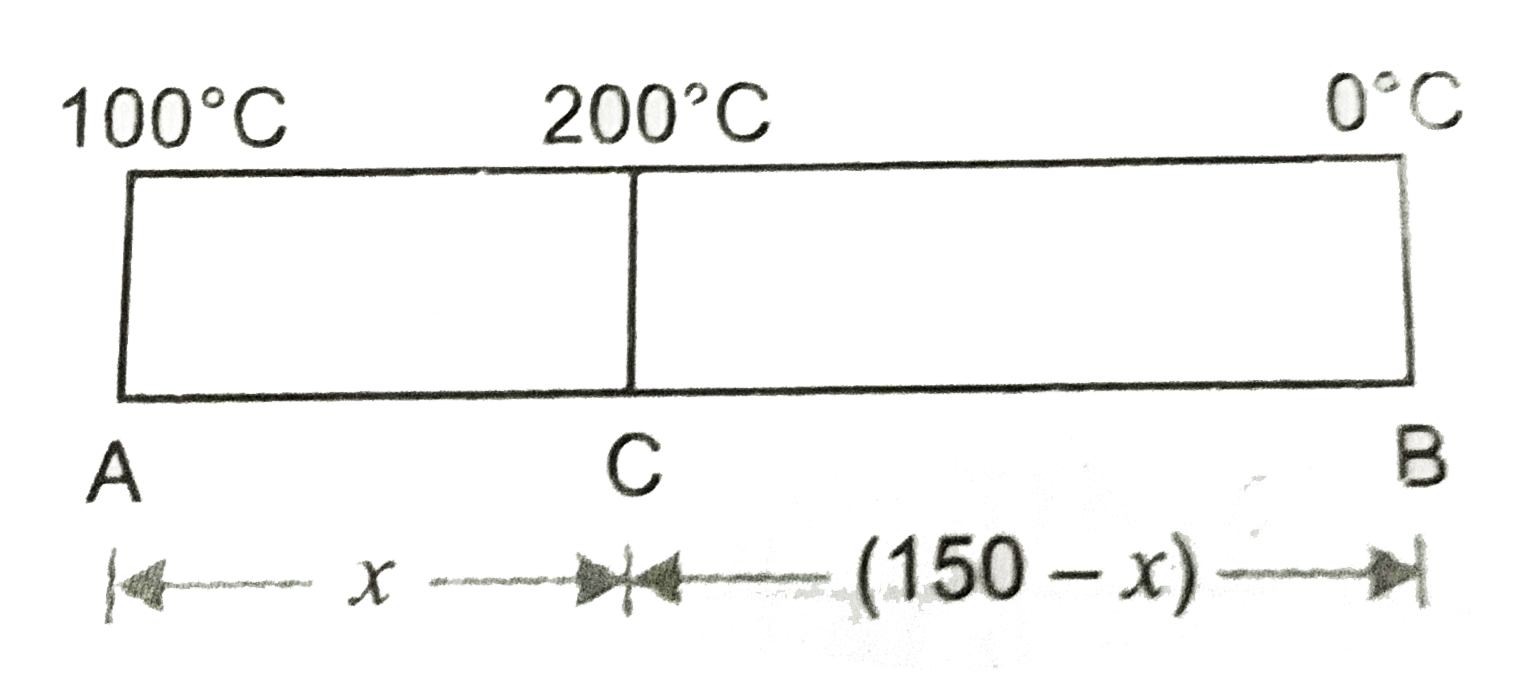 .
.
View SolutionA magnetising field of 1500A/m produces a flux of 2⋅4×10−5 weber in a bar of iron of cross-sectional area 0⋅5cm2. Calculate the permeability and susceptibility of the iron bar used.
View Solution
Knowledge Check
The two opposite faces of a cubical piece of iron (thermal conductivity = 0.2 CGS units) are at 100∘C and 0∘C in ice. If the area of a surface is 4cm2 , then the mass of ice melted in 10 minutes will b
A30 gmB300 gmC5 gmD50 gmOne end of metal bar of area of cross section 5cm2 and 25cm in length is in steam other in contact with ice, the amount of ice melts in one minute is (Lice=80cal/gm,K=0.8cgs uits) .
A16gmB12gmC24gmD36gmOne end of a copper rod of uniform cross section and length 1.5 m is kept in contact with ice and the other end with water at 100∘C. At what point along its length should a temperature of 200∘C be maintained so that in the steady state, the mass of ice melting be equal to that of the steam produced in same interval of time. Assume that the whole system is insulated from surroundings:
[Lice=80cal/g,Lsteam=540cal/g]A10.34 cm from the end at 100∘CB10.34 mm from the end at 100∘CC1.034 cm from the end at 100∘CD1.034 m from the end at 100∘C
One end of a uniform brass rod 20 cm long and 10cm2 cross-sectional area is kept at 100∘C. The other end is in perfect thermal contact with another rod of identical cross-section and length 10 cm. The free end of this rod is kept in melting ice and when the steady state has been reached, it is found that 360 g of ice melts per hour. Calculate the thermal conductivity of the rod, given that the thermal conductivity of brass is 0.25cal/scm∘CandL=80cal/g.
View SolutionThe lower surface of a slab of stone of face-area 3600cm^(2) and thickness 10cm is exposed to steam at 100∘C . A block of ice at 0^(@)C rests on the upper surface of the slab. 4.8g of ice melts in one hour. Calculate the thermal conductivity of the stone. Latent heat of fusion of ice =3.36xx10^(5) J kg^(-1)
View SolutionOne end of a copper rod of uniform cross-section and of length 3.1 m is kept in contact with ice and the other end with water at 100°C . At what point along it's length should a temperature of 200°C be maintained so that in steady state, the mass of ice melting be equal to that of the steam produced in the same interval of time. Assume that the whole system is insulated from the surroundings. Latent heat of fusion of ice and vaporisation of water are 80 cal/gm and 540 cal/gm respectively

View SolutionThe rays of the sun are focused on a piece of ice through a lens of diameter 5 cm , as a result of which 10g ice melts in 10 minutes. The amount of heat received from the sun per unit area per minute is
View SolutionIt takes 20 minutes to melt 10 g of ice, when ray from the sun are focused by a lens of diameter 5 cm on to a block of ice. Calcualate the heat received from the sun of 1cm2 per minute.
(Given, L = 80 kcal/kg)
View Solution