One end of a uniform brass rod 20 cm long and 10cm2 cross-sectional area is kept at 100∘C. The other end is in perfect thermal contact with another rod of identical cross-section and length 10 cm. The free end of this rod is kept in melting ice and when the steady state has been reached, it is found that 360 g of ice melts per hour. Calculate the thermal conductivity of the rod, given that the thermal conductivity of brass is 0.25cal/scm∘CandL=80cal/g.
The correct Answer is:A, B, C
L(dmdt)=TDR1+R2

or 80×3603600=100200.25×10+10K×10
Solving this equation, we get
K=0.222cal/cm−s−∘C.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 More Than One Correct5videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise13videos
BASIC MATHEMATICS
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
Similar Questions
One end of 0.5 m long metal rod is in steam at 100∘C and the other end is put in ice at 0∘C. If ice melts at the rate of 10 g/min, calculate the thermal conductivity of the metal. Take, cross sectional area of rod=2πcm2 . Latent ice of heat = 80 cal/g
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View Solution
Knowledge Check
- Question 1 - Select One
One end of a metal rod is dipped in boiling water and the other is dipped in melting ice.
Aall parts of the rod are in thermal equilibrium with each otherBwe can assign a temperature to the rodCwe can assign temperature to the rod after steady state is reached.Dthe state of the rod does not change after steady state is reached - Question 2 - Select One
One end of a metal rod is kept in a furnce. In steady state, the temperature of the rod
AincreasesBdecreasesCremains constantDis non uniform. - Question 3 - Select One
A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKL
One end of a 0.25 m long metal bar is in steam and the other is in contact with ice . If 12 g of ice melts per minute, what is the thermal conductivity of the metal? Given cross-section of the bar =5×10−4m2 and latent heat of ice is 80calg−1
View SolutionA metal rod of length 20 cm and diamter 2 cm is convered with a non conducting substance. One of its ends is maintained at 100∘C , while the other end is put at 0∘C. It is found that 25 g ice melts in 5 min. calculate the coefficient of thermal conductivity of the metal. Latent that of ice = 80calg−1.
View SolutionOne end of a uniform rod of mass M and cross-sectional area A is suspended from a rigid support and an equal mass M is suspended from the other end, what is the stress at the mid point of the rod.
View SolutionOne end of a brass rod of length 2.0 m and cross section 1cm2 is kept in stream at 100∘C and the other end in ice at 0∘C. The lateral suface of the rod is covered by heat insulator. Determine the amount of ice melting per minute. Thermal conductivity of brass is 110W/m−K and specific latent heat of fusion of ice is 80cal/g.
View SolutionTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
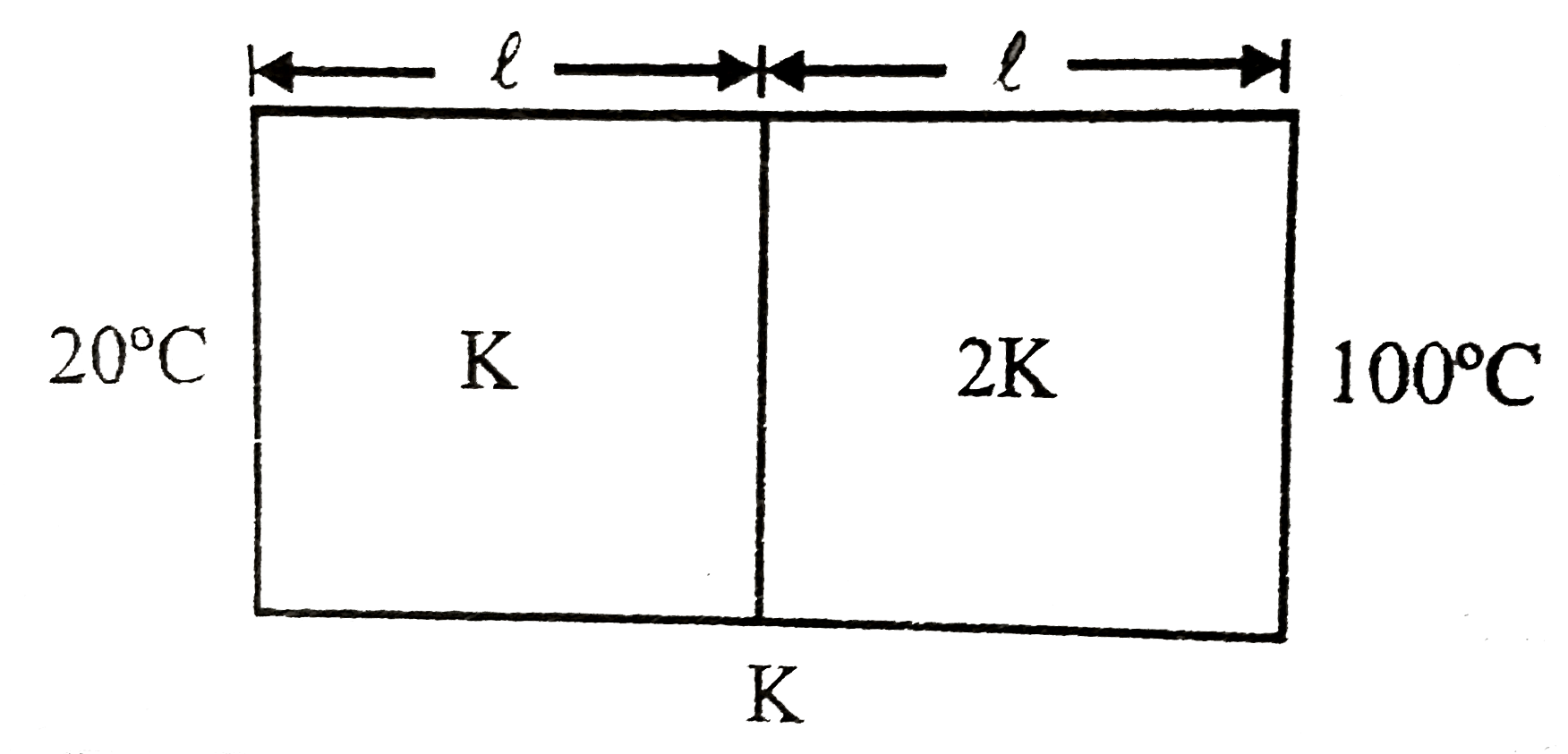 View Solution
View Solution

